

Next: 極、零点の配置と過渡応答
Up: 過渡応答
Previous: 一次遅れ要素の過渡応答
図 1.13:
sample系
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-3.eps} \end{center} \end{figure}](img219.png) |
ただし、
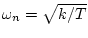 非減衰固有角周波数
非減衰固有角周波数
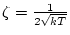 減衰係数
減衰係数
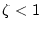 の場合、根
の場合、根
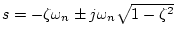
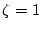 の場合、根
の場合、根 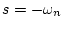
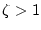 の場合、根
の場合、根
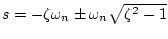
(a)インパルス応答
(i)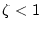 の場合
の場合
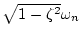 を固有角周波数という。
を固有角周波数という。
(ii)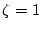 の場合
の場合
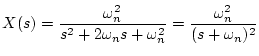 |
|
|
(1.62) |
![$\displaystyle x(t)={\cal L}^{-1}\left[ \frac{\omega _n^2}{(s+\omega _n)^2}\right]
=\omega _n^2te^{-\omega _nt}$](img238.png) |
|
|
(1.63) |
(iii)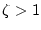 の場合
の場合
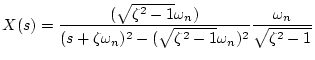 |
|
|
(1.64) |
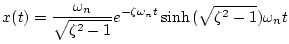 |
|
|
(1.65) |
図 1.14:
インパルス応答
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-4.eps} \end{center} \end{figure}](img241.png) |
(b)インディシャル応答
(i)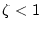 の場合
の場合
(ii)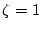 の場合
の場合
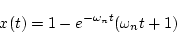 |
(1.68) |
(iii)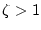 の場合
の場合
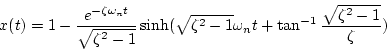 |
(1.69) |
図 1.15:
インディシャル応答
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-5.eps} \end{center} \end{figure}](img250.png) |
(c)単位ランプ応答
(i)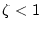 の場合
の場合
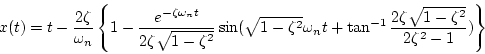 |
(1.70) |
(ii)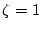 の場合
の場合
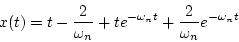 |
(1.71) |
(iii)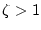 の場合
の場合
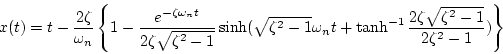 |
(1.72) |
図 1.16:
単位ランプ応答
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-6.eps} \end{center} \end{figure}](img254.png) |
(d)インディシャル応答の諸性質
(i)行き過ぎ量: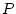
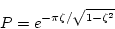 |
(1.73) |
(ii)振幅減衰比: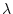
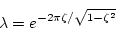 |
(1.74) |
(iii)行き過ぎ時間: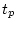
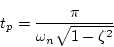 |
(1.75) |
(iv)整定時間: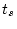
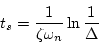 |
(1.76) |
図 1.17:
ステップ応答
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-7.eps} \end{center} \end{figure}](img267.png) |


Next: 極、零点の配置と過渡応答
Up: 過渡応答
Previous: 一次遅れ要素の過渡応答
Yasunari SHIDAMA
平成15年4月9日
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-4-3.eps} \end{center} \end{figure}](img219.png)
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]() の場合
の場合
![]()
![]()
![]()
![]()