極、零点の配置と過渡応答

（a）特性根と過渡応答

閉回路の過渡応答は（1.52）式より

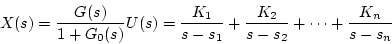$$X(s)=\frac{G(s)}{1+G_0(s)}U(s) =\frac{K_1}{s-s_1}+\frac{K_2}{s-s_2}+\cdots +\frac{K_n}{s-s_n}$$ (1.77)

､と書ける。この 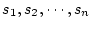$s_1,s_2,\cdots ,s_n$は

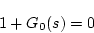$$1+G_0(s)=0$$ (1.78)

の根である。上式を特性方程式といい、この根を特性根という。特性根は一般に 複素根であり、その値、すなわち複素面上の根の位置によって過渡応答の 性質が定まる。

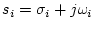$s_i=\sigma _i+j\omega _i$とした場合、根の位置と過渡応答の形の関係を 図1.18に示す。

図 1.18: 根の位置と過渡応答の形の関係

（b）極、零点のインディシャル応答に対する影響

閉回路のインディシャル応答は

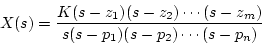$$X(s)=\frac{K(s-z_1)(s-z_2)\cdots (s-z_m)}{s(s-p_1)(s-p_2)\cdots (s-p_n)}$$ (1.79)

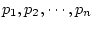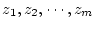で表される。この場合 $p_1,p_2,\cdots ,p_n$を極、 $z_1,z_2,\cdots ,z_m$を 零点という。この極と零点の配置がインディシャル応答に及ぼす影響は 次のごとくである。
i 20D 原点に近い極に対応する成分の係数が大きくなるのでこの極が インディシャル応答の大勢を決する。これを代表根（dominant root）という。
ii 20D 極の近くに零点があると、この極に対応する成分の係数は 小さくなる。
iii 20D 極と零点が近接していると、両者が打ち消しあって他の極には 影響を及ぼさない。

図 1.19: 極、零点の配置とインデンシャル応答