周波数応答とは

制御系に正弦波の入力信号を与え、出力信号が正弦波の定常状態に達したときの 応答を周波数応答という。

図 1.21: 周波数応答

正弦波入力の時

$$U(s)={\cal L}[e^{j\omega t}]=\frac{1}{s-j\omega }$$ (1.85)

とすると出力は

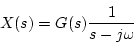$$X(s)=G(s)\frac{1}{s-j\omega }$$ (1.86)

となる。

$$x(t)={\cal L}^{-1}[X(s)] =e^{j\omega t}{\cal L}^{-1}[G(s+j\omega )\frac{1}{s}]$$ (1.87)

定常状態では

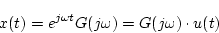$$x(t)=e^{j\omega t}G(j\omega )=G(j\omega )\cdot u(t)$$ (1.88)

となる。したがって、この場合の入出力の比は

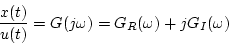$$\frac{x(t)}{u(t)}=G(j\omega )=G_R(\omega )+jG_I(\omega )$$ (1.89)

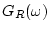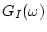となり、これを周波数伝達関数という。ただし$G_R(\omega )$は実数部、 $G_I(\omega )$は虚数部を表す。

周波数応答は次の２つの値によって表示する。

$$絶対値　M = \vert G(j\omega )\vert$$

$$= \sqrt{\{ G_R(\omega)\} ^2+\{ G_I(\omega)\} ^2}：ゲイン特性$$ (1.90)

$$偏角　　　\phi = \angle G(j\omega )$$

$$= \tan ^{-1}\{ G_I(\omega )/G_R(\omega )\} ：位相特性$$ (1.91)