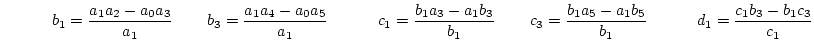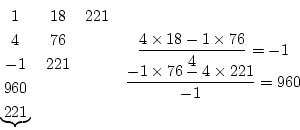

Next: Nyquistの安定判別法
Up: 安定判別
Previous: Hurwitzの安定判別法
これも特性方程式の根を求めずに安定の判別を行う方法で、前項の
Hurwitzの判別法と実質的には同じである。すなわち特性方程式が
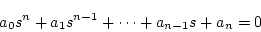 |
(1.100) |
のとき
(i)総ての係数
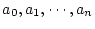 が存在し、かつ
同符号であり、
が存在し、かつ
同符号であり、
(ii)次の数列の第1列が総て同符号であれば、安定である。
ただし、
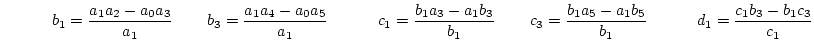
[例]前例と同じく、特性方程式が次式の場合
係数は総て存在し、かつ同符号ゆえ、次のRouthの数列を求めてみる。
符号の変化があるから不安定である。
注.第1列目に0がでた場合には、この項を正の微セ小量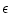 とおいて
以後の計算を続け符号の変化をみる。
とおいて
以後の計算を続け符号の変化をみる。
Yasunari SHIDAMA
平成15年4月9日