時間 ![]() の関数
の関数 ![]() があるとき、次の積分を
があるとき、次の積分を ![]() のラプラス変換とい
い、記号
のラプラス変換とい
い、記号
![]() で表す。
で表す。
【例】
通常はラプラス変換表を利用する。表1.2.1は自動制御理論において、 よく用いられる関数のラプラス変換表である。 ラプラス変換に際しては、表1.2.1に示される主要公式を適用する。
【例1】
![]() の初期値を
の初期値を![]() としてラプラス変換をすると
としてラプラス変換をすると
となる。
【例2】
上例において
![]() の時
の時
となる。この場合、最終値および初期値はそれぞれ、
により求められる。
【例3】
図1.5(a) に示す![]() は、同図(b)に示す
は、同図(b)に示す![]() と
と![]() の合
成として考えられる。
の合
成として考えられる。
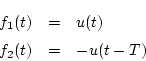
ゆえ
となる。
(注意:ラプラス変換をして ![]() の関数で表示した場合、
の関数で表示した場合、![]() の間は零で
の間は零で
![]() 以後現象が生じることを意味している)
以後現象が生じることを意味している)