

Next: ブロック線図
Up: 伝達関数とブロック線図
Previous: 伝達関数とブロック線図
伝達関数とは初期値をすべて零としたときの入出力のラプラス変換の比である。
伝達関数
![$[G(s)]
=\frac{\mbox{出力のラプラス変換}[X(s)]}{\mbox{入力のラプラス変換}[U(s)]}$](img162.png)
【例1】回転運動系
図 1.6:
回転運動系の例
![\begin{figure}\begin{center}
\psbox[scale=0.35]{eps/1-3-1.eps} \end{center} \end{figure}](img163.png) |
回転板の慣性モーメントを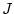 、回転角を
、回転角を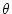 、角速度を
、角速度を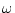 、軸受の
粘性減衰係数を
、軸受の
粘性減衰係数を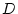 、加えたトルクを
、加えたトルクを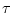 とすると
とすると
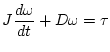 |
|
|
(1.45) |
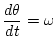 |
|
|
(1.46) |
の関係がある。両式を初期値を零としてラプラス変換をすると
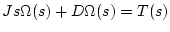 |
|
|
(1.47) |
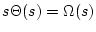 |
|
|
(1.48) |
になり、トルクを入力、回転角を出力とする伝達関数は
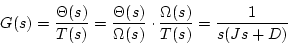 |
(1.49) |
となる。
自動制御系でよく用いられる伝達関数は表1.3.1のような基本形、
またはその組合わせである。
表 1.3:
伝達関数の基本形
| |
要素名 |
伝 達 関 数 |
| a |
比例要素 |
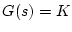 |
| b |
積分要素 |
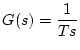 |
| c |
微分要素 |
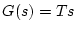 |
| d |
一次おくれ要素 |
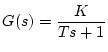 |
| e |
二次おくれ要素 |
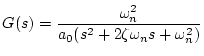 |
| f |
むだ時間要素 |
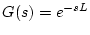 |
ただし、微分要素を単独で使用することは余りない。


Next: ブロック線図
Up: 伝達関数とブロック線図
Previous: 伝達関数とブロック線図
Yasunari SHIDAMA
平成15年4月9日
![]() 、回転角を
、回転角を![]() 、角速度を
、角速度を![]() 、軸受の
粘性減衰係数を
、軸受の
粘性減衰係数を![]() 、加えたトルクを
、加えたトルクを![]() とすると
とすると