

Next: 状態変数の変換法
Up: ベクトルおよびマトリックスによる表示
Previous: システムのベクトル表示
![\begin{displaymath}
\mbox{\boldmath$A$}=[a_{ij}]=
\left[\begin{array}{cccc}
a_{1...
...egin{array}{l}
\leftarrow 行(row)\\
\\
\\
\par\end{array}\end{displaymath}](img106.png) |
(2.47) |
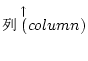
1列だけのとき
![\begin{displaymath}
\mbox{\boldmath$x$}=\left[\begin{array}{c}
x_1 x_2 \vdots x_n
\end{array}\right]
\end{displaymath}](img108.png) |
(2.48) |
 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
1 & 1 & 2\\
0 & 1 & 1\\
1 & 2 & 3
\end{array}\right]
\end{displaymath}](img115.png) |
(2.51) |
 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
1 & 2 & 7\\
2 & 4 & 13\\
7 & 13 & 0
\end{array}\right]
\end{displaymath}](img116.png) |
(2.52) |
対称行列のときは
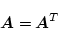 |
(2.53) |
対角行列(主対角線の両側がすべて0の対称行列)
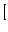 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
2 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -4
\end{array}\right]
\end{displaymath}](img118.png) |
(2.54) |
交代行列(Skew-symmetric)
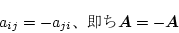 |
(2.55) |
の場合
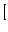 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
0 & 1 & -3\\
-1 & 0 & -2\\
3 & 2 & 0
\end{array}\right]
\end{displaymath}](img120.png) |
(2.56) |
対称行列を
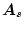 、交代行列を
、交代行列を
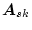 とした場合、正方行列
とした場合、正方行列
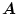 に対して次の関係がある。
に対して次の関係がある。
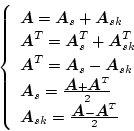 |
(2.57) |
 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{cc}
1 & 3\\
5 & 9
...
...]+
\left[\begin{array}{cc}
0 & -1\\
+1 & 0
\end{array}\right]
\end{displaymath}](img124.png) |
(2.58) |
![\begin{displaymath}
\mbox{\boldmath$I$}=
\left[\begin{array}{cccccc}
1 & 0 & 0 &...
...dots & 1 & 0 \\
0 & 0 & 0 & \cdots & 0 & 1
\end{array}\right]
\end{displaymath}](img125.png) |
(2.59) |
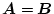 とは
とは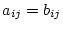 のこと。
のこと。
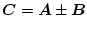 は
は
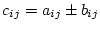
また
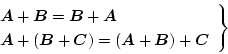 |
(2.60) |
 :スカラー、
:スカラー、
 :マトリックスとすると、
:マトリックスとすると、
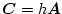 は
は
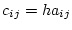
また
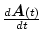 は
は
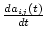
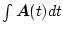 は
は
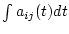
のことである。
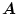 と
と
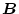 の積は
の積は
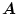 の列と
の列と
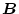 の行の数が等しいときのみ可能
の行の数が等しいときのみ可能
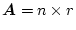 の行列、
の行列、
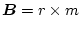 の行列のとき
の行列のとき
 の行列
の行列
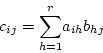 |
(2.61) |
 例
例![$]$](img114.png)
マトリックスの積に関する公式
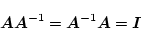 |
(2.66) |
の時
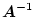 を逆行列(inverse matrix)という。但し
を逆行列(inverse matrix)という。但し
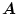 の行列式(determinant)
が零でない(正則行列)場合のみ存在する。
の行列式(determinant)
が零でない(正則行列)場合のみ存在する。
 |
(2.67) |
において、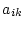 に対して
に対して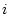 行
行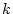 列を除いた行列式を小行列
列を除いた行列式を小行列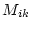 という。
という。
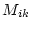 に
に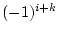 を掛けたものを
を掛けたものを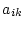 の余因子(cofactor)といい
の余因子(cofactor)といい
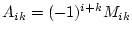 で表す。
で表す。
「逆行列
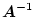 は、
は、
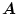 の成分
の成分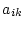 をその余因子
をその余因子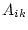 で置き換えてから転置行列を作り(これをadjoint matrixという)、それに
で置き換えてから転置行列を作り(これをadjoint matrixという)、それに
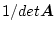 を掛けたものである。」
を掛けたものである。」
 例
例![$]$](img114.png)
![\begin{displaymath}
\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
8 & 4 & 2\\
2 & 8 & 4\\
1 & 2 & 8
\end{array}\right]
\end{displaymath}](img163.png) |
(2.68) |
の場合
になり、余因子は
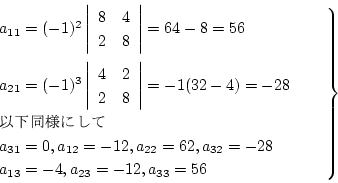 |
(2.70) |
となるので
| |
|
![$\displaystyle \mbox{\boldmath$A$}_{ik}=\left[\begin{array}{ccc}
56 & -12 & -4\\
-28 & 62 & -12\\
0 & -28 & 56
\end{array}\right]$](img169.png) |
(2.71) |
| |
|
![$\displaystyle \mbox{\boldmath$A$}_{ik}^T=\left[\begin{array}{ccc}
56 & -28 & 0\\
-12 & 62 & -28\\
-4 & -12 & 56
\end{array}\right]$](img170.png) |
(2.72) |
より逆行列は
| |
|
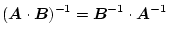 |
(2.74) |
| |
|
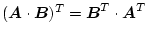 |
(2.75) |
| |
|
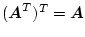 |
(2.76) |
| |
|
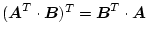 |
(2.77) |
| |
|
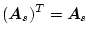 |
(2.78) |
| |
|
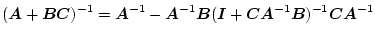 |
(2.79) |
| |
|
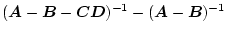 |
|
| |
|
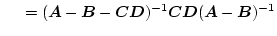 |
(2.80) |


Next: 状態変数の変換法
Up: ベクトルおよびマトリックスによる表示
Previous: システムのベクトル表示
Yasunari SHIDAMA
平成15年5月12日
![\begin{displaymath}
\mbox{\boldmath$A$}=[a_{ij}]=
\left[\begin{array}{cccc}
a_{1...
...egin{array}{l}
\leftarrow 行(row)\\
\\
\\
\par\end{array}\end{displaymath}](img106.png)
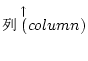
![]() 例
例![]()
![]() 例
例![]()
![]() は
は
![]()
![]() :スカラー、
:スカラー、
![]() :マトリックスとすると、
:マトリックスとすると、
![]() は
は
![]()
![]() は
は
![]()
![]() は
は
![]()
![]() と
と
![]() の積は
の積は
![]() の列と
の列と
![]() の行の数が等しいときのみ可能
の行の数が等しいときのみ可能
![]() の行列、
の行列、
![]() の行列のとき
の行列のとき
![]() の行列
の行列
![]() に
に![]() を掛けたものを
を掛けたものを![]() の余因子(cofactor)といい
の余因子(cofactor)といい
![]() で表す。
で表す。
![]() は、
は、
![]() の成分
の成分![]() をその余因子
をその余因子![]() で置き換えてから転置行列を作り(これをadjoint matrixという)、それに
で置き換えてから転置行列を作り(これをadjoint matrixという)、それに
![]() を掛けたものである。」
を掛けたものである。」
![]() 例
例![]()