


Next: 状態方程式の性質
Up: ベクトルおよびマトリックスによる表示
Previous: マトリックスの諸法則
任意の状態変数
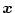 で表示されたシステムの状態方程式を
で表示されたシステムの状態方程式を
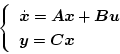 |
(2.81) |
とする。これを相変数の状態変数
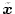 に変換するための
変換行列を
に変換するための
変換行列を
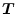 としたとき
としたとき
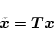 |
(2.82) |
で表わすことが出来る。ここに
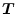 は
は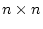 の行列で正則と
する。このとき
の行列で正則と
する。このとき
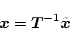 |
(2.83) |
ゆえ、(2.81)式に代入すると
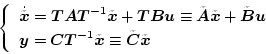 |
(2.84) |
となる。したがって
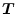 が求められれば任意の状態変数のシステムは
相変数表示に変換することができる。
が求められれば任意の状態変数のシステムは
相変数表示に変換することができる。
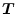 は次の手順で求めることができる。いま
は次の手順で求めることができる。いま
![\begin{displaymath}
\mbox{\boldmath$B$}=[\mbox{\boldmath$b$}_1,\mbox{\boldmath$b$}_2,\cdots ,\mbox{\boldmath$b$}_r]
\end{displaymath}](img189.png) |
(2.85) |
と分解し、次のマトリックスを作成する。但し、
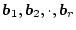 は一列のマトリックスである。
は一列のマトリックスである。
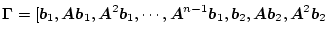 |
|
|
|
![$\displaystyle \cdots ,\mbox{\boldmath$A$}^{n-1}\mbox{\boldmath$b$}_2,\cdots ,\m...
...2\mbox{\boldmath$b$}_r,\cdots ,
\mbox{\boldmath$A$}^{n-1}\mbox{\boldmath$b$}_r]$](img192.png) |
|
|
(2.86) |
この複合マトリックスを次の順序に並びかえ
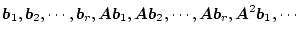
左から独立なベクトルを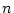 個とる。そして、そのベクトルだけを用いて再び
(2.86)式の順序に並べて
個とる。そして、そのベクトルだけを用いて再び
(2.86)式の順序に並べて
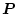 とする。すなわち
とする。すなわち
![\begin{displaymath}
\mbox{\boldmath$P$}=[\mbox{\boldmath$b$}_1,\mbox{\boldmath$A...
...dmath$b$}_r,
\mbox{\boldmath$A$}\mbox{\boldmath$b$}_r,\cdots ]
\end{displaymath}](img195.png) |
(2.87) |
とする。この
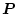 は正則であるから、逆行列をとって
は正則であるから、逆行列をとって
![\begin{displaymath}
\mbox{\boldmath$P$}^{-1}=
\left[\begin{array}{c}
e_{11} e...
... \vdots\\
\vdots \vdots \vdots d_r
\end{array}\right]
\end{displaymath}](img196.png) |
(2.88) |
とし、このうち下から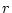 行をとって次の
行をとって次の
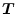 を作成すれば、それが
相変数への変換行列となる。
を作成すれば、それが
相変数への変換行列となる。
![\begin{displaymath}
\mbox{\boldmath$T$}=\left[\begin{array}{c}
d_1 d_1\mbox{\b...
... d_2\mbox{\boldmath$A$}^2\\
\vdots d_r
\end{array}\right]
\end{displaymath}](img197.png) |
(2.89) |
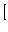 例
例![$]$](img114.png)
与えられた状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}=
\left[\begin{array}{cc}
1 & 3\\
...
...boldmath$x$}+
\left[\begin{array}{c}
1 1
\end{array}\right]u
\end{displaymath}](img198.png) |
(2.90) |
とする。このとき
![$
\mbox{\boldmath$A$}=
\left[\begin{array}{cc}
1 & 3\\
4 & 7
\end{array}\right]...
...ldmath$B$}=\mbox{\boldmath$b$}_1=\left[\begin{array}{c}1 1\end{array}\right]
$](img199.png) である。
である。
![$
\mbox{\boldmath$A$}\mbox{\boldmath$b$}_1=
\left[\begin{array}{cc}
1 & 3\\
4 &...
...ray}{c}1 1\end{array}\right]=
\left[\begin{array}{c}4 11\end{array}\right]
$](img200.png) ゆえ
ゆえ
![\begin{displaymath}
\mbox{\boldmath$P$}=[\mbox{\boldmath$b$}_1,\mbox{\boldmath$A...
...1]=
\left[\begin{array}{cc}
1 & 4\\
1 & 11
\end{array}\right]
\end{displaymath}](img201.png) |
(2.91) |
となり
![$
\mbox{\boldmath$P$}^{-1}=\frac{1}{7}
\left[\begin{array}{cc}
11 & -4\\
-1 & 1
\end{array}\right]
$](img202.png) から
から
が得られるので
![\begin{displaymath}
\mbox{\boldmath$T$}=
\left[\begin{array}{cc}
-\frac{1}{7} & \frac{1}{7}\\
\frac{3}{7} & \frac{4}{7}
\end{array}\right]
\end{displaymath}](img204.png) |
(2.92) |
となる。
![\begin{displaymath}
\mbox{\boldmath$T$}^{-1}=-7
\left[\begin{array}{cc}
\frac{4}...
...t]=
\left[\begin{array}{cc}
-4 & 1\\
3 & 1
\end{array}\right]
\end{displaymath}](img205.png) |
(2.93) |
であるから、相変数表示の
が得られる。
![\begin{displaymath}
\mbox{\boldmath$Y$}=\mbox{\boldmath$C$}\mbox{\boldmath$X$}=
...
...\begin{array}{cc}
1 & 0
\end{array}\right]
\mbox{\boldmath$X$}
\end{displaymath}](img211.png) |
(2.96) |
のとき
![\begin{displaymath}
\tilde{\mbox{\boldmath$C$}}=\mbox{\boldmath$C$}\mbox{\boldma...
...ray}\right]=
\left[\begin{array}{cc}
-4 & 1
\end{array}\right]
\end{displaymath}](img212.png) |
(2.97) |



Next: 状態方程式の性質
Up: ベクトルおよびマトリックスによる表示
Previous: マトリックスの諸法則
Yasunari SHIDAMA
平成15年5月12日
![]() で表示されたシステムの状態方程式を
で表示されたシステムの状態方程式を
![]() は次の手順で求めることができる。いま
は次の手順で求めることができる。いま
![$
\mbox{\boldmath$A$}=
\left[\begin{array}{cc}
1 & 3\\
4 & 7
\end{array}\right]...
...ldmath$B$}=\mbox{\boldmath$b$}_1=\left[\begin{array}{c}1 1\end{array}\right]
$](img199.png) である。
である。
![$
\mbox{\boldmath$A$}\mbox{\boldmath$b$}_1=
\left[\begin{array}{cc}
1 & 3\\
4 &...
...ray}{c}1 1\end{array}\right]=
\left[\begin{array}{c}4 11\end{array}\right]
$](img200.png) ゆえ
ゆえ
![$
\mbox{\boldmath$P$}^{-1}=\frac{1}{7}
\left[\begin{array}{cc}
11 & -4\\
-1 & 1
\end{array}\right]
$](img202.png) から
から
![\begin{eqnarray*}
\mbox{\boldmath$d$}_1=\frac{1}{7}
\left[\begin{array}{cc}
-1 &...
...ay}\right]=
\left[\begin{array}{cc}
3/7 & 4/7
\end{array}\right]
\end{eqnarray*}](img203.png)