


Next: 状態方程式の解
Up: 状態方程式の性質
Previous: 状態方程式から伝達関数の誘導
システムが
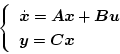 |
(2.118) |
で表示されたとき、ブロック線図は 図2.7 のように描かれる。
図 2.7:
システムのブロック線図
![\begin{figure}\begin{center}
\psbox[scale=0.40]{eps/2-4-1.eps} \end{center} \end{figure}](img255.png) |
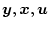 はベクトルであるから、それぞれは各変数を含んでいる。
従ってその中には実際に制御できるもの、あるいは観測できるものとできないもの
がある。ここに可制御性、可観測性の概念が生じる。
はベクトルであるから、それぞれは各変数を含んでいる。
従ってその中には実際に制御できるもの、あるいは観測できるものとできないもの
がある。ここに可制御性、可観測性の概念が生じる。
可制御性、可観測性の定義は次の如くである。
- 可制御性:
- ある制御入力
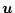 によって有限時間
によって有限時間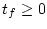 に
システムの初期状態
に
システムの初期状態
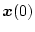 から、任意の最終状態
から、任意の最終状態
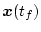 に到達できる
システムを可制御という。
に到達できる
システムを可制御という。
- 可観測性:
- 出力
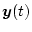 を有限時間
を有限時間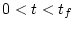 の間、観測することにより、
時刻
の間、観測することにより、
時刻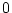 におけるすべての状態
におけるすべての状態
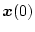 を求めることができるならば
可観測という。
を求めることができるならば
可観測という。
図 2.8:
システムの可制御、可観測の部分
![\begin{figure}\begin{center}
\psbox[scale=0.30]{eps/2-4-2.eps} \end{center} \end{figure}](img263.png) |
図2.8 の場合、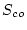 の部分は可制御、可観測であり、
の部分は可制御、可観測であり、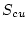 の部分は可制御、
不可観測、
の部分は可制御、
不可観測、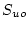 の部分は不可制御、可観測
の部分は不可制御、可観測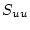 の部分は不可制御、
不可観測である。システム全体としては不可制御、不可観測となる。
の部分は不可制御、
不可観測である。システム全体としては不可制御、不可観測となる。
(2.118)式のシステムにおいて
- 次の
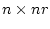 の複合マトリックスが
の複合マトリックスが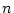 の階数(rank)であるときは
可制御である。
の階数(rank)であるときは
可制御である。
- 次の
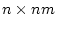 の複合マトリックスが
の複合マトリックスが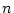 の階数(rank)であるときは
可観測である。
の階数(rank)であるときは
可観測である。
またシステムが次の単入力、単出力の場合は
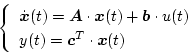 |
(2.119) |
- 次の
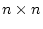 の複合マトリックスが正則であれば可制御、可観測
である。
の複合マトリックスが正則であれば可制御、可観測
である。
なおマトリックス
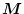 の階数とは、
の階数とは、
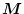 の中の行と列をいくつか
取り除いて作られる
の中の行と列をいくつか
取り除いて作られる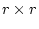 行列の行列式を
行列の行列式を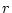 次の小行列式といい、
次の小行列式といい、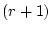 次の小行列式はすべて
次の小行列式はすべて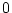 であるが、
であるが、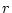 次の小行列式の中に
次の小行列式の中に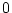 でないものがあるとき、
この
でないものがあるとき、
この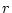 を指し
を指し
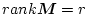 と書く。例えば
と書く。例えば
のとき
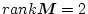 である。
である。
- 列の置換、および行の置換を行っても階数は変わらない。
- 1行または1列の全要素に同じ数を乗じても階数は変わらない。
- 1つの行(または列)にツ他の行(または列)の任意倍を加えても
階数は変わらない。
- 全部の要素が
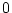 である行または列は除去しても階数は変わらない。
である行または列は除去しても階数は変わらない。
- 他の行(または列)の線形結合である行(または列)は除去しても
階数は変わらない。
 例
例![$]$](img114.png)
| |
|
![$\displaystyle \dot{\mbox{\boldmath$x$}}=
\left[\begin{array}{ccc}
-1 & 0 & 0 ...
...t]\mbox{\boldmath$x$}+
\left[\begin{array}{c}
1 1 0
\end{array}\right]u$](img281.png) |
(2.120) |
| |
|
![$\displaystyle y=\left[\begin{array}{ccc}
1 & 0 & 2
\end{array}\right]\mbox{\boldmath$x$}$](img282.png) |
|
の系の場合の可制御性、可観測性を判別する。
であるから
ゆえに
![\begin{displaymath}
\Bigl[\mbox{\boldmath$b$}\vert\mbox{\boldmath$A$}\mbox{\bold...
...{ccc}
1 & -1 & 1\\
1 & -2 & 4\\
0 & 0 & 0
\end{array}\right]
\end{displaymath}](img285.png) |
(2.121) |
この行列式は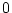 となり、特異行列であるから不可制御である。
となり、特異行列であるから不可制御である。
ゆえに
![\begin{displaymath}
\Bigl[\mbox{\boldmath$c$}\vert\mbox{\boldmath$A$}^T\mbox{\bo...
...ccc}
1 & -1 & 1\\
0 & 0 & 0\\
2 & -6 & 18
\end{array}\right]
\end{displaymath}](img287.png) |
(2.122) |
これも特異行列ゆえ不可観測である。
図 2.9:
システムのブロック線図
![\begin{figure}\begin{center}
\psbox[scale=0.40]{eps/2-4-3.eps} \end{center} \end{figure}](img288.png) |
この例はブロック線図に描くと 図2.9 の如くなり、#1ブロックは可制御
、可観測であるが、#2ブロックが可制御、不可観測であり#3不可制御、
可観測であるため全体として不可制御、不可観測となる。
もし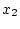 が#3の入力と接続されている場合は、全体として可制御、可観測
となる。
が#3の入力と接続されている場合は、全体として可制御、可観測
となる。



Next: 状態方程式の解
Up: 状態方程式の性質
Previous: 状態方程式から伝達関数の誘導
Yasunari SHIDAMA
平成15年5月12日
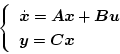
![]() はベクトルであるから、それぞれは各変数を含んでいる。
従ってその中には実際に制御できるもの、あるいは観測できるものとできないもの
がある。ここに可制御性、可観測性の概念が生じる。
はベクトルであるから、それぞれは各変数を含んでいる。
従ってその中には実際に制御できるもの、あるいは観測できるものとできないもの
がある。ここに可制御性、可観測性の概念が生じる。
![]() の部分は可制御、可観測であり、
の部分は可制御、可観測であり、![]() の部分は可制御、
不可観測、
の部分は可制御、
不可観測、![]() の部分は不可制御、可観測
の部分は不可制御、可観測![]() の部分は不可制御、
不可観測である。システム全体としては不可制御、不可観測となる。
の部分は不可制御、
不可観測である。システム全体としては不可制御、不可観測となる。
![]() の階数とは、
の階数とは、
![]() の中の行と列をいくつか
取り除いて作られる
の中の行と列をいくつか
取り除いて作られる![]() 行列の行列式を
行列の行列式を![]() 次の小行列式といい、
次の小行列式といい、![]() 次の小行列式はすべて
次の小行列式はすべて![]() であるが、
であるが、![]() 次の小行列式の中に
次の小行列式の中に![]() でないものがあるとき、
この
でないものがあるとき、
この![]() を指し
を指し
![]() と書く。例えば
と書く。例えば
![\begin{displaymath}\mbox{\boldmath$M$}=
\left[\begin{array}{cccc}
0 & 0 & 1 & 2\\
1 & 3 & 0 & 0\\
1 & 3 & 6 & 12
\end{array}\right] \end{displaymath}](img279.png)
![]() である。
である。
![]() 例
例![]()
![\begin{displaymath}\mbox{\boldmath$A$}=
\left[\begin{array}{ccc}
-1 & 0 & 0\\
0...
...h$c$}^T=
\left[\begin{array}{ccc}
1 & 0 & 2
\end{array}\right] \end{displaymath}](img283.png)
![\begin{eqnarray*}
&&\mbox{\boldmath$A$}\mbox{\boldmath$b$}=
\left[\begin{array}{...
...y}\right]=
\left[\begin{array}{c}
1 4 0
\end{array}\right]
\end{eqnarray*}](img284.png)
![\begin{eqnarray*}
&&\mbox{\boldmath$C$}=
\left[\begin{array}{c}
1 0 2
\end...
...math$c$}=
\left[\begin{array}{c}
1 0 18
\end{array}\right]
\end{eqnarray*}](img286.png)
![]() が#3の入力と接続されている場合は、全体として可制御、可観測
となる。
が#3の入力と接続されている場合は、全体として可制御、可観測
となる。