


Next: 最適制御理論
Up: 安定判別
Previous: 安定判別の考え方
いま二次系の場合のリアプノフ関数を
とする。これが正定であるための条件は
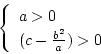 |
(2.153) |
である。いま上式を行列で表示すると
![\begin{displaymath}
V = \left [ \begin{array}{cc}
x_1 & x_2
\end{array} \right...
...
\left [ \begin{array}{c}
x_1 \\
x_2
\end{array} \right ]
\end{displaymath}](img384.png) |
(2.154) |
となり、正定の条件は次の如くなる。
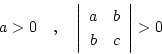 |
(2.155) |
一般的にリアプノフ関数を
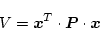 |
(2.156) |
但し
![\begin{displaymath}
\mbox{\boldmath$P$} = \left [ \begin{array}{cccc}
p_{11} & ...
... \\
p_{1n} & p_{2n} & \cdots & p_{nn}
\end{array} \right ]
\end{displaymath}](img387.png) |
(2.157) |
で表す。
正定の条件(Sylvester の条件)は次式で与えられる。
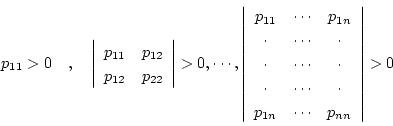 |
(2.158) |
自由系の場合
になるので、安定のための条件は
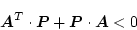 |
(2.162) |
となる。
通常安定判別を行うときは
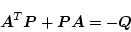 |
(2.163) |
とし、
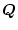 に適当な正の対角行列をとり、上式より
に適当な正の対角行列をとり、上式より
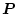 を求めて、それが
正定の条件を満足しておれば安定であると判定をする。
を求めて、それが
正定の条件を満足しておれば安定であると判定をする。
[例]図2.14 の系の場合
図 2.14:
sample系
![\begin{figure}\begin{center}
\psbox[scale=0.80]{eps/2-6-4.eps} \end{center} \end{figure}](img399.png) |
状態方程式は
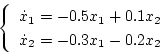 |
(2.164) |
であり、
![\begin{displaymath}
\left. \begin{array}{l}
\mbox{\boldmath$A$} = \left [ \begi...
...3 \\
0.1 & -0.2
\end{array} \right ]
\end{array} \right \}
\end{displaymath}](img401.png) |
(2.165) |
となる。
![$
\mbox{\boldmath$P$} = \left [ \begin{array}{cc}
p_{11} & p_{12} \\
p_{12} &...
...ldmath$Q$} = \left [ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right ]
$](img402.png) とすると、
とすると、
より
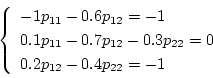 |
(2.167) |
になり
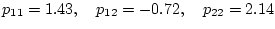 が得られる。正定の条件より
が得られる。正定の条件より
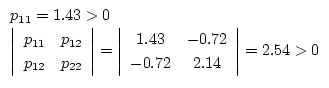 となるので、このシステムは安定である。
となるので、このシステムは安定である。
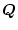 の選定は必ずしも単位行列とは限らず、計算が容易になるような適当な
対角行列にとる。
の選定は必ずしも単位行列とは限らず、計算が容易になるような適当な
対角行列にとる。
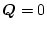 のときは持続振動となる。
のときは持続振動となる。



Next: 最適制御理論
Up: 安定判別
Previous: 安定判別の考え方
Yasunari SHIDAMA
平成15年5月12日
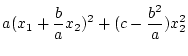
![$
\mbox{\boldmath$P$} = \left [ \begin{array}{cc}
p_{11} & p_{12} \\
p_{12} &...
...ldmath$Q$} = \left [ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right ]
$](img402.png) とすると、
とすると、
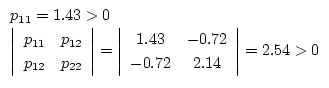 となるので、このシステムは安定である。
となるので、このシステムは安定である。
![]() の選定は必ずしも単位行列とは限らず、計算が容易になるような適当な
対角行列にとる。
の選定は必ずしも単位行列とは限らず、計算が容易になるような適当な
対角行列にとる。
![]() のときは持続振動となる。
のときは持続振動となる。