

Next: 最適制御法則
Up: 最適制御理論
Previous: 最終状態指定の場合
前項の方法を、より一般的にした場合であって、最終条件を指定せず評価の対象として
評価関数の中に含めるような形(Bolza形)にした場合である。
すなわち、![$S[x(t_f),t_f]$](img541.png) を最終条件の関数とし、評価関数を
を最終条件の関数とし、評価関数を
![\begin{displaymath}
J = \int^{t_f}_{t_i} L(\mbox{\boldmath$x$},\mbox{\boldmath$u$},t) d t + S[\mbox{\boldmath$x$}(t_f),t_f]
\end{displaymath}](img417.png) |
(2.230) |
とする。初期値
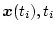 は指定されているので、上式第2項を
積分の中にいれ、それに全微分を適用すると、
は指定されているので、上式第2項を
積分の中にいれ、それに全微分を適用すると、
になる。この場合は、前項の(2.176)式の代りに、補助関数は
となる。
図 2.18:
![\begin{figure}\begin{center}
\psbox[scale=0.80]{eps/2-7-4.eps} \end{center} \end{figure}](img548.png) |
図2.18に示す如く、
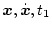 という軌道を通った場合と、
という軌道を通った場合と、
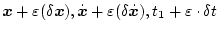 という軌道を通った場合の補助関数の差を
という軌道を通った場合の補助関数の差を
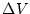 としたとき、これが0となる場合が極値となる。
としたとき、これが0となる場合が極値となる。
すなわち
となる。上式にTaylor展開を適用すると
のようになり、極値となる条件は
である。
上式の被積分関数の第2項に(2.182)式の部分積分を適用すると、
| |
![$\textstyle \int^{t_1}_{t_i} \left[ \frac{\partial L'}{\partial \mbox{\boldmath$...
... L'(\mbox{\boldmath$x$},\dot{\mbox{\boldmath$x$}},t) \cdot \delta t ]_{t = t_1}$](img565.png) |
|
|
| |
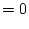 |
|
(2.233) |
となる。
2ー18図より
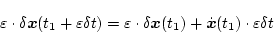 |
(2.234) |
の関係があり、かつ
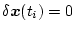 ゆえ(2.236)式は
ゆえ(2.236)式は
になる。
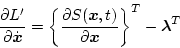 |
(2.236) |
ゆえ(2.238)式は
となる。
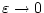 ゆえ、
ゆえ、
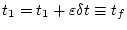 とし、かつ上式が任意の
とし、かつ上式が任意の
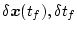 のとき
成立するには
のとき
成立するには
でなければならない。前者はオイラー方程式であり、後者は横断性
(Transervality Condition)の条件という。
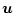 に関するオイラー方程式も前項と同様に成立するので
に関するオイラー方程式も前項と同様に成立するので
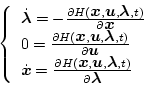 |
(2.239) |
の各式が成立する。
以上より、最適制御を求める手順としては、
(第1段階)
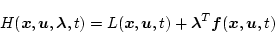 |
(2.240) |
を作る。
(第2段階)
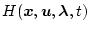 を最小にする
を最小にする
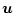 を求め、
を求め、
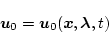 |
(2.241) |
とする。
(第3段階)
最適  関数
関数
 |
(2.242) |
を求める。
(第4段階)
| |
|
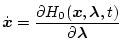 |
(2.243) |
| |
|
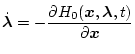 |
(2.244) |
を初期条件及び最終条件、又は次の横断性の条件によって解く。
![\begin{displaymath}
\left[ \left\{ \frac{\partial S(\mbox{\boldmath$x$},t)}
{\p...
...math$x$},t)}
{\partial t}
\right\}\delta t \right]_{t_f} = 0
\end{displaymath}](img588.png) |
(2.245) |
この場合、最終条件
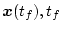 が指定されている場合は
が指定されている場合は
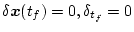 であり、また指定されていないときは
であり、また指定されていないときは
| |
|
![$\displaystyle \left[ \frac{\partial S(\mbox{\boldmath$x$},t)}{\partial \mbox{\boldmath$x$}} - \mbox{\boldmath$\lambda$}
\right]_{t_f} = 0$](img591.png) |
(2.246) |
| |
|
![$\displaystyle \left[ H_0(\mbox{\boldmath$x$},\mbox{\boldmath$\lambda$},t) + \fr...
...tial S(\mbox{\boldmath$x$},t)}
{\partial \mbox{\boldmath$x$}}
\right]_{t_f} = 0$](img592.png) |
(2.247) |
である。
(第5段階)
以上の結果を
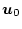 の式に代入して最適制御を得る。
の式に代入して最適制御を得る。
[例1]
システム方程式
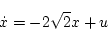 |
(2.248) |
評価関数
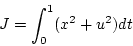 |
(2.249) |
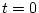 の時
の時 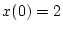 、最終時間
、最終時間 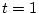 でその時の状態は自由とする。
でその時の状態は自由とする。
(第1段階)
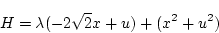 |
(2.250) |
(第2段階)
| |
|
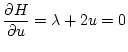 |
(2.251) |
| |
|
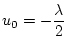 |
(2.252) |
(第3段階)
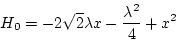 |
(2.253) |
(第4段階)
| |
|
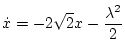 |
(2.254) |
| |
|
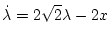 |
(2.255) |
両式より
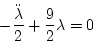 |
(2.256) |
解は
| |
|
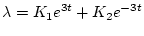 |
(2.257) |
| |
|
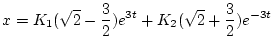 |
(2.258) |
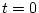 で
で 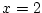 とすると
とすると
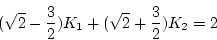 |
(2.259) |
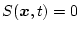 ゆえ(2.249)式より
ゆえ(2.249)式より
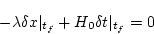 |
(2.260) |
最終時間が与えられているので 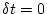
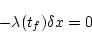 |
(2.261) |
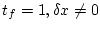 ゆえ
ゆえ
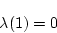 |
(2.262) |
(2.261)式に代入すると
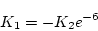 |
(2.263) |
(2.263)式に代入して
| |
|
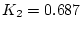 |
(2.264) |
| |
|
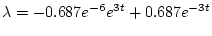 |
(2.265) |
(第5段階)
このとき
である。
[例2]
状態変数を
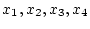 とし、評価関数が次のMeyer形とする。
とし、評価関数が次のMeyer形とする。
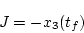 |
(2.269) |
この場合、最終時間 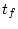 が規定されているとすると
が規定されているとすると 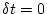 であり、かつ
であり、かつ
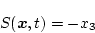 |
(2.270) |
ゆえ、横断性の条件は
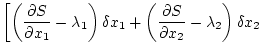 |
| |
|
![$\displaystyle + \left. \left. \left( \frac{\partial S}{\partial x_3} -\lambda_3...
...l S}{\partial x_4} -\lambda_4 \right)
\delta x_4 \right] \right\vert _{t_f} = 0$](img627.png) |
(2.271) |
すなわち
![\begin{displaymath}
\left. [ - \lambda_1 \delta x_1 - \lambda_2 \delta x_2
-(1 ...
...da_3)\delta x_3 -\lambda_4 \delta x_4 ] \right\vert _{t_f} = 0
\end{displaymath}](img628.png) |
(2.272) |
となる。
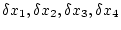 が任意のとき、
が任意のとき、
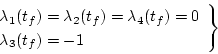 |
(2.273) |
であり、もし 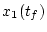 が指定されていると
が指定されていると
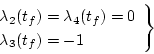 |
(2.274) |
さらに 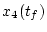 が指定されていると
が指定されていると
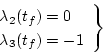 |
(2.275) |
が境界条件となる。
[例3]
システム方程式
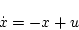 |
(2.276) |
評価関数
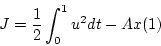 |
(2.277) |
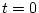 の時
の時 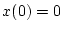 、最終時間
、最終時間 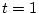 でその時の状態は自由とする。
でその時の状態は自由とする。
(第1段階)
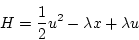 |
(2.278) |
(第2段階)
| |
|
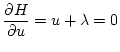 |
(2.279) |
| |
|
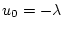 |
(2.280) |
(第3段階)
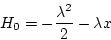 |
(2.281) |
(第4段階)
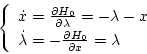 |
(2.282) |
両式より
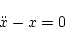 |
(2.283) |
解は
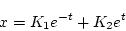 |
(2.284) |
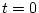 で
で 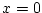 より
より
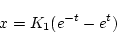 |
(2.285) |
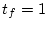 と指定されているから、
と指定されているから、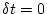 となり
となり
| |
|
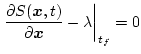 |
(2.286) |
| |
|
![$\displaystyle \left. \frac{\partial [ - A x ]}
{\partial \mbox{\boldmath$x$}} - \lambda \right \vert _{t_f}
= - A - \lambda \vert _{t_f} = 0$](img648.png) |
(2.287) |
| |
|
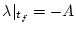 |
(2.288) |
| |
|
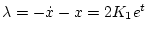 |
(2.289) |
| |
|
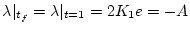 |
(2.290) |
| |
|
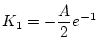 |
(2.291) |
| |
|
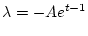 |
(2.292) |
(第5段階)
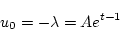 |
(2.293) |
が得られる。


Next: 最適制御法則
Up: 最適制御理論
Previous: 最終状態指定の場合
Yasunari SHIDAMA
平成15年5月12日
![]() を最終条件の関数とし、評価関数を
を最終条件の関数とし、評価関数を
![]() という軌道を通った場合と、
という軌道を通った場合と、
![]() という軌道を通った場合の補助関数の差を
という軌道を通った場合の補助関数の差を
![]() としたとき、これが0となる場合が極値となる。
としたとき、これが0となる場合が極値となる。
![]() に関するオイラー方程式も前項と同様に成立するので
に関するオイラー方程式も前項と同様に成立するので
![]() の式に代入して最適制御を得る。
の式に代入して最適制御を得る。
![]() とし、評価関数が次のMeyer形とする。
とし、評価関数が次のMeyer形とする。