

Next: リカッチの方法 (Riccati equation)
Up: 最適制御法則
Previous: 最適制御法則
前項の方法を発展させたもので、2点境界値問題を解かずに、閉回路として
最適制御方法を求める方法である。
システム方式を
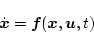 |
(2.294) |
評価関数を、
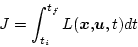 |
(2.295) |
とする。閉回路の最適制御方則を求める場合は、最適制御
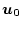 は
は
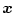 と
と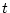 の関数となり、
の関数となり、
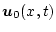 となる。
初期状態の時間を任意の
となる。
初期状態の時間を任意の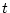 とし、最終時刻を
とし、最終時刻を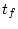 と固定して考える。その評価関数は、
と固定して考える。その評価関数は、
![\begin{displaymath}
V(\mbox{\boldmath$x$},t)=\int_{t}^{t_f}L\left[\mbox{\boldmat...
...ox{\boldmath$u$}_0(\mbox{\boldmath$x$},\tau),\tau\right]d \tau
\end{displaymath}](img659.png) |
(2.296) |
になり、上式を時間で微分すると、
![\begin{displaymath}
\dot{V}(\mbox{\boldmath$x$},t)=-L\left[\mbox{\boldmath$x$},\mbox{\boldmath$u$}_0(\mbox{\boldmath$x$},t),t\right]
\end{displaymath}](img660.png) |
(2.297) |
となる。一方
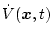 は全微分を適用すると、
は全微分を適用すると、
![\begin{displaymath}
\dot{V}(\mbox{\boldmath$x$},t)=\nabla \mbox{\boldmath$v$}^T(...
...$},t),t]
+\frac{\partial V(\mbox{\boldmath$x$},t)}{\partial t}
\end{displaymath}](img662.png) |
(2.298) |
但し、
![\begin{displaymath}
\nabla \mbox{\boldmath$v$}^T = [\frac{\partial V}{\partial x...
...artial V}
{\partial x_2}・・・\frac{\partial V}{\partial x_n}]
\end{displaymath}](img663.png) |
(2.299) |
と書ける。(2.301)式と(2.302)式より
![\begin{displaymath}
\nabla \mbox{\boldmath$v$}^T(\mbox{\boldmath$x$},t)\mbox{\bo...
...ldmath$x$},\mbox{\boldmath$u$}_0(\mbox{\boldmath$x$},t),t] = 0
\end{displaymath}](img664.png) |
(2.300) |
(2.304)式を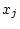 で偏微分すると
で偏微分すると
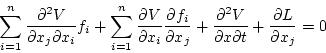 |
(2.301) |
一方
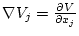 を時間で微分すると
を時間で微分すると
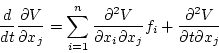 |
(2.302) |
(2.306)式を(2.305)式に代入すると
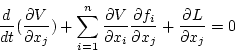 |
(2.303) |
(2.243),(2.186)式より
![\begin{displaymath}
\dot{\mbox{\boldmath$\lambda$}} = -\frac{\partial H_0(\mbox...
...ath$u$}_0,t) +
L(\mbox{\boldmath$x$},\mbox{\boldmath$u$}_0,t)]
\end{displaymath}](img670.png) |
(2.304) |
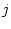 番目の要素は
番目の要素は
![\begin{displaymath}
\dot{\lambda}_j = -\left[\sum_{i=1}^{n}\lambda_i \frac{\par...
...x{\boldmath$x$},\mbox{\boldmath$u$}_0,t)}{\partial x_j}\right]
\end{displaymath}](img672.png) |
(2.305) |
(2.307),(2.309)式を比較して、もし
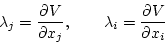 |
(2.306) |
とすれば両式は等しくなる。従って
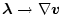 に置き換えると、(2.243)式の二番目の式は
に置き換えると、(2.243)式の二番目の式は
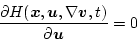 |
(2.307) |
になり、これより
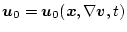 を求める。(2.186)
式は
を求める。(2.186)
式は
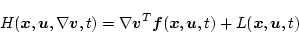 |
(2.308) |
と書かれ、(2.304)式は
![\begin{displaymath}
\nabla \mbox{\boldmath$v$}^T (\mbox{\boldmath$x$},t)\mbox{\...
...h$u$}_0(\mbox{\boldmath$x$},\nabla \mbox{\boldmath$v$},t),t]=0
\end{displaymath}](img678.png) |
(2.309) |
と書かれる。従って
のようになるから、(2.313) (2.314)式より
![\begin{displaymath}
H_0[\mbox{\boldmath$x$},\nabla \mbox{\boldmath$v$}(\mbox{\b...
...t] + \frac{\partial V(\mbox{\boldmath$x$},t)}{\partial t}
= 0
\end{displaymath}](img682.png) |
(2.310) |
になる。これがハミルトン・ヤコビ
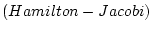 方程式である。
以上より最適制御法則を求める手順としては
方程式である。
以上より最適制御法則を求める手順としては
(第1段階)
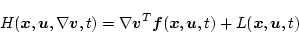 |
(2.311) |
を作る。
(第2段階)
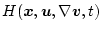 を最小にする
を最小にする
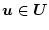 を得る。
を得る。
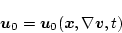 |
(2.312) |
(第3段階)
最適の を求める。
を求める。
![\begin{displaymath}
H_0(\mbox{\boldmath$x$},\nabla \mbox{\boldmath$v$},t)=H[\mbo...
...$},\nabla \mbox{\boldmath$v$},t),\nabla \mbox{\boldmath$v$},t]
\end{displaymath}](img687.png) |
(2.313) |
(第4段階)
ハミルトン・ヤコビの偏微分方程式を解く。
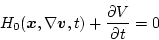 |
(2.314) |
この場合、特定の境界条件で
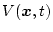 を得る。
を得る。
(第5段階)
最適制御法則を得るために
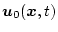 を(第4段階)の結果に代入する。
を(第4段階)の結果に代入する。
 例
例 ![$]$](img114.png)
システム方程式
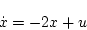 |
(2.315) |
評価関数
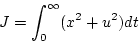 |
(2.316) |
この場合の最適制御法則を求める。
(第1段階)
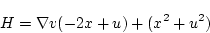 |
(2.317) |
(第2段階)
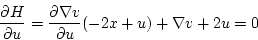 |
(2.318) |
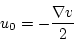 |
(2.319) |
(第3段階)
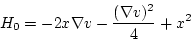 |
(2.320) |
(第4段階)
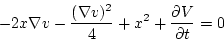 |
(2.321) |
今
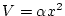 とおき、
とおき、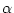 を定数とする。上式は
を定数とする。上式は
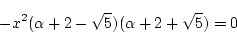 |
(2.322) |
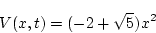 |
(2.323) |
(第5段階)
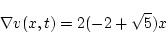 |
(2.324) |
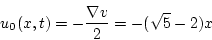 |
(2.325) |
これが求める最適制御法則である。


Next: リカッチの方法 (Riccati equation)
Up: 最適制御法則
Previous: 最適制御法則
Yasunari SHIDAMA
平成15年5月12日
![]() を求める。
を求める。
![]() を得る。
を得る。
![]() を(第4段階)の結果に代入する。
を(第4段階)の結果に代入する。
![]() 例
例 ![]()
![]() とおき、
とおき、![]() を定数とする。上式は
を定数とする。上式は