

Next: 追値制御系の最適制御
Up: 最適制御法則
Previous: ハミルトン・ヤコビの方法 (Hamilton-Jacobi)
(2.298)式の代わりにシステム方程式を
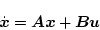 |
(2.326) |
とし、(2.299)式の代わりに評価関数を次の2次形式
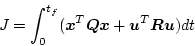 |
(2.327) |
とする。ここで
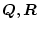 は重み係数といい対称マトリックスで
は重み係数といい対称マトリックスで
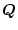 は準正定、
は準正定、
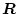 は正定、
は正定、
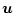 は拘束がないものとする。(2.316)式より
は拘束がないものとする。(2.316)式より
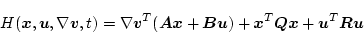 |
(2.328) |
になり、(2.321)式に適用して
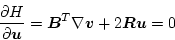 |
(2.329) |
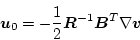 |
(2.330) |
を得る。(2.335)式を(2.333)式に代入すると
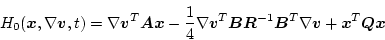 |
(2.331) |
になる。したがってハミルトンヤコビの式は
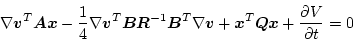 |
(2.332) |
となる。この偏微分方程式を解くのに、次のようにおく。
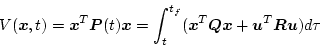 |
(2.333) |
ここに
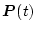 は正定対称行列で
は正定対称行列で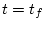 の時、
の時、
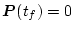 。
上式より
。
上式より
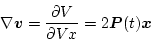 |
(2.334) |
また
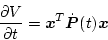 |
(2.335) |
(2.339)式(2.340)式を(2.337)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$x$}^{T}[2\mbox{\boldmath$P$}(t)\mbox{\boldma...
...oldmath$Q$}+\dot{\mbox{\boldmath$P$}}(t)]\mbox{\boldmath$x$}=0
\end{displaymath}](img721.png) |
(2.336) |
になる。また
ゆえ(2.341)式は
![\begin{displaymath}
\mbox{\boldmath$x$}^{T}[\mbox{\boldmath$P$}(t)\mbox{\boldma...
...oldmath$Q$}+\dot{\mbox{\boldmath$P$}}(t)]\mbox{\boldmath$x$}=0
\end{displaymath}](img726.png) |
(2.338) |
となる。任意の
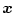 に対し上式が成立するには
に対し上式が成立するには
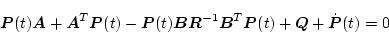 |
(2.339) |
でなければならない。これはリカッチ形の微分方程式である。これを
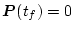 の条件のもとで得られた解
の条件のもとで得られた解
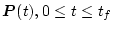 と
(2.339)式を(2.335)式に適用すると
と
(2.339)式を(2.335)式に適用すると
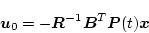 |
(2.340) |
になり
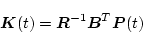 |
(2.341) |
とおくと
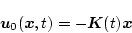 |
(2.342) |
となる。これをブロック図に書くと 図2.19 のごとくなる。
すなわち
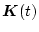 が最適フィードバックゲインを与えることになる。
が最適フィードバックゲインを与えることになる。
図 2.19:
ブロック図
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-8-1.eps} \end{center} \end{figure}](img733.png) |
図 2.20:
変化特性
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-8-2.eps} \end{center} \end{figure}](img734.png) |
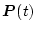 は通常 図2.20 のごとく、初期時刻の間は大体一定値を保ち、
最終時刻に近づいてから変化するという特性を持っている。したがって制御時間が
充分長いときは、
は通常 図2.20 のごとく、初期時刻の間は大体一定値を保ち、
最終時刻に近づいてから変化するという特性を持っている。したがって制御時間が
充分長いときは、
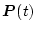 が一定値を保っている間に制御が完了する。したがって
が一定値を保っている間に制御が完了する。したがって
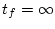 のときは
のときは
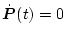 として扱うことができる。
として扱うことができる。
すなわち評価関数が
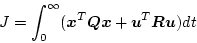 |
(2.343) |
のときは(2.344)式は
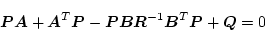 |
(2.344) |
となり、これをリカッチ形代数方程式という。この場合
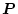 を正定の定数として求め
を正定の定数として求め
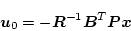 |
(2.345) |
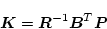 |
(2.346) |
となって、最適フィードバックゲインは定数となる。
いま最適制御法則が得られたとして
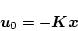 |
(2.347) |
とする。これを評価関数に代入すると
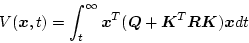 |
(2.348) |
となり、時間で微分すると
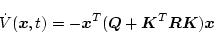 |
(2.349) |
となる。系が安定であるためには、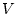 をリアプノフ関数として考えるとき、
をリアプノフ関数として考えるとき、
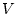 が正定であり、
が正定であり、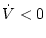 であればよい。そこで
であればよい。そこで
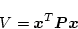 |
(2.350) |
とおく。そのとき
となる。(2.354)式と(2.356)式を等値とすると
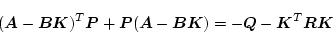 |
(2.352) |
となる。ここで
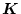 の変化に対して
の変化に対して
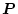 を最小にする。そのため上式を
を最小にする。そのため上式を
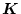 で偏微分して
で偏微分して
 |
(2.353) |
とおくと
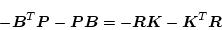 |
(2.354) |
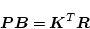 |
(2.355) |
が得られる。これを(2.357)式に代入すると
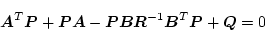 |
(2.356) |
となり、(2.349)式で得られたリカッチ形代数方程式と同じ結果が得られる。
したがって最適フィードバックゲインは(2.351)式より求められる。
 例
例![$]$](img114.png)
システム方程式
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}=\left[
\begin{array}{cc}
0&1\\
...
...th$x$}+\left[
\begin{array}{c}
0\\
1
\end{array} \right]u
\end{displaymath}](img754.png) |
(2.357) |
評価関数
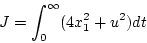 |
(2.358) |
の場合の最適制御方則を求める。
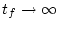 であるから
であるから
![\begin{displaymath}
\mbox{\boldmath$P$}=
\left[
\begin{array}{cc}
P_{11}&P_{12}\\
P_{12}&P_{22}
\end{array} \right]
\end{displaymath}](img757.png) |
(2.359) |
とし、(2.362),(2.363),(2.364)式を(2.349)式に代入すると
![$\displaystyle \left[
\begin{array}{cc}
-P_{12}^{2}+4&P_{11}-P_{12}P_{22}\\
P_{11}-P_{12}P_{22}&2P_{12}-P_{22}^{2}
\end{array}\right]=0$](img761.png) |
|
|
(2.361) |
となり、これより
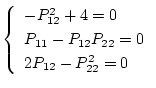 |
|
|
(2.362) |
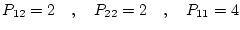 |
|
|
(2.363) |
が得られる。したがって
![$\displaystyle \mbox{\boldmath$P$}=
\left[
\begin{array}{cc}
4&2\\
2&2
\end{array}\right]$](img764.png) |
|
|
(2.364) |
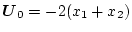 |
|
|
(2.365) |
になる。これをブロック線図にすると 図2.21 となる。
図 2.21:
ブロック線図
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-8-3.eps} \end{center} \end{figure}](img766.png) |
(2.344)式よりベクトル・リカッチ形微分方程式は
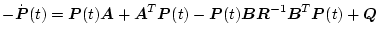 |
|
|
|
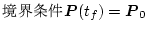 |
|
|
(2.366) |
である。
いま
 なる正方行列を次のようにおく。
なる正方行列を次のようにおく。
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{\mbox{\boldmath$F$}}(t)\\
\dot...
...{\boldmath$F$}(t)\\
\mbox{\boldmath$G$}(t)
\end{array}\right]
\end{displaymath}](img770.png) |
(2.367) |
ただし境界条件
![$\left[
\begin{array}{c}
\mbox{\boldmath$F$}(t_f)\\
\mbox{\boldmath$G$}(t_f)
\e...
...\right]
=
\left[
\begin{array}{c}
I\\
\mbox{\boldmath$P$}_0
\end{array}\right]$](img771.png) とする。
とする。
もし
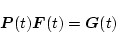 |
(2.368) |
なら、これを偏微分すると
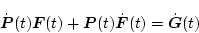 |
(2.369) |
となり、これに(2.372)式の関係を代入すると
となり、元のリカッチ方程式となる。
したがって(2.373)式より
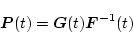 |
(2.370) |
がリカッチ方程式の解である。
そこで(2.372)式の同次方程式の遷移マトリックスを
![\begin{displaymath}
\Phi(t)=
\left[
\begin{array}{cc}
\Phi_{11}(t)&\Phi_{12}(t)\\
\Phi_{21}(t)&\Phi_{22}(t)
\end{array}\right]
\end{displaymath}](img778.png) |
(2.371) |
とすれば、解は境界条件を考慮して
になる。この時、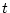 を
を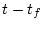 に置き換える。したがって(2.376)式より
に置き換える。したがって(2.376)式より
![\begin{displaymath}
\mbox{\boldmath$P$}(t)=[\Phi_{21}(t,t_f)+\Phi_{22}(t,t_f)\mb...
...
[\Phi_{11}(t,t_f)+\Phi_{12}(t,t_f)\mbox{\boldmath$P$}_0]^{-1}
\end{displaymath}](img783.png) |
(2.373) |
となる。もし
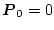 のときは
のときは
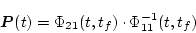 |
(2.374) |
になる。(2.379)又は(2.380)式より解が求められる。
 例
例![$]$](img114.png)
システム方程式
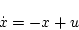 |
(2.375) |
評価関数
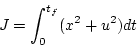 |
(2.376) |
とした場合の最適制御法則を求める。
上式より
となるので、リカッチ微分方程式は
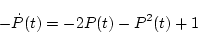 |
(2.377) |
になる。(2.372)式より
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{F}(t)\\
\dot{G}(t)
\end{array}...
...right]
\left[
\begin{array}{c}
F(t)\\
G(t)
\end{array}\right]
\end{displaymath}](img789.png) |
(2.378) |
となるので、この式の遷移マトリックス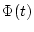 は
は
になる。
境界条件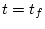 で
で
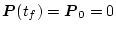 とした場合上式の
とした場合上式の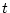 を
を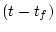 に置き換えて、(2.380)式より
に置き換えて、(2.380)式より
となる。
ゆえに(2.345)式より
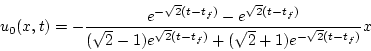 |
(2.381) |
となる。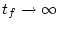 とした場合
とした場合
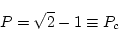 |
(2.382) |
という定数になる。したがって
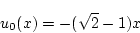 |
(2.383) |
となる。これをブロック線図にしたのが 図2.22 である。
図 2.22:
ブロック線図
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-8-4.eps} \end{center} \end{figure}](img808.png) |
システム方程式が次のようにプロパー(厳密プロパーでなく)な場合を考える。
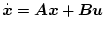 |
|
|
(2.384) |
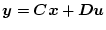 |
|
|
(2.385) |
評価関数を
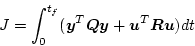 |
(2.386) |
とする。
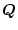 は準正定対称、
は準正定対称、
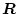 は正定対称行列とする。上式に(2.391)
式を適用すると
は正定対称行列とする。上式に(2.391)
式を適用すると
![\begin{displaymath}
J=\int_0^{t_f}[\mbox{\boldmath$x$}^T\mbox{\boldmath$C$}^T \m...
...^T\mbox{\boldmath$Q$}\mbox{\boldmath$C$}\mbox{\boldmath$x$}]dt
\end{displaymath}](img812.png) |
(2.387) |
となる。ここで
とおくと、(2.393)式は
![\begin{displaymath}
J=\int_0^{t_f}[\mbox{\boldmath$x$}^T\bar{\mbox{\boldmath$Q$}...
...oldmath$u$}^T\bar{\mbox{\boldmath$S$}}^T\mbox{\boldmath$x$}]dt
\end{displaymath}](img816.png) |
(2.391) |
になる。(2.326)式より
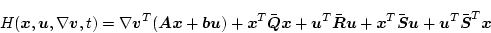 |
(2.392) |
となり、(2.311)式に適用して、
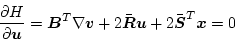 |
(2.393) |
より
![\begin{displaymath}
\mbox{\boldmath$u$}_0=-\frac{1}{2}\bar{\mbox{\boldmath$R$}}^...
...\boldmath$v$}+2\bar{\mbox{\boldmath$S$}}^T\mbox{\boldmath$x$}]
\end{displaymath}](img819.png) |
(2.394) |
を得る。(2.400)式を(2.398)式に代入すると、
となる。 の場合ハミルトン・ヤコビの式は
の場合ハミルトン・ヤコビの式は
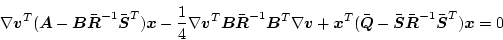 |
(2.396) |
になる。ここで(2.389)式と同様
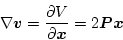 |
(2.397) |
とおくと、
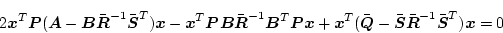 |
(2.398) |
となり、左辺の第1項を(2.342)式と同様の方法で分けると
| |
|
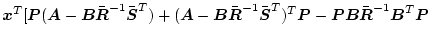 |
|
| |
|
![$\displaystyle \hspace{2cm} {}+(\bar{\mbox{\boldmath$Q$}}-\bar{\mbox{\boldmath$S...
...ar{\mbox{\boldmath$R$}}^{-1}\bar{\mbox{\boldmath$S$}}^T)]\mbox{\boldmath$x$}
=0$](img827.png) |
(2.399) |
になり、任意の
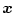 に対し上式が成立するには
に対し上式が成立するには
| |
|
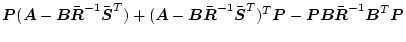 |
|
| |
|
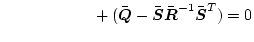 |
(2.400) |
が満たされればよい。これがリッカチ型の代数方程式である。
この式の解
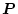 を用い、(2.400)式より
を用い、(2.400)式より
![\begin{displaymath}
\mbox{\boldmath$u$}_0=-\frac{1}{2}\bar{\mbox{\boldmath$R$}}^...
...{\boldmath$P$}+\bar{\mbox{\boldmath$S$}}^T]\mbox{\boldmath$x$}
\end{displaymath}](img830.png) |
(2.401) |
が得られ最適フィード・バックゲインは
![\begin{displaymath}
\mbox{\boldmath$K$}=\bar{\mbox{\boldmath$R$}}^{-1}[\mbox{\boldmath$B$}^T\mbox{\boldmath$P$}+\bar{\mbox{\boldmath$S$}}^T]
\end{displaymath}](img831.png) |
(2.402) |
となる。
このことは
とし、評価関数を
![\begin{displaymath}
\int_0^{\infty}[\mbox{\boldmath$x$}(t)^T(\bar{\mbox{\boldmat...
...}(t)^T\bar{\mbox{\boldmath$R$}}\bar{\mbox{\boldmath$u$}}(t)]dt
\end{displaymath}](img833.png) |
(2.403) |
とした場合のレギュレータ問題と等しい。ただし
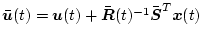 である。なお(2.409)式は次のように表示することもできる。
である。なお(2.409)式は次のように表示することもできる。
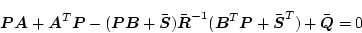 |
(2.404) |
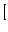 例
例![$]$](img114.png)
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}=\left[
\begin{array}{cc}
0&0\\
1&...
...\begin{array}{c}
1\\
1
\end{array}\right] \mbox{\boldmath$u$}
\end{displaymath}](img836.png) |
(2.405) |
![\begin{displaymath}
\mbox{\boldmath$y$}=\left[
\begin{array}{cc}
1&0\\
0&1
\end...
...
\begin{array}{c}
1\\
0
\end{array}\right]\mbox{\boldmath$u$}
\end{displaymath}](img837.png) |
(2.406) |
かつ
の場合、(2.394)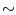 (2.396)式より
(2.396)式より
を得る。したがって
となり、これらを(2.406)式に代入すると
になる。ゆえに
の関係を得る。
(2.416)式より
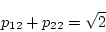 |
(2.410) |
これを(2.415)式に代入すると
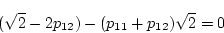 |
(2.411) |
(2.417),(2.418)式を用いて、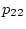 及び
及び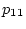 を
を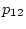 で表し、これを(2.414)式に代入し、整理すると
で表し、これを(2.414)式に代入し、整理すると
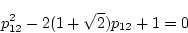 |
(2.412) |
になり、これを解いて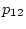 を求め、(2.417),(2.418)式より
を求め、(2.417),(2.418)式より
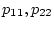 を求め、
を求め、
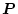 が正定であるようにすると
が正定であるようにすると
![\begin{displaymath}
\mbox{\boldmath$P$}=
\left[
\begin{array}{cc}
0.472&0.222\\
0.22&1.194
\end{array}\right]
\end{displaymath}](img857.png) |
(2.413) |
を得る。したがって(2.408)式より
がフィードバックゲインとなる。


Next: 追値制御系の最適制御
Up: 最適制御法則
Previous: ハミルトン・ヤコビの方法 (Hamilton-Jacobi)
Yasunari SHIDAMA
平成15年5月12日
![]() は通常 図2.20 のごとく、初期時刻の間は大体一定値を保ち、
最終時刻に近づいてから変化するという特性を持っている。したがって制御時間が
充分長いときは、
は通常 図2.20 のごとく、初期時刻の間は大体一定値を保ち、
最終時刻に近づいてから変化するという特性を持っている。したがって制御時間が
充分長いときは、
![]() が一定値を保っている間に制御が完了する。したがって
が一定値を保っている間に制御が完了する。したがって
![]() のときは
のときは
![]() として扱うことができる。
として扱うことができる。
![]() 例
例![]()
![]() であるから
であるから
![]() なる正方行列を次のようにおく。
なる正方行列を次のようにおく。
![$\left[
\begin{array}{c}
\mbox{\boldmath$F$}(t_f)\\
\mbox{\boldmath$G$}(t_f)
\e...
...\right]
=
\left[
\begin{array}{c}
I\\
\mbox{\boldmath$P$}_0
\end{array}\right]$](img771.png) とする。
とする。
![]() 例
例![]()
![]() で
で
![]() とした場合上式の
とした場合上式の![]() を
を![]() に置き換えて、(2.380)式より
に置き換えて、(2.380)式より
![\begin{displaymath}
\mbox{\boldmath$Q$}=\left[\begin{array}{cc}
1&0\\
0&1
\end{array} \right] \quad , \quad
\mbox{\boldmath$R$}=1
\end{displaymath}](img838.png)
![\begin{displaymath}\bar{\mbox{\boldmath$Q$}}=
\left[
\begin{array}{cc}
1&0\\
0&...
...ldmath$S$}}=
\left[
\begin{array}{c}
1\\
0
\end{array}\right]
\end{displaymath}](img840.png)
![\begin{displaymath}
\mbox{\boldmath$A$}-\mbox{\boldmath$B$}\bar{\mbox{\boldmath$...
...^T=
\left[
\begin{array}{cc}
-0.5&0\\
0.5&0
\end{array}\right]\end{displaymath}](img841.png)
![\begin{displaymath}
\bar{\mbox{\boldmath$Q$}}-\bar{\mbox{\boldmath$S$}}\bar{\mbo...
...$}}^T=
\left[
\begin{array}{cc}
0.5&0\\
0&1
\end{array}\right]\end{displaymath}](img842.png)