


Next: モデル追随問題
Up: 追値制御系の最適制御
Previous: 評価関数
目標値
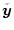 が次の状態方程式で表されるものとする。
ただし初期値は
が次の状態方程式で表されるものとする。
ただし初期値は
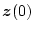 である。
である。
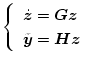 |
|
|
(2.439) |
またシステム方程式は(2.422)式、評価関数は(2.445)式であるとする。
いま状態
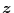 はすべて可観測であるとし、システムの状態変数
はすべて可観測であるとし、システムの状態変数
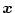 と
目標値の状態変数
と
目標値の状態変数
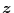 を含めた新しい状態変数を
を含めた新しい状態変数を
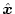 とする。
そのとき
とする。
そのとき
![\begin{displaymath}
\hat{\mbox{\boldmath$x$}}=\left[
\begin{array}{c}
\mbox{\boldmath$x$}\\
\mbox{\boldmath$z$}
\end{array}
\right]
\end{displaymath}](img910.png) |
(2.440) |
で表され、新しいマトリックスとして
を用いる。このようにした場合新しい状態方程式は
となり評価関数は
を(2.445)式に代入して
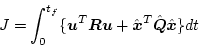 |
(2.443) |
を得る。(2.449)式のシステム方程式、(2.451)式の評価関数は
レギュレータ問題と同じ形であり
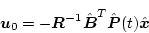 |
(2.444) |
と置けば
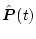 は次のリカッチ方程式の解として求められる。
は次のリカッチ方程式の解として求められる。
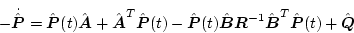 |
(2.445) |
ただし
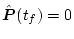
![\begin{displaymath}
\hat{P}(t)=
\left[
\begin{array}{cc}
\mbox{\boldmath$P$}&\mb...
...oldmath$P$}_{21}&\mbox{\boldmath$P$}_{22}
\end{array}
\right]
\end{displaymath}](img926.png) |
(2.446) |
と置けば(2.453)式は分解して
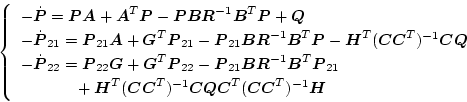 |
(2.447) |
となり、各式を解いて
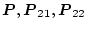 を求めることができる。
(2.452)式に(2.464)式を代入すれば
を求めることができる。
(2.452)式に(2.464)式を代入すれば
が得られ、
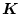 がフィードバックゲイン、
がフィードバックゲイン、
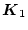 が
フィードフォワードゲインとなる。
が
フィードフォワードゲインとなる。
このことは図2.23(a)で示すシステムを(b)で示すように目標値発生系を
等価システムの中に含めたものとして、レギュレータ問題として取り扱ったことを
意味している。
図 2.23:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-9-1.eps} \end{center} \end{figure}](img933.png) |
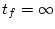 のときは(2.453)式の左辺を
のときは(2.453)式の左辺を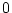 として
として
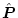 を求める。
このときは
を求める。
このときは
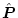 は定数となる。
は定数となる。
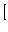 例
例![$]$](img114.png)
システム方程式
![\begin{displaymath}
\left\{
\begin{array}{l}
\dot{\mbox{\boldmath$x$}}=
\left[
\...
...
\end{array}
\right]
\mbox{\boldmath$x$}
\end{array}\right .
\end{displaymath}](img935.png) |
(2.449) |
目標発生源方程式
![\begin{displaymath}
\left\{
\begin{array}{cc}
\dot{\mbox{\boldmath$z$}}=
\left[
...
...
\end{array}
\right]
\mbox{\boldmath$z$}
\end{array}\right .
\end{displaymath}](img936.png) |
(2.450) |
評価関数
![\begin{displaymath}
J==\int_{0}^{\infty}[4(y-\tilde{y})^2+\mbox{\boldmath$u$}^{2}]dt
\end{displaymath}](img937.png) |
(2.451) |
の場合の最適追値制御系を求める。
この場合
であり、
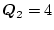 であるから
であるから
になる。
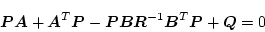 |
(2.452) |
の解は(2.369)式より
である。いま
とすると
となるので
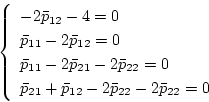 |
(2.454) |
より
![\begin{displaymath}
\mbox{\boldmath$P$}_{21}=
\left[
\begin{array}{cc}
-4&-2\\
-1.2&-0.8
\end{array}
\right]
\end{displaymath}](img949.png) |
(2.455) |
が得られる。ゆえに(2.456)式より
![\begin{displaymath}
\left.\begin{array}{c}
\mbox{\boldmath$K$}=\mbox{\boldmath$R...
...egin{array}{cc}
2&0.8
\end{array}
\right]
\end{array}\right\}
\end{displaymath}](img950.png) |
(2.456) |
となる。
図2.24はこのようにして構成した制御系の目標値に対する追随状況を示している。
図 2.24:
![\begin{figure}\begin{center}
\psbox[scale=0.90]{eps/2-9-2.eps} \end{center} \end{figure}](img951.png) |



Next: モデル追随問題
Up: 追値制御系の最適制御
Previous: 評価関数
Yasunari SHIDAMA
平成15年5月12日
![]() が次の状態方程式で表されるものとする。
ただし初期値は
が次の状態方程式で表されるものとする。
ただし初期値は
![]() である。
である。
![]() はすべて可観測であるとし、システムの状態変数
はすべて可観測であるとし、システムの状態変数
![]() と
目標値の状態変数
と
目標値の状態変数
![]() を含めた新しい状態変数を
を含めた新しい状態変数を
![]() とする。
そのとき
とする。
そのとき
![]() のときは(2.453)式の左辺を
のときは(2.453)式の左辺を![]() として
として
![]() を求める。
このときは
を求める。
このときは
![]() は定数となる。
は定数となる。
![]() 例
例![]()
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$A$}=
\left[
\begin{array}...
...c}
1&0
\end{array}
\right]
&
\mbox{\boldmath$R$}=1
\end{array}\end{displaymath}](img938.png)
![\begin{displaymath}\mbox{\boldmath$Q$}=\mbox{\boldmath$C$}^T\mbox{\boldmath$Q$}_...
...$C$}=
\left[
\begin{array}{cc}
4&0\\
0&0
\end{array}
\right]
\end{displaymath}](img940.png)
![\begin{displaymath}\mbox{\boldmath$P$}=
\left[
\begin{array}{cc}
4&2\\
2&2
\end{array}
\right]
\end{displaymath}](img942.png)
![\begin{displaymath}\mbox{\boldmath$P$}_{21}=
\left[
\begin{array}{cc}
\bar{p}_{11}&\bar{p}_{12}\\
\bar{p}_{21}&\bar{p}_{22}
\end{array}
\right]
\end{displaymath}](img943.png)