


Next: モデル・マッチング
Up: 追値制御系の最適制御
Previous: モデル追随問題
前項のモデル追値問題の場合は目標値の性質が予め判っていなければならないうえ、
完全にモデルに追随させるというのは困難である。
ここに述べるパーフェクト・モデル・フォローイング方式は任意の入力に対して
完全にモデルに追随させることができる。
いまプラントの状態方程式を
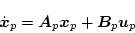 |
(2.460) |
モデルの状態方程式を
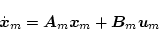 |
(2.461) |
とする。但しプラントとモデルは同次数とする。そして制御系を図2.26のごとく構成する。
図 2.26:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-9-4.eps} \end{center} \end{figure}](img964.png) |
したがって
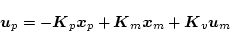 |
(2.462) |
の関係がある。
(2.468),(2.469),(2.470)式より
となる。ここで
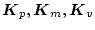 の間に
の間に
| |
|
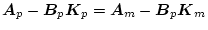 |
(2.463) |
| |
|
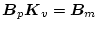 |
(2.464) |
の関係をもたせると
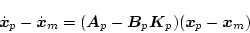 |
(2.465) |
となる。この式は
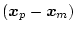 に関する同次方程式であるので
に関する同次方程式であるので
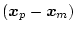 の初期値が
の初期値が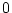 のときは、
制御期間中は
のときは、
制御期間中は
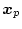 は常に
は常に
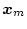 に等しい。すなわちモデルに完全に追随する。
に等しい。すなわちモデルに完全に追随する。
また、もし
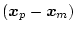 の初期値が
の初期値が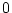 でない場合でも、
でない場合でも、
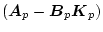 が安定な根を与えるように設計してあれば漸近的に
が安定な根を与えるように設計してあれば漸近的に
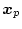 は
は
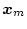 と一致し、完全に追随するようになる。
と一致し、完全に追随するようになる。
したがって、設計に際し、まず
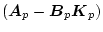 が安定になるように
が安定になるように
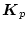 を設定する。とくに
を設定する。とくに
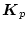 をプラントの最適フィードバックゲインに
なるように設定することが望ましい。
をプラントの最適フィードバックゲインに
なるように設定することが望ましい。
次に(2.472)式と(2.473)式より
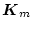 、
、
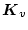 を決定する。
但し、(2.472)式を書き直すと、
を決定する。
但し、(2.472)式を書き直すと、
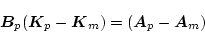 |
(2.466) |
になり、この式において
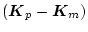 の解が得られるためには
の解が得られるためには
![\begin{displaymath}
rank\mbox{\boldmath$B$}_{p}=rank[\mbox{\boldmath$B$}_{p},(\mbox{\boldmath$A$}_{p}-\mbox{\boldmath$A$}_{m})]
\end{displaymath}](img982.png) |
(2.467) |
でなければならない。また(2.473)式で
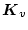 の解が得られるためには
の解が得られるためには
![\begin{displaymath}
rank\mbox{\boldmath$B$}_{p}=rank[\mbox{\boldmath$B$}_{p},\mbox{\boldmath$B$}_{m}]
\end{displaymath}](img983.png) |
(2.468) |
でなければならない。したがって任意のモデルに対して常にパーフェクト・
モデル・フォローイングが可能であるということではない。
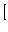 例
例![$]$](img114.png)
プラントの状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}_{p}=
\left[
\begin{array}{cc}
0&1\...
...in{array}{c}
0\\
1
\end{array}\right]
\mbox{\boldmath$u$}_{p}
\end{displaymath}](img984.png) |
(2.469) |
モデルの状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}_{m}=
\left[
\begin{array}{cc}
0&1\...
...in{array}{c}
0\\
1
\end{array}\right]
\mbox{\boldmath$u$}_{m}
\end{displaymath}](img985.png) |
(2.470) |
とする。
今
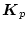 を求める際に、評価関数を
を求める際に、評価関数を
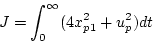 |
(2.471) |
にとると、前の例題で求めたごとく
![\begin{displaymath}
\mbox{\boldmath$K$}_{p}=
\left[
\begin{array}{cc}
2&2
\end{array}\right]
\end{displaymath}](img987.png) |
(2.472) |
になる。このとき
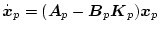 の根は
の根は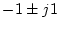 となり安定である。
となり安定である。
![\begin{displaymath}
\mbox{\boldmath$A$}_{p}-\mbox{\boldmath$A$}_{m}=
\left[
\beg...
...ight]
=
\left[
\begin{array}{cc}
0&0\\
0&2
\end{array}\right]
\end{displaymath}](img990.png) |
(2.473) |
となるので
![\begin{displaymath}
\left\{
\begin{array}{l}
rank[\mbox{\boldmath$B$}_{p},(\mbox...
...egin{array}{c}
0\\
1
\end{array}\right]
=1
\end{array}\right.
\end{displaymath}](img991.png) |
(2.474) |
ゆえ、
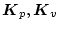 の解は存在する。すなわち
の解は存在する。すなわち
より
![\begin{displaymath}
\mbox{\boldmath$K$}_{m}=
\left[
\begin{array}{cc}
2&0\\
\end{array}\right]
\end{displaymath}](img996.png) |
(2.476) |
また
![\begin{displaymath}
\mbox{\boldmath$B$}_{p}\mbox{\boldmath$K$}_{v}=
\left[
\begin{array}{c}
0\\
1
\end{array}\right]
\end{displaymath}](img997.png) |
(2.477) |
より
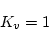 |
(2.478) |
が得られる。
いまモデル出力
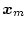 を入力
を入力
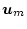 に対する伝達関数で表示すると
に対する伝達関数で表示すると
![\begin{displaymath}
\mbox{\boldmath$x$}_{m}(s)=
\left[
\begin{array}{cc}
s&-1 ...
...
1\\
s
\end{array}\right]}{s^2+2s}
\mbox{\boldmath$u$}_{m}(s)
\end{displaymath}](img1001.png) |
(2.479) |
となる。一方プラントの出力
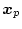 をモデル入力
をモデル入力
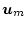 からの伝達関数で
表示すると
からの伝達関数で
表示すると
となって、モデルの伝達関数と全く等しくなる。したがって
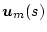 が如何なる形であっても
が如何なる形であっても
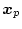 と
と
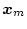 は完全追随することがわかる。
は完全追随することがわかる。



Next: モデル・マッチング
Up: 追値制御系の最適制御
Previous: モデル追随問題
Yasunari SHIDAMA
平成15年5月12日
![]() の初期値が
の初期値が![]() でない場合でも、
でない場合でも、
![]() が安定な根を与えるように設計してあれば漸近的に
が安定な根を与えるように設計してあれば漸近的に
![]() は
は
![]() と一致し、完全に追随するようになる。
と一致し、完全に追随するようになる。
![]() が安定になるように
が安定になるように
![]() を設定する。とくに
を設定する。とくに
![]() をプラントの最適フィードバックゲインに
なるように設定することが望ましい。
をプラントの最適フィードバックゲインに
なるように設定することが望ましい。
![]() 、
、
![]() を決定する。
但し、(2.472)式を書き直すと、
を決定する。
但し、(2.472)式を書き直すと、
![]() を求める際に、評価関数を
を求める際に、評価関数を
![]() を入力
を入力
![]() に対する伝達関数で表示すると
に対する伝達関数で表示すると