


Next: 状態観測器 (State Observer)
Up: 追値制御系の最適制御
Previous: モデル・マッチング
前項のパーフェクト・モデル・フォローイング方式では、プラントとモデルが同次数であり、
かつ両者の零点が等しくなければならず、その上(2.476)、(2.477)式で示した
rankの条件を満たさねばならないという厳しい制限のため追随できるモデルの特性が限定される。
ここで述べる拡張形の場合は以下に示すように
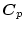 、
、
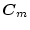 を用い、
プラントの出力
を用い、
プラントの出力
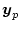 をモデルの出力
をモデルの出力
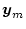 に完全に一致させるもので
フィード・フォワードゲイン
に完全に一致させるもので
フィード・フォワードゲイン
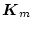 も伝達関数要素を含めた
も伝達関数要素を含めた
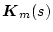 としているので
次数や零点の制限が緩和され広範囲のモデルに追随できる方式である。
としているので
次数や零点の制限が緩和され広範囲のモデルに追随できる方式である。
プラントとモデルのシステム方程式を次とする。
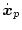 |
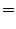 |
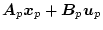 |
(2.489) |
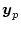 |
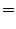 |
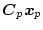 |
(2.490) |
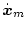 |
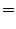 |
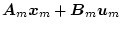 |
(2.491) |
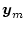 |
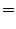 |
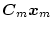 |
(2.492) |
ただし
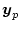 と
と
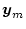 は同次数とする。
は同次数とする。
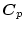 、
、
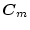 は
は
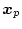 、
、
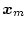 の中の
追随を必要とする変数を指定するためのものである。
の中の
追随を必要とする変数を指定するためのものである。
図 2.28:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-9-6.eps} \end{center} \end{figure}](img1037.png) |
システムの構成は図2.28のごとくであり
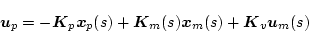 |
(2.493) |
の関係がある。入力
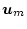 に対し、
に対し、
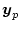 が
が
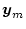 と完全に一致するためには、
と完全に一致するためには、
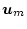 から
から
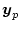 までの伝達関数と
までの伝達関数と
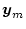 までの伝達関数を等しくする必要がある。すなわち
までの伝達関数を等しくする必要がある。すなわち
| |
|
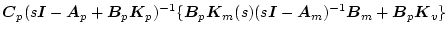 |
|
| |
|
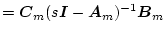 |
(2.494) |
となるようにする。そのために
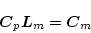 |
(2.495) |
となるような定数行列
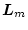 を導入する。この
を導入する。この
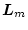 は
は
![\begin{displaymath}
rank\mbox{\boldmath$C$}_p=rank[\mbox{\boldmath$C$}_p\quad ,\quad \mbox{\boldmath$C$}_m]
\end{displaymath}](img1043.png) |
(2.496) |
が満足されれば存在する。次にこの
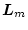 を用いて
を用いて
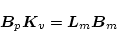 |
(2.497) |
とおく。このとき
![\begin{displaymath}
rank\mbox{\boldmath$B$}_p=rank[\mbox{\boldmath$B$}_p\quad ,\quad \mbox{\boldmath$L$}_m\mbox{\boldmath$B$}_m]
\end{displaymath}](img1045.png) |
(2.498) |
が満足するように
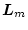 が選定できれば、
が選定できれば、
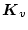 は存在する。この(2.507)式の関係を(2.504)式に代入し、変形すると次式となる。
は存在する。この(2.507)式の関係を(2.504)式に代入し、変形すると次式となる。
したがって
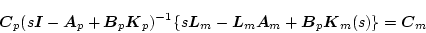 |
(2.500) |
の関係があれば(2.509)式が成立する。ここでさらに
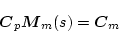 |
(2.501) |
という
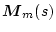 なる行列を導入する。この
なる行列を導入する。この
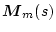 は一般的には
は一般的には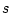 の関数であって
の関数であって
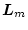 とは異なるが、定数にとった場合
とは異なるが、定数にとった場合
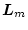 と等しい場合もある。この
と等しい場合もある。この
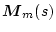 も(2.506)式が満足されれば存在する。(2.510)、(2.511)式より
も(2.506)式が満足されれば存在する。(2.510)、(2.511)式より
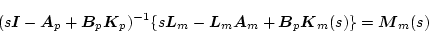 |
(2.502) |
という関係が得られ、これを書き直すと
となり、右辺を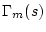 とおく。このとき
とおく。このとき
![\begin{displaymath}
rank\mbox{\boldmath$B$}_p=rank[\mbox{\boldmath$B$}_p\quad ,\quad \mbox{\boldmath$\Gamma$}_m(s)]
\end{displaymath}](img1057.png) |
(2.504) |
が成立するように
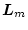 、
、
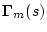 が選定できれば(2.513)式から
が選定できれば(2.513)式から
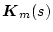 が、(2.507)式から
が、(2.507)式から
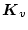 が求められる。
が求められる。
[例]
プラントのシステム方程式を
モデルのシステム方程式を
とする。プラントが3次、モデルが2次かつ単入力ゆえ、
![\begin{displaymath}
\mbox{\boldmath$L$}_m=\left[\begin{array}{cc}
l_{11} & l_{12}\\
l_{21} & l_{22}\\
l_{31} & l_{32}
\end{array}\right]
\end{displaymath}](img1065.png) |
(2.509) |
とおく。(2.505)式より
![\begin{displaymath}
\mbox{\boldmath$C$}_p\mbox{\boldmath$L$}_m= \left[\begin{arr...
...dmath$C$}_m=
\left[\begin{array}{cc}
1&0
\end{array}\right]
\end{displaymath}](img1066.png) |
(2.510) |
ゆえに
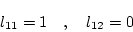 |
(2.511) |
したがって
![\begin{displaymath}
\mbox{\boldmath$L$}_m\mbox{\boldmath$B$}_m= \left[\begin{arr...
...gin{array}{c}
0\\
16l_{22}\\
16l_{32}
\end{array}\right]
\end{displaymath}](img1068.png) |
(2.512) |
(2.508)式より
| |
![$\textstyle rank[\mbox{\boldmath$B$}_p\quad , \quad \mbox{\boldmath$L$}_m\mbox{\...
...\\
0 & 16l_{22} \\
5 & 16l_{32}
\end{array}\right]=
rank\mbox{\boldmath$B$}_p$](img1069.png) |
|
|
| |
![$\textstyle =
rank\left[\begin{array}{c}
0 \\
0 \\
5
\end{array}\right]=1$](img1070.png) |
|
(2.513) |
ゆえに(2.523)式が成立するためには
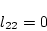 |
(2.514) |
一方
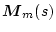 も(2.511)式より、(2.520)式の場合と同様
も(2.511)式より、(2.520)式の場合と同様
![\begin{displaymath}
\mbox{\boldmath$M$}_m(s)=\left[\begin{array}{cc}
1 & 0 \\
...
...s) & m_{22}(s) \\
m_{31}(s) & m_{32}(s)
\end{array}\right]
\end{displaymath}](img1072.png) |
(2.515) |
という形になる。単入力ゆえ
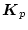 を次のようにおく。
を次のようにおく。
![\begin{displaymath}
\mbox{\boldmath$K$}_p=[k_{p1}\quad , \quad k_{p2}\quad , \quad k_{p3}]
\end{displaymath}](img1074.png) |
(2.516) |
以上を(2.513)式の右辺に代入すると
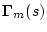 は次式となる。
は次式となる。
(2.514)式を満足するためには
![$rank[\mbox{\boldmath$B$}_p\quad ,\quad\mbox{\boldmath$\Gamma$}_m(s)]$](img1078.png) でなければならないから、上記の上2桁は全部0とする必要がある。故に1列目側の
でなければならないから、上記の上2桁は全部0とする必要がある。故に1列目側の
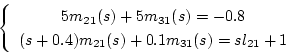 |
(2.517) |
より
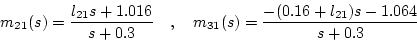 |
(2.518) |
2列目側の
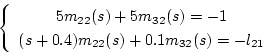 |
(2.519) |
より
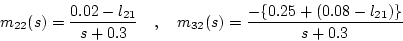 |
(2.520) |
これを
 の3行目に代入すると、1列目の方は
の3行目に代入すると、1列目の方は
2列目の方は
両方とも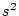 の項を0とするように
の項を0とするように
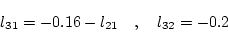 |
(2.522) |
にとる。また
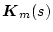 が簡単な形になるように3行2列目を定数とするため
(2.533)式の右辺第2項と第3項の比を
が簡単な形になるように3行2列目を定数とするため
(2.533)式の右辺第2項と第3項の比を 対
対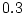 にとる。すなわち
にとる。すなわち
| |
|
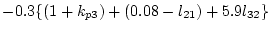 |
|
| |
|
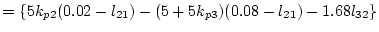 |
(2.523) |
これより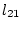 を算出すると
を算出すると
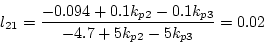 |
(2.524) |
を得る。したがって(2.534)式より
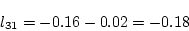 |
(2.525) |
になる。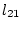 を(2.529)、(2.531)式に代入すると
を(2.529)、(2.531)式に代入すると
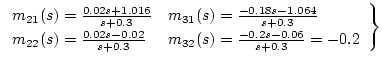 |
|
|
(2.526) |
が得られるので、これらを
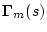 の3行目に代入すると
の3行目に代入すると
になる。いま
![$\mbox{\boldmath$K$}_p=[k_{p1} , k_{p2} , k_{p3}]=[-0.8 , 0.1 , 1.2]$](img1109.png) にとると
にとると
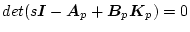 の根は、
の根は、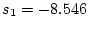 と
と
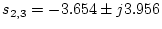 の安定な系となる。この値は
の安定な系となる。この値は
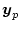 と
と
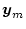 に初期値誤差があった場合、それの減衰状況の指標となるので、なるべく速やかに減衰するように
に初期値誤差があった場合、それの減衰状況の指標となるので、なるべく速やかに減衰するように
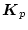 の値を定める必要がある。上記
の値を定める必要がある。上記
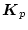 の値を(2.539)(2.540)式に代入すると
の値を(2.539)(2.540)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$\Gamma$}_m(s)=\left[\begin{array}{cc}
0&0\\...
...\
\frac{-(3.78s+11.436)}{(s+0.3)} & -1.26
\end{array}\right]
\end{displaymath}](img1113.png) |
(2.529) |
になる。一方
![$\mbox{\boldmath$K$}_m(s)=[k_{m1}(s) , k_{m2}(s)]$](img1114.png) とすると
とすると
![\begin{displaymath}
\mbox{\boldmath$B$}_p\mbox{\boldmath$K$}_m(s)=\left[\begin{a...
...{cc}
0&0\\
0&0\\
5k_{m1}(s)&5k_{m2}(s)
\end{array}\right]
\end{displaymath}](img1115.png) |
(2.530) |
になるので(2.513)式より
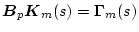 にすると
にすると
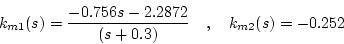 |
(2.531) |
が得られる。また前記
 を(2.507)式に適用して
を(2.507)式に適用して
![\begin{displaymath}
\mbox{\boldmath$L$}_m\mbox{\boldmath$B$}_m=\left[\begin{arra...
...=\left[\begin{array}{c}
0 \\
0 \\
5
\end{array}\right]K_v
\end{displaymath}](img1119.png) |
(2.532) |
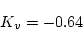 |
(2.533) |
が得られ、以上のようにして
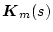 、
、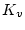 が決定される。
が決定される。
これらを用いると完全追随になることを以下に示す。プラントの閉ループ伝達関数は
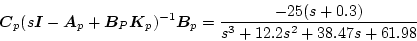 |
(2.534) |
であり、モデルの伝達関数は
![\begin{displaymath}
(s\mbox{\boldmath$I$}-\mbox{\boldmath$A$}_m)^{-1}\mbox{\bold...
...\begin{array}{c}
16 \\
16s
\end{array}\right]}{s^2+5.6s+16}
\end{displaymath}](img1123.png) |
(2.535) |
である。モデルとフィード・フォワード・ゲインを加えた部分の伝達関数は
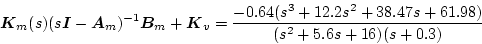 |
(2.536) |
したがって、モデル入力からプラント出力までの伝達関数は
| |
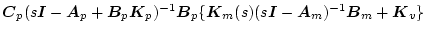 |
|
|
| |
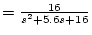 |
|
(2.537) |
になってモデルのそれと等しく、完全追随になっている。



Next: 状態観測器 (State Observer)
Up: 追値制御系の最適制御
Previous: モデル・マッチング
Yasunari SHIDAMA
平成15年5月12日
![]() 、
、
![]() を用い、
プラントの出力
を用い、
プラントの出力
![]() をモデルの出力
をモデルの出力
![]() に完全に一致させるもので
フィード・フォワードゲイン
に完全に一致させるもので
フィード・フォワードゲイン
![]() も伝達関数要素を含めた
も伝達関数要素を含めた
![]() としているので
次数や零点の制限が緩和され広範囲のモデルに追随できる方式である。
としているので
次数や零点の制限が緩和され広範囲のモデルに追随できる方式である。