


Next: 同形観測器
Up: 状態観測器 (State Observer)
Previous: 状態観測器 (State Observer)
このプラントを図2.29中の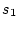 とする。この状態変数のうち直接観測可能
な出力
とする。この状態変数のうち直接観測可能
な出力
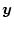 と入力
と入力
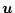 を他のシステム
を他のシステム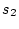 に加え、その出力を
に加え、その出力を
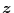 とする。
とする。
図 2.29:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-1.eps} \end{center} \end{figure}](img1135.png) |
いま、この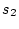 システムの状態方程式を次式とする。
システムの状態方程式を次式とする。
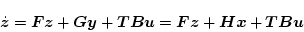 |
(2.540) |
但し
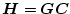
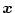 の次数が
の次数が
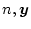 の次数が
の次数が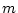 であれば、
であれば、
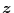 の次数は
の次数は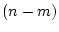 である。
また
である。
また
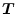 はある変換行列を意味する。この
はある変換行列を意味する。この
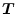 を(2.550)式に掛け、(2.552)式より引くと
を(2.550)式に掛け、(2.552)式より引くと
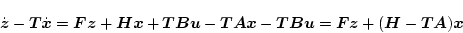 |
(2.541) |
となる。もし
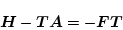 |
(2.542) |
という関係があると、(2.553)式は
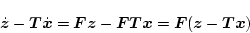 |
(2.543) |
になる。この式の解は
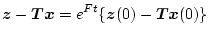 |
|
|
(2.544) |
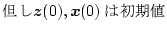 |
|
|
|
である。この式は
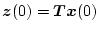 であれば
であれば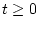 において
において
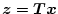 であり、またもし
であり、またもし
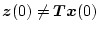 でも
でも
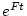 が減衰すれば
が減衰すれば
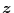 は漸近的に
は漸近的に
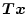 に一致することを意味しており、
この
に一致することを意味しており、
この
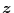 を用いて
を用いて
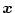 を推定することができる。
を推定することができる。
観測器の設計法としては、先ず安定でかつ早く収束するように、
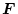 を定める。
つぎに
を定める。
つぎに
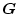 (叉は
(叉は
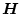 )の一部を与えて
)の一部を与えて
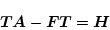 |
(2.545) |
より
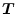 を求める。
を求める。
![$
\left[
\begin{array}{c}
\mbox{\boldmath$T$}\\
\mbox{\boldmath$C$}
\end{array}\right]
$](img1155.png) は
は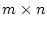 の行列であり、逆行列が可能であれば
の行列であり、逆行列が可能であれば
![$
\left[
\begin{array}{c}
\mbox{\boldmath$z$}\\
\mbox{\boldmath$y$}
\end{array}...
...ox{\boldmath$T$}\\
\mbox{\boldmath$C$}
\end{array}\right]
\mbox{\boldmath$x$}
$](img1156.png) ゆえ
ゆえ
![\begin{displaymath}
\hat{\mbox{\boldmath$x$}}=
\left[
\begin{array}{c}
\mbox{\bo...
...
\mbox{\boldmath$z$}\\
\mbox{\boldmath$y$}
\end{array}\right]
\end{displaymath}](img1157.png) |
(2.546) |
より推定値
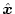 が求められる。(2.552)式と(2.558)式によって
観測器が構成される。
が求められる。(2.552)式と(2.558)式によって
観測器が構成される。
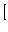 例
例![$]$](img114.png)
図 2.30:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-2.eps} \end{center} \end{figure}](img1158.png) |
図2.30に示すプラントに置いて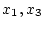 および
および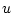 が測定可能で、
が測定可能で、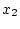 および
および
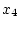 を測定する観測器を設計する。
同図のプラントの状態方程式は
を測定する観測器を設計する。
同図のプラントの状態方程式は
である。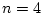 、
、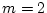 ゆえ
ゆえ
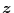 の次数は
の次数は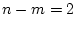 であるから(2.552)式
が安定で、かつ早く収束するように
であるから(2.552)式
が安定で、かつ早く収束するように
![\begin{displaymath}
\begin{array}{cc}
\mbox{\boldmath$F$}=
\left[
\begin{array}{...
...}
g_{11}&g_{12}\\
g_{21}&g_{22}
\end{array}\right]
\end{array}\end{displaymath}](img1167.png) |
(2.549) |
とおくと、
![\begin{displaymath}
\mbox{\boldmath$H$}=\mbox{\boldmath$G$}\mbox{\boldmath$C$}=
...
...ccc}
g_{11}&0&g_{12}&0\\
g_{21}&0&g_{22}&0
\end{array}\right]
\end{displaymath}](img1168.png) |
(2.550) |
になる。
![\begin{displaymath}
\mbox{\boldmath$T$}=
\left[
\begin{array}{cccc}
t_{11}&t_{12}&t_{13}&t_{14}\\
t_{21}&t_{22}&t_{23}&t_{24}
\end{array}\right]
\end{displaymath}](img1169.png) |
(2.551) |
とすると(2.557)式は
になる。この式は
| |
![$\textstyle \left[
\begin{array}{cccc}
(t_{11}-t_{14})&(t_{11}+t_{12})&(t_{12}+2...
...1}-t_{24})&(t_{21}+t_{22})&(t_{22}+2t_{23})&(t_{23}+3t_{24})
\end{array}\right]$](img1173.png) |
|
|
| |
![$\textstyle =
\left[
\begin{array}{cccc}
g_{11}&0&g_{12}&0\\
g_{21}&0&g_{22}&0
\end{array}\right]$](img1174.png) |
|
(2.553) |
となり、
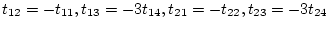 および
および
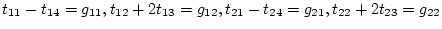 の関係が得られ、これより次のようになる。
の関係が得られ、これより次のようになる。
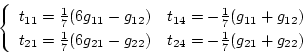 |
(2.554) |
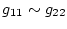 の値は任意にとれるが、なるべく簡単になるように
の値は任意にとれるが、なるべく簡単になるように
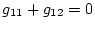 、
、
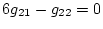 および、
および、
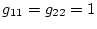 とすると
とすると
![\begin{displaymath}
\mbox{\boldmath$T$}
=
\left[
\begin{array}{cccc}
1&-1&0&0\\
0&0&\frac{1}{2}&-\frac{1}{6}
\end{array}\right]
\end{displaymath}](img1182.png) |
(2.555) |
になる。この
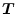 および
および
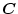 を用いると(2.558)式より
を用いると(2.558)式より
![\begin{displaymath}
\hat{\mbox{\boldmath$x$}}=
\left[
\begin{array}{cccc}
1&-1&0...
...[
\begin{array}{c}
z_1\\
z_2\\
x_1\\
x_3
\end{array}\right]
\end{displaymath}](img1183.png) |
(2.556) |
が得られる。この式より
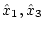 はそのまま
はそのまま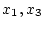 が用いられ、
が用いられ、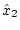 および
および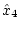 は
は
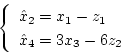 |
(2.557) |
より得られる。
であるから上記
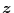 は(2.562)式より
は(2.562)式より
![\begin{displaymath}
\dot{\mbox{\boldmath$z$}}=
\left[\begin{array}{cc}
-3&0\\
...
...\left[\begin{array}{c}
0\\
-\frac{1}{6}
\end{array}\right]u
\end{displaymath}](img1192.png) |
(2.560) |
の関係から得られる。(2.569)式、(2.572)式より観測器のブロック図は図2.31のごとくなる。
図 2.31:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-3.eps} \end{center} \end{figure}](img1193.png) |



Next: 同形観測器
Up: 状態観測器 (State Observer)
Previous: 状態観測器 (State Observer)
Yasunari SHIDAMA
平成15年5月12日
![]() とする。この状態変数のうち直接観測可能
な出力
とする。この状態変数のうち直接観測可能
な出力
![]() と入力
と入力
![]() を他のシステム
を他のシステム![]() に加え、その出力を
に加え、その出力を
![]() とする。
とする。
![]() システムの状態方程式を次式とする。
システムの状態方程式を次式とする。
![]() を定める。
つぎに
を定める。
つぎに
![]() (叉は
(叉は
![]() )の一部を与えて
)の一部を与えて
![$
\left[
\begin{array}{c}
\mbox{\boldmath$T$}\\
\mbox{\boldmath$C$}
\end{array}\right]
$](img1155.png) は
は![$
\left[
\begin{array}{c}
\mbox{\boldmath$z$}\\
\mbox{\boldmath$y$}
\end{array}...
...ox{\boldmath$T$}\\
\mbox{\boldmath$C$}
\end{array}\right]
\mbox{\boldmath$x$}
$](img1156.png) ゆえ
ゆえ