Next: 低次元観測器
Up: 状態観測器 (State Observer)
Previous: 基礎理論 (Luenbergerの方法)
前項の方法において、
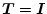 とした場合である。このとき(2.554)式より
とした場合である。このとき(2.554)式より
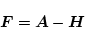 |
(2.561) |
になるので、(2.552)式は
となる。上式より(2.560)式を引くと
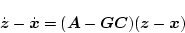 |
(2.563) |
になる。したがって、もし
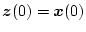 なら
なら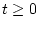 の間
の間
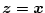 であり、
であり、
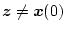 でも、もし
でも、もし
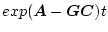 が減衰を
するなら、
が減衰を
するなら、
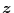 は
は
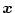 に漸近的に一致する。そしてこのとき
に漸近的に一致する。そしてこのとき
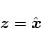 |
(2.564) |
となる。但しこの場合は
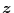 の次元は
の次元は
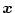 の次元と等しくなる。
の次元と等しくなる。
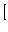 例1
例1![$]$](img114.png)
プラントの状態方程式が
で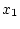 が観測され
が観測され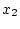 を推定する場合を考える。
を推定する場合を考える。
![\begin{displaymath}
\mbox{\boldmath$G$}=\left[\begin{array}{c}
g_1\\
g_2
\end...
...}{cc}
g_1&0\\
g_2&0
\end{array}\right]=
\mbox{\boldmath$H$}
\end{displaymath}](img1208.png) |
(2.567) |
とおく。
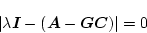 |
(2.568) |
の根が安定で、かつ早く減衰をするように指定する。
すなわち
に対し、
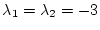 と指定すると
と指定すると
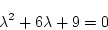 |
(2.570) |
になるので、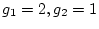 が得られる。すなわち
が得られる。すなわち
となるので、観測器は(2.574)式より
![\begin{displaymath}
\dot{\mbox{\boldmath$z$}}=
\left[
\begin{array}{cc}
-4&1\\
...
...right]
y
+
\left[
\begin{array}{c}
0\\
1
\end{array}\right]
u
\end{displaymath}](img1217.png) |
(2.571) |
になり、
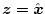 となる。
となる。
この観測器をブロック図で示すと図2.32のごとくなる。
図 2.32:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-4.eps} \end{center} \end{figure}](img1219.png) |
図 2.33:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-5.eps} \end{center} \end{figure}](img1220.png) |
同形観測器の場合は、前項で述べたパーフェクト・モデル・フォローイングの
手法を用いて設計することもできる。すなわち図2.33のごとくモデルの部分をプラントとし、
プラントの部分を観測器とすれば観測器の出力はプラントの出力に完全に追随するので、
状態推定が出来る。このとき、(2.472)式と(2.473)式の関係は
となる。ここに
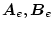 は観測器のシステムおよび駆動マトリックスである。
は観測器のシステムおよび駆動マトリックスである。
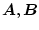 が与えられており、
が与えられており、
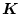 は測定不可能な状態変数に対応する要素を
は測定不可能な状態変数に対応する要素を
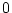 とする。
とする。
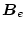 は測定可能な状態変数の次数と、入力
は測定可能な状態変数の次数と、入力
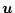 の次数とを加えた
次数を持ち、かつ(2.585)式から
の次数とを加えた
次数を持ち、かつ(2.585)式から
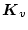 が求められるように設定する。そして
が求められるように設定する。そして
![$[\mbox{\boldmath$A$}_e-\mbox{\boldmath$B$}_e\mbox{\boldmath$K$}_e]$](img1228.png) は観測器の根が安定になるように指定をし、
(2.584)式より
は観測器の根が安定になるように指定をし、
(2.584)式より
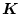 の未定の部分を決定する。その時観測器の状態方程式は
の未定の部分を決定する。その時観測器の状態方程式は
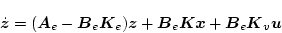 |
(2.574) |
となる。
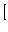 例2
例2![$]$](img114.png)
前例の場合に適用する。
であるので
とおく。そのとき(2.585)式より
になる。また(2.584)式より
となる。
![$det\vert\lambda \mbox{\boldmath$I$}-[\mbox{\boldmath$A$}_e-\mbox{\boldmath$B$}_e\mbox{\boldmath$K$}_e]\vert=0$](img1234.png) の根
の根
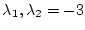 と
なるように
と
なるように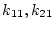 を設定する。
を設定する。
より、
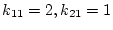 となる。以上より観測器の方程式(2.586)式は
となる。以上より観測器の方程式(2.586)式は
![\begin{displaymath}
\dot{\mbox{\boldmath$z$}}=
\left[
\begin{array}{cc}
-4&1\\
...
...\begin{array}{c}
0\\
1
\end{array}\right]
\mbox{\boldmath$u$}
\end{displaymath}](img1239.png) |
(2.575) |
になる。これは(2.583)式と同じ結果であることを示している。



Next: 低次元観測器
Up: 状態観測器 (State Observer)
Previous: 基礎理論 (Luenbergerの方法)
Yasunari SHIDAMA
平成15年5月12日
![]() とした場合である。このとき(2.554)式より
とした場合である。このとき(2.554)式より
![]() 例1
例1![]()
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$G$}=
\left[
\begin{array}...
...
\begin{array}{cc}
-4&1\\
-1&-2
\end{array}\right]
\end{array}\end{displaymath}](img1216.png)
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$A$}=
\left[
\begin{array}...
...$}=
\left[
\begin{array}{cc}
1&0
\end{array}\right]
\end{array}\end{displaymath}](img1230.png)
![\begin{displaymath}
\begin{array}{cc}
\mbox{\boldmath$B$}_e=
\left[
\begin{array...
...{array}{cc}
k_{11}&0\\
k_{21}&0
\end{array}\right]
\end{array}\end{displaymath}](img1231.png)
![\begin{displaymath}\mbox{\boldmath$K$}_{v}=\mbox{\boldmath$B$}_e^{-1}\mbox{\boldmath$B$}=
\left[
\begin{array}{c}
0\\
1
\end{array}\right]
\end{displaymath}](img1232.png)
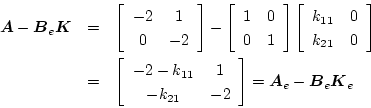
![]() の根
の根
![]() と
なるように
と
なるように![]() を設定する。
を設定する。