


Next: カルマン・フィルタ型観測器
Up: 状態観測器 (State Observer)
Previous: 同形観測器
同形観測器の場合、全状態変数を推定するが測定可能な状態変数まで推定しているので
次数が多くなり無駄がある。そこで必要な状態変数だけ推定しようとするのが低次元観測器である。
いま、
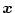 のうち測定可能な変数を
のうち測定可能な変数を
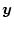 、測定不能、すなわち推定したい変数を
、測定不能、すなわち推定したい変数を
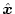 としたとき
としたとき
![$\bar{\mbox{\boldmath$x$}}=
\left[
\begin{array}{c}
\mbox{\boldmath$y$}\\
\hat{\mbox{\boldmath$x$}}
\end{array}\right]
$](img1240.png) とする。
とする。
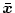 は
は
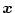 と同じ変数で構成されているが、順序が
異っている。(2.550)式を
と同じ変数で構成されているが、順序が
異っている。(2.550)式を
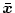 に書き換えた場合
に書き換えた場合
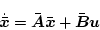 |
(2.576) |
になる。この式はさらに
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{\mbox{\boldmath$y$}}\\
\dot{\h...
...
\mbox{\boldmath$B$}_2
\end{array}\right]
\mbox{\boldmath$u$}
\end{displaymath}](img1243.png) |
(2.577) |
と書き、これを分離すると
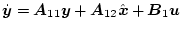 |
|
|
(2.578) |
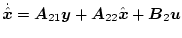 |
|
|
(2.579) |
となる。
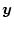 の次元は
の次元は
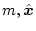 の次元は
の次元は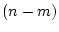 である。いま、
である。いま、
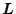 という
という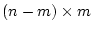 のマトリックスを導入し、(2.590)式に
のマトリックスを導入し、(2.590)式に
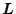 を前から掛けて、
(2.591)式から引くと
を前から掛けて、
(2.591)式から引くと
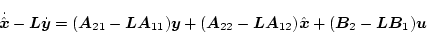 |
(2.580) |
になる。ここで
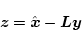 |
(2.581) |
とすると、(2.593)式は
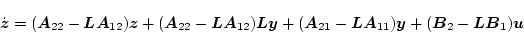 |
(2.582) |
となる。
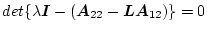 が安定な固有値を持つように
が安定な固有値を持つように
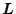 を設定する。(2.594)式は
を設定する。(2.594)式は
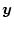 と
と
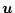 より
より
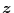 が
求められる式であり、この
が
求められる式であり、この
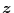 と
と
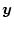 を(2.593)式に適用すれば
を(2.593)式に適用すれば
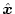 が求められる。
が求められる。
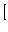 例
例![$]$](img114.png)
前例の場合に適用する。(2.577),(2.578)式より
であるから、これを(2.590)式、(2.591)式に適用すると
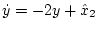 |
|
|
(2.583) |
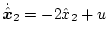 |
|
|
(2.584) |
となる。すなわち
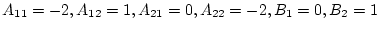 である。ゆえに
である。ゆえに
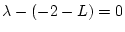 の根が安定となるように、すなわち
の根が安定となるように、すなわち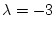 にとると、
にとると、
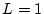 となる。これを(2.594)式に適用すると
となる。これを(2.594)式に適用すると
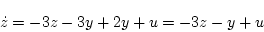 |
(2.585) |
となる。(2.593)式より
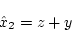 |
(2.586) |
となる。(2.597)式、(2.598)式より観測器が構成され、これを示したのが
図2.34(a)である。(2.597)式に(2.598)式を代入すると
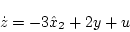 |
(2.587) |
となる。この式によって構成した観測器が同図(b)である。
図 2.34:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-6.eps} \end{center} \end{figure}](img1262.png) |



Next: カルマン・フィルタ型観測器
Up: 状態観測器 (State Observer)
Previous: 同形観測器
Yasunari SHIDAMA
平成15年5月12日
![$\bar{\mbox{\boldmath$x$}}=
\left[
\begin{array}{c}
\mbox{\boldmath$y$}\\
\hat{\mbox{\boldmath$x$}}
\end{array}\right]
$](img1240.png) とする。
とする。
![]() のうち測定可能な変数を
のうち測定可能な変数を
![]() 、測定不能、すなわち推定したい変数を
、測定不能、すなわち推定したい変数を
![]() としたとき
としたとき
![$\bar{\mbox{\boldmath$x$}}=
\left[
\begin{array}{c}
\mbox{\boldmath$y$}\\
\hat{\mbox{\boldmath$x$}}
\end{array}\right]
$](img1240.png) とする。
とする。
![]() は
は
![]() と同じ変数で構成されているが、順序が
異っている。(2.550)式を
と同じ変数で構成されているが、順序が
異っている。(2.550)式を
![]() に書き換えた場合
に書き換えた場合
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$A$}=
\left[
\begin{array}...
...$}=
\left[
\begin{array}{cc}
1&0
\end{array}\right]
\end{array}\end{displaymath}](img1230.png)