


Next: ロバスト制御 (Robust Control)
Up: 状態観測器 (State Observer)
Previous: 低次元観測器
入力信号に統計的性質を持つ雑音が加わり、かつ出力信号に同様の観測雑音が含まれているような場合にはカルマン・フィルタ型観測器が用いられる。この場合のシステムは次式で表現される。
ここで
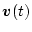 は入力に加わる雑音、
は入力に加わる雑音、
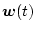 は観測時に加わる雑音で、それぞれ白色雑音である。したがって自己相関および両者間の相互相関がなく、一定のパワースペクトルを持ち、次のような性質で表現される。
は観測時に加わる雑音で、それぞれ白色雑音である。したがって自己相関および両者間の相互相関がなく、一定のパワースペクトルを持ち、次のような性質で表現される。
![$\displaystyle E[\mbox{\boldmath$v$}(t)]=E[\mbox{\boldmath$w$}(t)]=0$](img1268.png) |
|
|
(2.590) |
![$\displaystyle E[\mbox{\boldmath$v$}(t),\mbox{\boldmath$w$}^T(t)]=0$](img1269.png) |
|
|
(2.591) |
![$\displaystyle E[\mbox{\boldmath$v$}(t),\mbox{\boldmath$v$}^T(\tau)]=\mbox{\boldmath$Q$}\delta(t-\tau)$](img1270.png) |
|
|
(2.592) |
![$\displaystyle E[\mbox{\boldmath$w$}(t),\mbox{\boldmath$w$}^T(\tau)]=\mbox{\boldmath$R$}\delta(t-\tau)$](img1271.png) |
|
|
(2.593) |
ここに
![$E[\mbox{\boldmath$v$}(t)]$](img1272.png) は確率変数
は確率変数
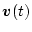 の期待値を、また
の期待値を、また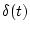 は
は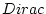 のデルタ関数を表す。
のデルタ関数を表す。
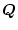 、
、
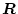 はそれぞれ対称な準正定および正定行列である。
はそれぞれ対称な準正定および正定行列である。
時間区間の間に上記システムから得られた観測データから
時刻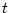 における状態
における状態
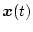 の推定値
の推定値
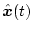 を求めるには次の評価関数を最小にするようにする。
を求めるには次の評価関数を最小にするようにする。
この場合、レギュレータ問題の場合と同様の手法を用いて最適フィルタ・ゲイン
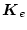 を求める。すなわち次のリカッチ型微分方程式
を求める。すなわち次のリカッチ型微分方程式
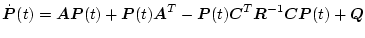 |
|
|
(2.594) |
ただし
の正定対称な解
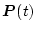 (これを推定誤差共分散という)より
(これを推定誤差共分散という)より
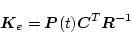 |
(2.595) |
が得られる。最適推定値
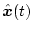 はこの
はこの
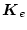 を用いて次式で与えられる。
を用いて次式で与えられる。
![$\displaystyle \dot{\hat{\mbox{\boldmath$x$}}}=\mbox{\boldmath$A$}\hat{\mbox{\bo...
...$K$}_e
[\mbox{\boldmath$y$}(t)-\mbox{\boldmath$C$}\hat{\mbox{\boldmath$x$}}(t)]$](img1282.png) |
|
|
(2.596) |
![$\displaystyle ただし\hat{\mbox{\boldmath$x$}}(0)=E[\mbox{\boldmath$x$}(0)]$](img1283.png) |
|
|
|
したがって、観測器は(2.608)式に基づき、図2.35のブロック図のような形で実現される。
図 2.35:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-10-7.eps} \end{center} \end{figure}](img1284.png) |
 例
例![$]$](img114.png) 次のシステムのカルマン・フィルタ型観測器を設計する。ただし
次のシステムのカルマン・フィルタ型観測器を設計する。ただし
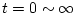 の区間とする。
の区間とする。
このとき
であり、また
より
になる。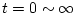 ゆえ(2.606)式は
ゆえ(2.606)式は
とした場合
になり、
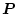 の正定解は
の正定解は
![\begin{displaymath}
\mbox{\boldmath$P$}=\left[\begin{array}{cc}
2 & 4 \\
4 & 4
\end{array}\right]
\end{displaymath}](img1298.png) |
(2.600) |
となる。したがってフィルタ・ゲイン
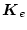 は(2.607)式より
は(2.607)式より
![\begin{displaymath}
\mbox{\boldmath$K$}_e=-\mbox{\boldmath$PC$}^TR^{-1}=-\left[\...
...right]1=
\left[\begin{array}{c}
-2 \\
-4
\end{array}\right]
\end{displaymath}](img1299.png) |
(2.601) |
のように得られる。したがって観測器はプラントの
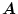 、
、
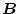 、
、
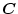 および
および
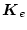 を用いて
を用いて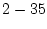 図のように構成される。
図のように構成される。



Next: ロバスト制御 (Robust Control)
Up: 状態観測器 (State Observer)
Previous: 低次元観測器
Yasunari SHIDAMA
平成15年5月12日
![]() は入力に加わる雑音、
は入力に加わる雑音、
![]() は観測時に加わる雑音で、それぞれ白色雑音である。したがって自己相関および両者間の相互相関がなく、一定のパワースペクトルを持ち、次のような性質で表現される。
は観測時に加わる雑音で、それぞれ白色雑音である。したがって自己相関および両者間の相互相関がなく、一定のパワースペクトルを持ち、次のような性質で表現される。
![]() における状態
における状態
![]() の推定値
の推定値
![]() を求めるには次の評価関数を最小にするようにする。
を求めるには次の評価関数を最小にするようにする。
![]() を求める。すなわち次のリカッチ型微分方程式
を求める。すなわち次のリカッチ型微分方程式
![]() 例
例![]() 次のシステムのカルマン・フィルタ型観測器を設計する。ただし
次のシステムのカルマン・フィルタ型観測器を設計する。ただし
![]() の区間とする。
の区間とする。
![\begin{displaymath}
\mbox{\boldmath$A$}=\left[\begin{array}{cc}
-1 & 1 \\
0 &...
...ath$C$}=\left[\begin{array}{cc}
1 & 0 \\
\end{array}\right]
\end{displaymath}](img1290.png)
![\begin{eqnarray*}
&&E\left[\begin{array}{cc}
\left[\begin{array}{c}
0 \\
v(t...
...\boldmath$Q$}\delta(t-\tau)\\
&&E[w(t),w(\tau)]=R\delta(t-\tau)
\end{eqnarray*}](img1291.png)
![\begin{displaymath}
\mbox{\boldmath$Q$}=\left[\begin{array}{cc}
0 & 0 \\
0 & 16
\end{array}\right],\qquad
R=1
\end{displaymath}](img1292.png)
![\begin{displaymath}
\mbox{\boldmath$P$}=\left[\begin{array}{cc}
p_{11} & p_{12} \\
p_{12} & p_{22}
\end{array}\right]
\end{displaymath}](img1293.png)