


Next: 特異値による感度解析
Up: ロバスト制御 (Robust Control)
Previous: ロバスト制御とは
ある与えられたプラント
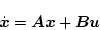 |
(2.602) |
のパラメータ 、
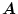 ,
,
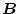 が変動をすると、その特性が変化する。このパラメータ変動に対する
特性の変化を感度(Sensitivity)という。一般に制御系においては特性の変化のないことが望ましい
から感度が小さい方が良い。
が変動をすると、その特性が変化する。このパラメータ変動に対する
特性の変化を感度(Sensitivity)という。一般に制御系においては特性の変化のないことが望ましい
から感度が小さい方が良い。
二つのシステムの感度を比較するに際して、パラメータが変動する前、すなわち基準値
(これをノミナル値という)において、二つのシステムが等しい特性を有している必要
がある。(これをノミナル値等価という)パラメータ変動後両システムに同一の入力
を加えたとき出力の基準状態に対する変動分の大きさによって感度を比較するとき軌道
感度という。
いまノミナル値等価な開ループ系と閉ループ系の感度を比較してみる。そのため前者には
添字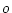 を後者には
を後者には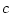 を付すことにし、ノミナル値において同一入力を加えたときの
出力を
を付すことにし、ノミナル値において同一入力を加えたときの
出力を
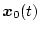 ,
,
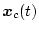 とする。このとき
とする。このとき
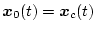 である。
パラメータ変動後、同じ入力を加えた場合の出力を
である。
パラメータ変動後、同じ入力を加えた場合の出力を
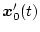 ,
,
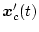 としたとき、変動分はそれぞれ
としたとき、変動分はそれぞれ
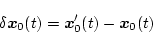 |
(2.603) |
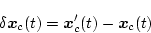 |
(2.604) |
で表せる。両システムの軌道感度基準は、総ての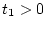 に対して
に対して
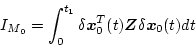 |
(2.605) |
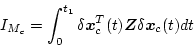 |
(2.606) |
で定義される。ここで
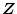 は対称正定または準正定な重み行列である。
は対称正定または準正定な重み行列である。
もし
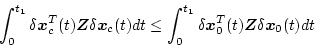 |
(2.607) |
であれば閉ループ系が開ループ系より感度が減少していることを意味している。
(2.619)式に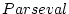 の定理を適用すると
の定理を適用すると
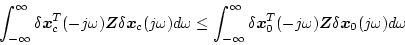 |
(2.608) |
となり、周波数領域で示した軌道感度比較を示している。
図 2.36:
開ループ系と閉ループ系
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-1.eps} \end{center} \end{figure}](img1318.png) |
いま図2.36に示すノミナル値等価な開ループ系と閉ループ系を考える。ノミナル値
等価であるので
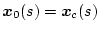 ,
,
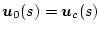 である。パラメータ変動による出力変動は開ループ系の場合、
である。パラメータ変動による出力変動は開ループ系の場合、
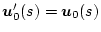 であるので、
であるので、
であり、閉ループ系の場合は
にな、るので、
となり、
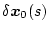 と
と
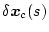 との関係は
との関係は
になる。
![\begin{displaymath}
\mbox{\boldmath$S$}(s) = [\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(s)\mbox{\boldmath$F$}(s)]^{-1}
\end{displaymath}](img1337.png) |
(2.613) |
としたとき、これを比較感度行列といい、その逆行列
![\begin{displaymath}
\mbox{\boldmath$T$}(s) = [\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(s)\mbox{\boldmath$F$}(s)]
\end{displaymath}](img1338.png) |
(2.614) |
を還送差(Return Difference)という。
ここで、パラメータ変動が小さく、かつ
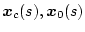 および
および
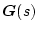 がパラメータに連続的に依存するとした場合、(2.625)、(2.626)式
は近似的に
がパラメータに連続的に依存するとした場合、(2.625)、(2.626)式
は近似的に
とおくことができる。これは次の理由による。
いま
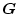 の中で変動するパラメータのパラメータ・ベクトルを
の中で変動するパラメータのパラメータ・ベクトルを
![\begin{displaymath}
\mbox{\boldmath$\alpha$} = [\alpha_1,\alpha_2,\cdots,\alpha_k]^T
\end{displaymath}](img1344.png) |
(2.617) |
とする。
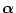 をノミナルの時の値としたとき、(2.614)式
のプラントの状態方程式を
をノミナルの時の値としたとき、(2.614)式
のプラントの状態方程式を
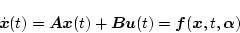 |
(2.618) |
とし、パラメータが
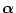 から
から
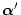 に変化したとき
に変化したとき
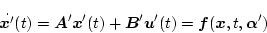 |
(2.619) |
とする。この式を
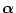 の点に関してテーラー展開をすると
の点に関してテーラー展開をすると
になる。パラメータ変化分
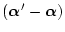 が小さいとき上式は次のように近似される。
が小さいとき上式は次のように近似される。
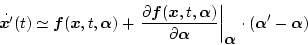 |
(2.621) |
したがって(2.633)式から(2.630)式を引くと
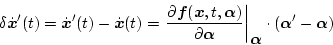 |
(2.622) |
となる。上式を初期値を0として積分すると
になる。
開ループ系に対し、この式をs領域で表示すると
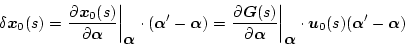 |
(2.624) |
となり、閉ループ系に対しては
となる。
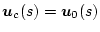 であり、かつ
であり、かつ
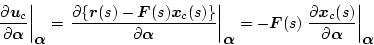 |
(2.626) |
であるから
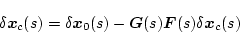 |
(2.627) |
すなわち
![\begin{displaymath}
\delta\mbox{\boldmath$x$}_0(s) = [\mbox{\boldmath$I$}+\mbox{...
...th$G$}(s)\mbox{\boldmath$F$}(s)]\delta\mbox{\boldmath$x$}_c(s)
\end{displaymath}](img1364.png) |
(2.628) |
になり、(2.627)式、(2.628)式と置いても良いことが云える。
(2.640)式を、(2.620)式に代入すると
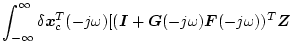 |
|
|
|
![$\displaystyle \times (\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\omega)\mbox{\bo...
...a))-\mbox{\boldmath$Z$}]\delta\mbox{\boldmath$x$}_c(j\omega)\cdot d\omega \ge 0$](img1366.png) |
|
|
(2.629) |
になり、この式が成立するための十分条件は
![\begin{displaymath}[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(-j\omega)\mbox{\bold...
...(j\omega)\mbox{\boldmath$F$}(j\omega)] \ge \mbox{\boldmath$Z$}
\end{displaymath}](img1367.png) |
(2.630) |
である。この式が成立するときは閉ループ系が開ループ系より感度が減少する。
閉ループ系の場合、フィードバックゲイン
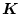 を次の評価関数を最小とする最適
フィードバックにとるものとする。
を次の評価関数を最小とする最適
フィードバックにとるものとする。
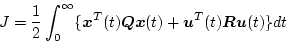 |
(2.631) |
この時
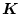 は次のリカッチ形方程式
は次のリカッチ形方程式
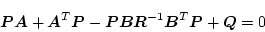 |
(2.632) |
の解
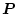 より
より
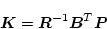 |
(2.633) |
として求められる。(2.644)式に
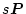 を加え、かつ引き、
(2.645)式を適用すると
を加え、かつ引き、
(2.645)式を適用すると
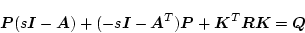 |
(2.634) |
となる。この式に左から
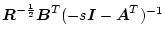 を、
右から
を、
右から
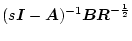 を掛け両辺に
を掛け両辺に
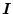 を加えると
を加えると
となる。上式の左辺は、(2.645)式を代入すると
になるので、これを(2.647)式に代入し、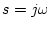 とすると
とすると
となる。
一方(2.642)式において,
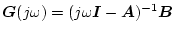 、
、
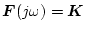 とし、かつ
とし、かつ
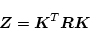 |
(2.635) |
とおいたとき
![$\displaystyle [\mbox{\boldmath$I$}+(-j\omega\mbox{\boldmath$I$}-\mbox{\boldmath...
...I$}+(j\omega\mbox{\boldmath$I$}-\mbox{\boldmath$A$})^{-1}
\mbox{\boldmath$BK$}]$](img1389.png) |
|
|
|
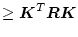 |
|
|
(2.636) |
になる。これは書き直すと
![$\mbox{\boldmath$K$}^T\mbox{\boldmath$R$}^{\frac{1}{2}}[\mbox{\boldmath$I$}+\mbo...
...x{\boldmath$A$}^T)^{-1}
\mbox{\boldmath$K$}^T\mbox{\boldmath$R$}^{\frac{1}{2}}]$](img1391.png)
![$\times [\mbox{\boldmath$I$}+\mbox{\boldmath$R$}^{\frac{1}{2}}\mbox{\boldmath$K$...
...1}\mbox{\boldmath$BR$}^{-\frac{1}{2}}]
V{R}^{\frac{1}{2}}\mbox{\boldmath$K$}$](img1392.png)
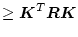
より
![\begin{displaymath}[\mbox{\boldmath$I$}+\mbox{\boldmath$R$}^{\frac{1}{2}}\mbox{\...
...1}\mbox{\boldmath$BR$}^{-\frac{1}{2}}]
\ge \mbox{\boldmath$I$}
\end{displaymath}](img1394.png) |
(2.637) |
となる。(2.652)式の左辺とノミナル値のときの(2.649)式の
左辺は等しいので
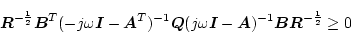 |
(2.638) |
になる。この式は恒等的に成立する。したがって、閉ループのフィードバックを最適
制御にとった場合、(2.650)式の重みのもとで閉ループ系の感度は開ループ系の感度より減少する。
(2.653)式において
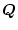 を大きくとる程その不等性が大きくなり、
すなわちより感度を減少することができる。
を大きくとる程その不等性が大きくなり、
すなわちより感度を減少することができる。



Next: 特異値による感度解析
Up: ロバスト制御 (Robust Control)
Previous: ロバスト制御とは
Yasunari SHIDAMA
平成15年5月12日
![]() を後者には
を後者には![]() を付すことにし、ノミナル値において同一入力を加えたときの
出力を
を付すことにし、ノミナル値において同一入力を加えたときの
出力を
![]() ,
,
![]() とする。このとき
とする。このとき
![]() である。
パラメータ変動後、同じ入力を加えた場合の出力を
である。
パラメータ変動後、同じ入力を加えた場合の出力を
![]() ,
,
![]() としたとき、変動分はそれぞれ
としたとき、変動分はそれぞれ
![]() ,
,
![]() である。パラメータ変動による出力変動は開ループ系の場合、
である。パラメータ変動による出力変動は開ループ系の場合、
![]() であるので、
であるので、
![]() および
および
![]() がパラメータに連続的に依存するとした場合、(2.625)、(2.626)式
は近似的に
がパラメータに連続的に依存するとした場合、(2.625)、(2.626)式
は近似的に
![]() の中で変動するパラメータのパラメータ・ベクトルを
の中で変動するパラメータのパラメータ・ベクトルを
![]() を次の評価関数を最小とする最適
フィードバックにとるものとする。
を次の評価関数を最小とする最適
フィードバックにとるものとする。
![]() 、
、
![]() とし、かつ
とし、かつ
![]() を大きくとる程その不等性が大きくなり、
すなわちより感度を減少することができる。
を大きくとる程その不等性が大きくなり、
すなわちより感度を減少することができる。