


Next: 特異値による安定性の解析
Up: ロバスト制御 (Robust Control)
Previous: システム感度(Sensitivity)
行列
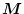 の転置行列を
の転置行列を
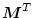 、共役行列を
、共役行列を
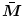 としたとき、
としたとき、
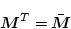 |
(2.639) |
である行列をエルミット行列という。
また
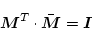 |
(2.640) |
であるとき、
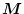 をユニタリー行列という。
をユニタリー行列という。
次に別に任意の行列
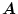 に対し、その共役転値行列を
に対し、その共役転値行列を
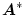 としたとき、
としたとき、
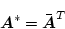 |
(2.641) |
であり、これより
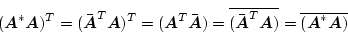 |
(2.642) |
となるから
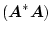 はエルミット行列である。
はエルミット行列である。
エルミット行列は準正定行列であるから、その固有値は正の実数または0である。
すなわち、
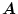 が
が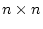 の行列で、
の行列で、
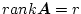 のとき、
のとき、
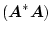 の固有値を
の固有値を
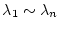 とすると、
とすると、
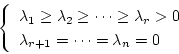 |
(2.643) |
である。
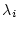 は正の実数ゆえ
は正の実数ゆえ
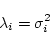 |
(2.644) |
とおける。そのとき
![\begin{displaymath}
\mbox{\boldmath$\Sigma$} = \left[
\begin{array}{c\vert c}
\...
...ght]
ただし
\Sigma_1 = diag[\sigma_1,\sigma_2,\cdots,\sigma_r]
\end{displaymath}](img1409.png) |
(2.645) |
としたとき、
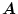 を
を
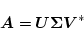 |
(2.646) |
で表すことを特異値分解といい、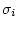 を特異値という。
を特異値という。
ここで
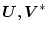 はそれぞれ
はそれぞれ
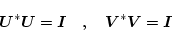 |
(2.647) |
のユニタリー行列である。(2.661)式より
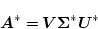 |
(2.648) |
ゆえ
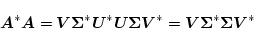 |
(2.649) |
になり
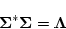 |
(2.650) |
ただし
![\begin{displaymath}
\mbox{\boldmath$\Lambda$}= \left[
\begin{array}{c\vert c}\L...
...t]
\quad\Lambda_1 = diag[\lambda_1,\lambda_2,\cdots,\lambda_r]
\end{displaymath}](img1417.png) |
(2.651) |
とおくと、(2.665)式を(2.664)式に代入して
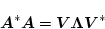 |
(2.652) |
となる。
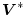 が正則のとき
が正則のとき
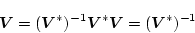 |
(2.653) |
の関係があるので
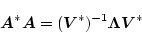 |
(2.654) |
より
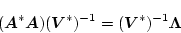 |
(2.655) |
となり、この
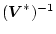 は対角化行列を、
は対角化行列を、
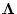 は
は
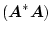 の固有値行列を意味する。したがって特異値
の固有値行列を意味する。したがって特異値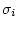 は
は
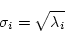 |
(2.656) |
より求めることが出来る。
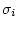 の最大値
の最大値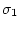 を
を
 、最小値
、最小値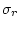 を
を
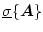 で表し
で表し
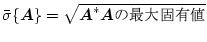 |
|
|
|
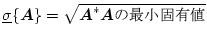 |
|
|
(2.657) |
で定義する。この特異値には次のような性質を有する。
- P1)
-
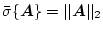 でユークリッド・ベクトル・ノルム
から誘導された行列ノルムである。
でユークリッド・ベクトル・ノルム
から誘導された行列ノルムである。
- P2)
-
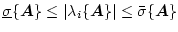
ただし
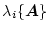 は
は
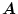 の固有値を意味する。
の固有値を意味する。
- P3)
-
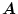 が正方で、
が正方で、
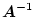 が存在するとき
が存在するとき
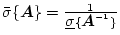
- P4)
-
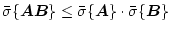
- P5)
-
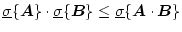
- P6)
-
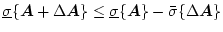
閉ループ系が開ループ系より感度が減少する条件は(2.626)式の還送差を
用いた場合、(2.642)式より
![\begin{displaymath}[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(-j\omega)\mbox{\bol...
...(j\omega)\mbox{\boldmath$F$}(j\omega)] \ge \mbox{\boldmath$Z$}
\end{displaymath}](img1439.png) |
(2.658) |
であるが、
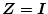 のとき
のとき
![\begin{displaymath}[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(-j\omega)\mbox{\bol...
...(j\omega)\mbox{\boldmath$F$}(j\omega)] \ge \mbox{\boldmath$I$}
\end{displaymath}](img1441.png) |
(2.659) |
になる。この式で
![\begin{displaymath}
\mbox{\boldmath$A$} = [\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(j\omega)\mbox{\boldmath$F$}(j\omega)]
\end{displaymath}](img1442.png) |
(2.660) |
と考えれば
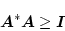 |
(2.661) |
を意味し、したがってこの十分条件は
すなわち
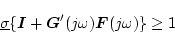 |
(2.662) |
になる。これが閉ループ系が開ループ系より感度が
減少するための特異値による条件式である。この特異値は周波数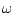 の関数であり、全周波数範囲にわたってこの条件を満足することは難しいが、実際的に有用な周波数範囲でこの条件を満足すれば十分差仕えない。
の関数であり、全周波数範囲にわたってこの条件を満足することは難しいが、実際的に有用な周波数範囲でこの条件を満足すれば十分差仕えない。
いまパラメータ変動を
- (A)加法的摂動
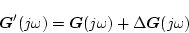 |
(2.663) |
- (B)乗法的摂動
-
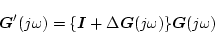 |
(2.664) |
の二種類に分けて考える。
- (A)の場合
- (2.677)式の左辺に、(2.678)式および特異値の性質P6,P4を適用すると
となるから、(2.677)式の十分条件は
| |
|
![$\displaystyle \underline{\sigma}[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\omeg...
...lta\mbox{\boldmath$G$}(j\omega)]\cdot\bar{\sigma}[\mbox{\boldmath$F$}(j\omega)]$](img1452.png) |
|
| |
|
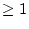 |
(2.666) |
になる。これを書き換えると
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)]\leq\frac{\u...
...h$F$}(j\omega)]-1}{\bar{\sigma}[\mbox{\boldmath$F$}(j\omega)]}
\end{displaymath}](img1454.png) |
(2.667) |
のようになり、感度減少の条件式である。
- (B)の場合
- (2.677)式の左辺に(2.679)式および特異値の性質P5,P6を適用すると
になるから、(2.677)式の十分条件は
| |
|
![$\displaystyle \{\underline{\sigma}[\mbox{\boldmath$I$}+\{\mbox{\boldmath$G$}(j\...
...]\}\underline{\sigma}[\mbox{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)]$](img1459.png) |
|
| |
|
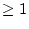 |
(2.668) |
となる。これを書き換え、特異値の性質P3を適用すると
になり、さらに
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)]\leq\underli...
...box{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)\}^{-1}]
\end{displaymath}](img1462.png) |
(2.670) |
となって、(B)の場合の感度減少の条件式になる。(2.683)、(2.686)式とも左辺は変動分のみであるから、この値が右辺の値以下の範囲において感度減少することを意味してる。しかしながら、両辺の誘導に際して不等式の関係を用いており、十分条件であるため、相当余裕がある。そのためこの条件式は保守的
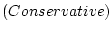 であるといわれている。
であるといわれている。
図 2.37:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-2.eps} \end{center} \end{figure}](img1464.png) |
図2.37は
に関して(2.686)式の関係(この場合
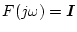 )を示したもので、
約
)を示したもので、
約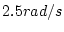 以下の範囲で条件を満たしていることがわかる。
以下の範囲で条件を満たしていることがわかる。
パラメータ変動が小さいときは(2.638)式で示したように還送差を
![$[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(s)\mbox{\boldmath$F$}(S)]$](img1486.png) とおけるので、感度条件は(2.677)式の代わりに
とおけるので、感度条件は(2.677)式の代わりに
![\begin{displaymath}
\underline{\sigma} [\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)] \ge 1
\end{displaymath}](img1487.png) |
(2.672) |
として扱うことができる。



Next: 特異値による安定性の解析
Up: ロバスト制御 (Robust Control)
Previous: システム感度(Sensitivity)
Yasunari SHIDAMA
平成15年5月12日
![]() の転置行列を
の転置行列を
![]() 、共役行列を
、共役行列を
![]() としたとき、
としたとき、
![]() に対し、その共役転値行列を
に対し、その共役転値行列を
![]() としたとき、
としたとき、
![]() が
が![]() の行列で、
の行列で、
![]() のとき、
のとき、
![]() の固有値を
の固有値を
![]() とすると、
とすると、
![]() は正の実数ゆえ
は正の実数ゆえ
![]() はそれぞれ
はそれぞれ
![]() の最大値
の最大値![]() を
を
![]() 、最小値
、最小値![]() を
を
![]() で表し
で表し
![]() とおけるので、感度条件は(2.677)式の代わりに
とおけるので、感度条件は(2.677)式の代わりに