


Next: 安定性と感度減少との相反性
Up: ロバスト制御 (Robust Control)
Previous: 特異値による感度解析
安定な一巡伝達関数
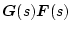 を持つ系が、閉ループにしたときも
安定であるための必要十分条件は、偏角の原理より、その還送差行列の行列式
を持つ系が、閉ループにしたときも
安定であるための必要十分条件は、偏角の原理より、その還送差行列の行列式
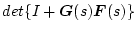 のナイキスト線図が原点を廻らないことである。
のナイキスト線図が原点を廻らないことである。
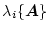 を
を
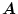 の固有値とすると
の固有値とすると
![\begin{displaymath}
det\{\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(s)\mbox{\boldma...
...}[1+\lambda_i\{\mbox{\boldmath$G$}(s)\mbox{\boldmath$F$}(s)\}]
\end{displaymath}](img1490.png) |
(2.673) |
と表すことができ、
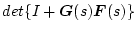 が原点を廻る回数は
が原点を廻る回数は
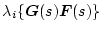 のナイキスト線図が(−1、0)の回りを廻る回数
の和となる。もしすべての
のナイキスト線図が(−1、0)の回りを廻る回数
の和となる。もしすべての
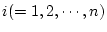 に対して
に対して
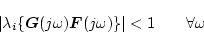 |
(2.674) |
の関係があれば、
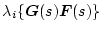 のナイキスト線図は(−1,0)
を廻らず安定である。その十分条件は特異値を用いて
のナイキスト線図は(−1,0)
を廻らず安定である。その十分条件は特異値を用いて
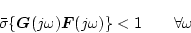 |
(2.675) |
で表現される。パラメータ変動後の閉ループ系に関しては
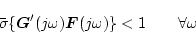 |
(2.676) |
で表される。パラメータ変動が小さくて連続的な場合は、前述したように(2.692)式で近似して扱うことができる。
パラメータ変動が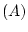 加法的摂動の場合、
加法的摂動の場合、
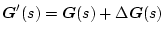 ゆえ
ゆえ
![$\displaystyle det\{\mbox{\boldmath$I$}+\mbox{\boldmath$G$}'(s)\mbox{\boldmath$F...
...+\{\mbox{\boldmath$G$}(s)+\Delta\mbox{\boldmath$G$}(s)\}\mbox{\boldmath$F$}(s)]$](img1498.png) |
|
|
|
![$\displaystyle =det[\mbox{\boldmath$I$}+\Delta\mbox{\boldmath$G$}(s)\mbox{\boldm...
...^{-1}]det\{
\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(s)\mbox{\boldmath$F$})(s)\}$](img1499.png) |
|
|
(2.677) |
と書ける。ノミナル時の閉ループが安定であれば、
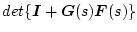 のナイキスト線図は原点をイ廻らないから、パラメータ変動後の
閉ループが安定なための十分条件は
のナイキスト線図は原点をイ廻らないから、パラメータ変動後の
閉ループが安定なための十分条件は
![\begin{displaymath}
\vert\lambda_i[\Delta\mbox{\boldmath$G$}(s)\mbox{\boldmath$F...
...+\mbox{\boldmath$G$}(s)\mbox{\boldmath$F$}(s)\}^{-1}]\vert < 1
\end{displaymath}](img1501.png) |
(2.678) |
となる。これを特異値を用いて表現すると
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)\mbox{\boldma...
...\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)\}^{-1}] < 1
\end{displaymath}](img1502.png) |
(2.679) |
となり、特異値の性質P4)を用いて
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)]\cdot\bar{\s...
...x{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)]^{-1} < 1
\end{displaymath}](img1503.png) |
(2.680) |
と書け、さらに特異値の性質P3)を用いて
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)]\cdot\bar{\s...
...$I$}+\mbox{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)]
\end{displaymath}](img1504.png) |
(2.681) |
が十分条件となる。
この式はスカラの場合は
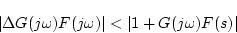 |
(2.682) |
と書ける。これは図2.38からもわかるように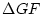 の長さが
の長さが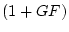 の長さより短ければ、−1を廻らないことを意味している。
の長さより短ければ、−1を廻らないことを意味している。
図 2.38:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-3.eps} \end{center} \end{figure}](img1508.png) |
パラメータ変動が(B)乗法
的摂動の場合、
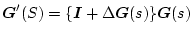 ゆえ
ゆえ
となり、同様にしてパラメータ変動後の閉ループの安定なための十分条件は、
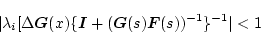 |
(2.684) |
になる。これより特異値で表現すると
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)\{\mbox{\bold...
...ath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega))^{-1}\}^{-1}] < 1
\end{displaymath}](img1514.png) |
(2.685) |
となって、この十分条件は
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)]\bar{\sigma}...
...ath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega))^{-1}\}^{-1}] < 1
\end{displaymath}](img1515.png) |
(2.686) |
さらに
![\begin{displaymath}
\bar{\sigma}[\Delta\mbox{\boldmath$G$}(j\omega)] <
\under...
...box{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)\}^{-1}]
\end{displaymath}](img1516.png) |
(2.687) |
を得る。
またパラメータ変動を(C)として
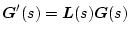 の形にした場合は、
の形にした場合は、
のようになり、
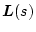 と
と
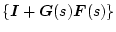 が正則であれば、パラメータ
変動後の閉ループが安定のための十分条件は
が正則であれば、パラメータ
変動後の閉ループが安定のための十分条件は
![\begin{displaymath}
\vert\lambda_i[\{\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\o...
...\{\mbox{\boldmath$L$}(j\omega)-\mbox{\boldmath$I$}\}]\vert < 1
\end{displaymath}](img1524.png) |
(2.689) |
で表現され、特異値を用いると
![\begin{displaymath}
\bar{\sigma}[\{\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\ome...
...\{\mbox{\boldmath$L$}^{-1}(j\omega)-\mbox{\boldmath$I$}\}] < 1
\end{displaymath}](img1525.png) |
(2.690) |
と書かれる。この十分条件も前と同様
![\begin{displaymath}
\bar{\sigma}[\{\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\ome...
...a}[\mbox{\boldmath$L$}^{-1}
(j\omega)-\mbox{\boldmath$I$}] < 1
\end{displaymath}](img1526.png) |
(2.691) |
![\begin{displaymath}
\bar{\sigma}[\mbox{\boldmath$L$}^{-1}(j\omega)-\mbox{\boldma...
...I$}+\mbox{\boldmath$G$}(j\omega)
\mbox{\boldmath$F$}(j\omega)]
\end{displaymath}](img1527.png) |
(2.692) |
になる。
いまもし
![\begin{displaymath}
\mbox{\boldmath$L$}= diag[K_{ii}e^{j\theta_{ii}}]
\end{displaymath}](img1528.png) |
(2.693) |
とすると、
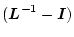 の各対角要素は
の各対角要素は
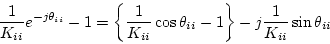 |
(2.694) |
になるので、これより
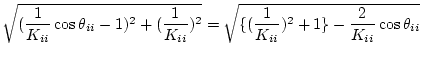 |
|
|
|
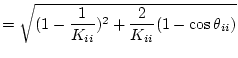 |
|
|
(2.695) |
の関係を得るので、(2.707)式は
![$\displaystyle \bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}] = \max_{1\le i \le n}\sqrt{(1-\frac{1}{K_{ii}})^2+
\frac{2}{K_{ii}}(1-\cos\theta_{ii})}$](img1533.png) |
|
|
|
![$\displaystyle \leq \underline{\sigma}[\mbox{\boldmath$I$}+\mbox{\boldmath$G$}(j\omega)\mbox{\boldmath$F$}(j\omega)]$](img1534.png) |
|
|
(2.696) |
のように書かれる。
この
![$\bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}]$](img1535.png) をゲイン
をゲイン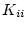 と位相
と位相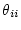 に対して
描くと図2.39のようになる。
に対して
描くと図2.39のようになる。
図 2.39:
![\begin{figure}\begin{center}
\psbox[scale=1.00]{eps/2-11-4.eps} \end{center} \end{figure}](img1538.png) |
この図は全入力系におけるゲインと位相の両方が同時に変化した場合、あるいは特定
の片方の値に対する他方の位相余裕あるいはゲイン余裕を求めるのに用いられる。
例えば、
![$\bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}]$](img1535.png) の値を
の値を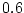 にとった場合、位相余裕
にとった場合、位相余裕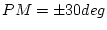 のとき、
ゲイン余裕
のとき、
ゲイン余裕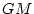 は
は
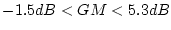 である。また
である。また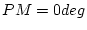 なら
なら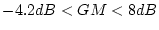 であり、
であり、
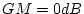 なら
なら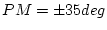 である。
である。
![$\bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}]=1$](img1547.png) の場合は、
の場合は、
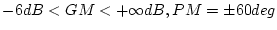 で安定余裕が非常に大きいことを意味する。
で安定余裕が非常に大きいことを意味する。
![$\bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}]=0.9$](img1549.png) では、
では、
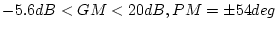 であり、サーボ
系の安定余裕の適当値
であり、サーボ
系の安定余裕の適当値
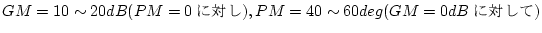 に大体適合している。
に大体適合している。
この
![$\bar{\sigma}[\mbox{\boldmath$L$}^{-1}-\mbox{\boldmath$I$}]=\underline{\sigma}_D$](img1552.png) としたとき、
としたとき、
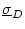 で定められた安定余裕をもつためには
で定められた安定余裕をもつためには
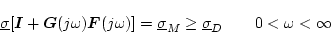 |
(2.697) |
でなければならない。これは図2.40に示す斜線の部分がなくなるように
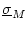 を
を
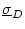 以上に押し上げることを意味している。
以上に押し上げることを意味している。
図 2.40:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-5.eps} \end{center} \end{figure}](img1556.png) |



Next: 安定性と感度減少との相反性
Up: ロバスト制御 (Robust Control)
Previous: 特異値による感度解析
Yasunari SHIDAMA
平成15年5月12日
![]() を持つ系が、閉ループにしたときも
安定であるための必要十分条件は、偏角の原理より、その還送差行列の行列式
を持つ系が、閉ループにしたときも
安定であるための必要十分条件は、偏角の原理より、その還送差行列の行列式
![]() のナイキスト線図が原点を廻らないことである。
のナイキスト線図が原点を廻らないことである。
![]() を
を
![]() の固有値とすると
の固有値とすると
![]() 加法的摂動の場合、
加法的摂動の場合、
![]() ゆえ
ゆえ
![]() ゆえ
ゆえ
![]() の形にした場合は、
の形にした場合は、
![]() をゲイン
をゲイン![]() と位相
と位相![]() に対して
描くと図2.39のようになる。
に対して
描くと図2.39のようになる。
![]() の値を
の値を![]() にとった場合、位相余裕
にとった場合、位相余裕![]() のとき、
ゲイン余裕
のとき、
ゲイン余裕![]() は
は
![]() である。また
である。また![]() なら
なら![]() であり、
であり、
![]() なら
なら![]() である。
である。
![]() の場合は、
の場合は、
![]() で安定余裕が非常に大きいことを意味する。
で安定余裕が非常に大きいことを意味する。
![]() では、
では、
![]() であり、サーボ
系の安定余裕の適当値
であり、サーボ
系の安定余裕の適当値
![]() に大体適合している。
に大体適合している。
![]() としたとき、
としたとき、
![]() で定められた安定余裕をもつためには
で定められた安定余裕をもつためには