

Next: LTR(Loop Transfer Recovery)
Up: ���o�X�g���� �iRobust Control�j
Previous: ���萫�Ɗ��x�����Ƃ̑�����
��ʂɓ`�B���s��Ȃǂ́A����A���q���ɂ��̑��������\������镪���`�ɂȂ��Ă���B
������`�łȂ��������s��ɕ��������ĕ\��������@���s��\���Ƃ����B
�^����ꂽ�����`�̍s��
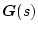 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A
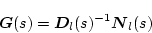 |
(2.703) |
���������A
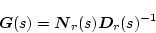 |
(2.704) |
���E�����Ƃ����B������
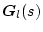 �A
�A
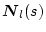 �݂͌��ɍ��f�́A
�݂͌��ɍ��f�́A
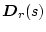 �A
�A
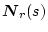 �݂͌��ɉE�f�̑������s��ł���B
�݂͌��ɉE�f�̑������s��ł���B
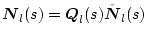 �A
�A
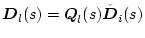 �Ƃ����悤�ɁA
�Ƃ����悤�ɁA
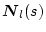 �A
�A
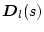 �̍����̋��ʈ��q
�̍����̋��ʈ��q
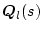 ��
���j���W�����s��i�t�s���݂���s��j�Ɍ�����Ƃ����f�Ƃ����B
��
���j���W�����s��i�t�s���݂���s��j�Ɍ�����Ƃ����f�Ƃ����B
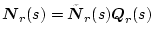 �A
�A
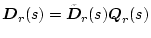 �Ɋւ��ē��l�̏ꍇ�E�f�Ƃ����B
�Ɋւ��ē��l�̏ꍇ�E�f�Ƃ����B
�^����ꂽ �̍s��
�̍s��
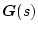 �ɑ�������i
�ɑ�������i �j�������s��
�菇�͎��̂Ƃ���ł���B
�j�������s��
�菇�͎��̂Ƃ���ł���B
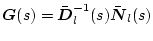
�����߂�B������
![$\bar{\mbox{\boldmath$D$}}_l(s) = diag[d_1,d_2,\cdots,d_m]$](img1599.png) �Ƃ���B
�Ƃ���B
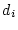 ��
��
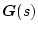 ��
��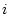 �s�̗v�f�̕���̍ŏ����{�������ł���B
�s�̗v�f�̕���̍ŏ����{�������ł���B
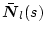 ��
��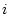 �s��
�s��
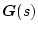 ��
��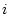 �s��
�s��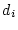 ���|�������̂ł���B
���|�������̂ł���B
 �s��
�s��
![$[\bar{\mbox{\boldmath$D$}}_l(s):\bar{\mbox{\boldmath$N$}}_l(S)]$](img1603.png) ����{��ϊ��ɂ�ĉ��O�p�s��
�A���Ȃ킿
����{��ϊ��ɂ�ĉ��O�p�s��
�A���Ȃ킿
![$[\mbox{\boldmath$P$}(s):0]$](img1604.png) �ɕϊ�����B
���̂Ƃ�
�ɕϊ�����B
���̂Ƃ�
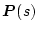 ��
��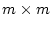 �̍s��ł���A
�̍s��ł���A
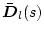 ��
��
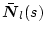 �̍����ʈ��q�i
�̍����ʈ��q�i
 �j�ɂȂ��Ă���B
�j�ɂȂ��Ă���B
3
20D
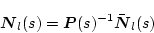 |
(2.705) |
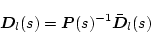 |
(2.706) |
���
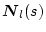 �A
�A
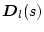 �����߂���B
�����߂���B
���������̊����͗B��ł͂Ȃ��B
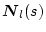 �A
�A
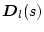 �ɍ�����C�ӂ�
���j���W�����ȍs����|�������̂������ɂȂ�B
�ɍ�����C�ӂ�
���j���W�����ȍs����|�������̂������ɂȂ�B
�Ȃ�
 �ɂ������{��ϊ��ɂ�艺�O�p�s��ւ̕ϊ��͎��̕��@�ŋ��߂���B
�ɂ������{��ϊ��ɂ�艺�O�p�s��ւ̕ϊ��͎��̕��@�ŋ��߂���B
���Ȃ킿
![\begin{displaymath}[\bar{\mbox{\boldmath$D$}}_l(s):\bar{\mbox{\boldmath$N$}}_l(s...
...\\
a_{m1} & a_{m2} & \cdots & a_{n(m+r)}
\end{array}\right]
\end{displaymath}](img1611.png) |
(2.707) |
�ɂ�����
�i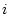 �j���s
�j���s
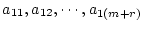 �̂����O�ȊO�ł��̍Œ���̂���
��
�̂����O�ȊO�ł��̍Œ���̂���
��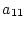 �̏��ɗ���悤�ɗ��ϊ�����B
�̏��ɗ���悤�ɗ��ϊ�����B
�i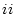 �j�V����
�j�V����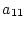 �ɓK���Ȃ��̑��������|���āA
�ɓK���Ȃ��̑��������|���āA
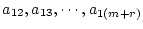 ����������Ƃɂ��A
����������Ƃɂ��A
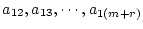 �̎�����
�̎�����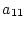 �̎���
���Ⴍ�Ȃ�悤�ɂ���B�i�������͕s�j
�̎���
���Ⴍ�Ȃ�悤�ɂ���B�i�������͕s�j
�i �j
�j
 �����ׂĂO�ƂȂ�܂Łi
�����ׂĂO�ƂȂ�܂Łi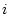 �j�i
�j�i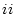 �j
���J��Ԃ��B
�j
���J��Ԃ��B
�i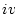 �j���̌�A�i2.724�j���̈�s����������
�j���̌�A�i2.724�j���̈�s����������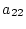 ������[�Ƃ��鏬�s��ɂ���
��L�́i
������[�Ƃ��鏬�s��ɂ���
��L�́i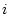 �j
�j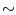 �i
�i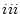 �j���J��Ԃ��B
���̏ꍇ
�j���J��Ԃ��B
���̏ꍇ
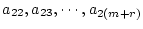 ���i
���i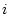 �j��
�j��
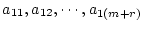 �Ƒz�肵�čs���B
�Ƒz�肵�čs���B
�i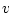 �j�i
�j�i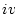 �j���I�������A
�j���I�������A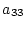 ������[�Ƃ��镔���ɂ��ē��l�̂��Ƃ��s���B
�ȉ����l�ɂ��ĕϊ�����������B
������[�Ƃ��镔���ɂ��ē��l�̂��Ƃ��s���B
�ȉ����l�ɂ��ĕϊ�����������B
�u��v
![\begin{displaymath}
\mbox{\boldmath$G$}(s) =
\left[ \begin{array}{cc}
\frac{s-1}...
...rac{2}{s}\\
\frac{2s-1}{s^2} & \frac{2}{s}
\end{array}\right]
\end{displaymath}](img1620.png) |
(2.708) |
�̍��������s���B
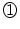 �@
�@
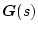 �̂P�s�ڂ̕���
�̂P�s�ڂ̕���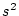 ��
��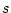 �Ƃ̍ŏ����{��������
�Ƃ̍ŏ����{��������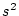 �ł���A
�Q�s�ڂ����l�ɂ���
�ł���A
�Q�s�ڂ����l�ɂ���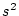 �䂦
�䂦
![\begin{displaymath}
\bar{\mbox{\boldmath$D$}}_l(s)= diag[s^2 s^2]
\end{displaymath}](img1621.png) |
(2.709) |
�Ƃ���B
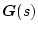 �̂P�s�ڂ�
�̂P�s�ڂ�
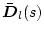 �̂P�A�P�v�f
�̂P�A�P�v�f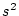 ���Q�s�ڂ�
���Q�s�ڂ�
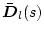 �̂Q�A�Q�v�f
�̂Q�A�Q�v�f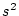 ���|����
���|����
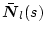 �����߂��
�����߂��
![\begin{displaymath}
\bar{\mbox{\boldmath$N$}}_l(s)=
\left[ \begin{array}{cc}
s-1 & 2s\\
2s-1 & 2s
\end{array}\right]
\end{displaymath}](img1622.png) |
(2.710) |
�ƂȂ�B
![\begin{displaymath}[\bar{\mbox{\boldmath$D$}}_l(s):\bar{\mbox{\boldmath$N$}}_l(s...
...c}
s^2 & 0 & s-1 & 2s\\
0 & s^2& 2s-1 & 2s
\end{array}\right]
\end{displaymath}](img1623.png) |
(2.711) |
����{��ϊ����s�����O�p�s��ɂ���B
![$\left[ \begin{array}{cccc}
s^2 & 0 & s-1 & 2s\\
0 & s^2& 2s-1 & 2s
\end{array} \right]$](img1624.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j�Ɓi�S��j������..
...begin{array}{cccc}
s & 0 & s-1 & s^2\\
s & s^2& 2s-1 & 0
\end{array} \right]$](img1625.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j-�i�P��j�����...
...begin{array}{cccc}
s & 0 & -1 & 0 \\
s & s^2& s-1 & -s^2
\end{array} \right]$](img1626.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j�Ɓi�R��j������..
...begin{array}{cccc}
-1 & 0 & s & 0 \\
s-1 & s^2& s & -s^2
\end{array} \right]$](img1627.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j+3\times�i�P����..
...gin{array}{cccc}
-1 & 0 & 0 & 0 \\
s-1 & s^2& s^2 & -s^2
\end{array} \right]$](img1628.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j-�i�Q��j�A�i�S...
...]
\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j\times (-1)}}$](img1629.png)
![$\left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
1-s & s^2 & 0 & 0
\end{array} \right]
= [\mbox{\boldmath$P$}(s):0]$](img1630.png) �ƂȂ�B
�ƂȂ�B
![\begin{displaymath}
\mbox{\boldmath$P$}^{-1}(s)=
\left[ \begin{array}{cc}
1 &0 \...
...\left[ \begin{array}{cc}
s^2 &0 \\
s-1 &1
\end{array} \right]
\end{displaymath}](img1632.png) |
(2.712) |
���
![\begin{displaymath}
\mbox{\boldmath$D$}_l(s)=\mbox{\boldmath$P$}^{-1}(s)\bar{\mb...
...\left[ \begin{array}{cc}
s^2 &0 \\
s-1 &1
\end{array} \right]
\end{displaymath}](img1633.png) |
(2.713) |
![$\displaystyle \mbox{\boldmath$N$}_l(s)=\mbox{\boldmath$P$}^{-1}(s)\bar{\mbox{\b...
...{array} \right]
\left[ \begin{array}{cc}
s-1 &2s\\
2s-1&2s
\end{array} \right]$](img1634.png) |
|
|
|
![$\displaystyle =\left[ \begin{array}{cc}
s-1 &2s \\
1 &2
\end{array} \right]$](img1635.png) |
|
|
(2.714) |
��B�䂦��
![\begin{displaymath}
\mbox{\boldmath$G$}(s)=
\left[ \begin{array}{cc}
s^2 &0 \\
...
...}
\left[ \begin{array}{cc}
s-1 &2s\\
1 &2
\end{array} \right]
\end{displaymath}](img1636.png) |
(2.715) |
�̂悤�ɍs�����ꂽ�B
�E�����̏ꍇ���ގ��̕��@�ōs�����Ƃ��ł���B
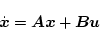 |
(2.716) |
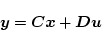 |
(2.717) |
�Ƃ����V�X�e���́A�`�B���ŕ\�������
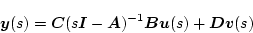 |
(2.718) |
�Ə�����B�������A
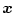 ��
��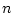 ���A
���A
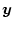 ��
��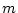 ���A
���A
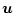 ��
��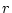 ���A
���A
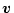 ��
��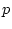 ���Ƃ���B
���Ƃ���B
![\begin{displaymath}[\mbox{\boldmath$C$}(s\mbox{\boldmath$I$}-\mbox{\boldmath$A$}...
...1}_p(s)[\mbox{\boldmath$N$}_1(s)\vert\mbox{\boldmath$N$}_2(s)]
\end{displaymath}](img1641.png) |
(2.719) |
�̂悤�ɍs��������B����
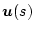 �A�O��
�A�O��
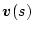 �����ꂼ�ꂻ�̏����l��
����
�����ꂼ�ꂻ�̏����l��
����
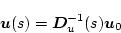 |
(2.720) |
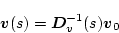 |
(2.721) |
�Ƃ���ƁA�V�X�e���͐}2.42�̎����Ŏ������悤�ɕ\�����B
�} 2.42:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-7.eps} \end{center} \end{figure}](img1646.png) |
�p�����[�^���ϓ����Ă����������ς�炸�܂��O������������ێ�����悤�Ȑ���n
�Ƃ��āA�}2.42�ɔj���Ŏ����悤�Ȓ����t�B�[�h�o�b�N�ƑO�u�⏞��
 ��
�t������B���̂Ƃ��A
��
�t������B���̂Ƃ��A
 ��
�� ���ł���A
���ł���A
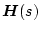 ��
�� �̗L����
�ł���B�}2.42���
�̗L����
�ł���B�}2.42���
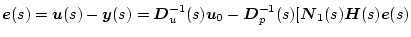 |
|
|
|
![$\displaystyle +\mbox{\boldmath$N$}_2(s)\mbox{\boldmath$D$}^{-1}_v(s)\mbox{\boldmath$v$}_0]$](img1649.png) |
|
|
(2.722) |
�ɂȂ�A����������
![\begin{displaymath}
\mbox{\boldmath$e$}(s)=\{\mbox{\boldmath$D$}_p(s)+\mbox{\bol...
...{\boldmath$u$}_0 \\
\mbox{\boldmath$v$}_0
\end{array} \right]
\end{displaymath}](img1650.png) |
(2.723) |
�ƂȂ�B�㎮����
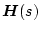 ��K�ɑI�����邱�Ƃɂ��A����������ێ����A
��K�ɑI�����邱�Ƃɂ��A����������ێ����A
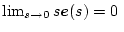 �Ƃ��邱�Ƃ��ł���Ȃ�A�Q�ߒǐ������ƊO�����������������邱�ƂɂȂ�B
�Ƃ��邱�Ƃ��ł���Ȃ�A�Q�ߒǐ������ƊO�����������������邱�ƂɂȂ�B
���㎮����
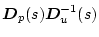 �����
�����
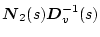 �ɑ�
�������������
�ɑ�
�������������
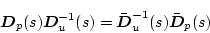 |
(2.724) |
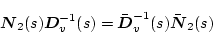 |
(2.725) |
�Ƃ����ꍇ�A�i2.740�j����
![\begin{displaymath}
\mbox{\boldmath$e$}(s)=\{\mbox{\boldmath$D$}_p(s)+\mbox{\bol...
...{\boldmath$u$}_0 \\
\mbox{\boldmath$v$}_0
\end{array} \right]
\end{displaymath}](img1650.png) |
(2.726) |
�̂悤�ɏ�����B
����ɂ�����
![$[\bar{\mbox{\boldmath$D$}}^{-1}_u(s)\bar{\mbox{\boldmath$D$}}_p(s)\vert\bar{\mbox{\boldmath$D$}}^{-1}_v
\bar{\mbox{\boldmath$N$}}_2(s)]$](img1656.png) �ɑ��č�����������
�ɑ��č�����������
![\begin{displaymath}[\bar{\mbox{\boldmath$D$}}^{-1}_u(s)\bar{\mbox{\boldmath$D$}}...
...{-1}(s)[\mbox{\boldmath$M$}_1(s)\vert\mbox{\boldmath$M$}_2(s)]
\end{displaymath}](img1657.png) |
(2.727) |
�Ƃ���ƁA�i2.743�j����
![\begin{displaymath}
\mbox{\boldmath$e$}(s)=\{\mbox{\boldmath$D$}_p(s)+\mbox{\bol...
...{\boldmath$u$}_0 \\
\mbox{\boldmath$v$}_0
\end{array} \right]
\end{displaymath}](img1650.png) |
(2.728) |
�ɂȂ�B����
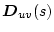 ��
��
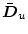 ��
��
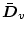 �̍��ŏ����{�s���
�Ȃ��Ă���B���������ē��͂ƊO���ɑ��ċ��ʂ̕���s������`�ł���B
�̍��ŏ����{�s���
�Ȃ��Ă���B���������ē��͂ƊO���ɑ��ċ��ʂ̕���s������`�ł���B
����
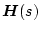 ���s������
���s������
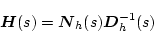 |
(2.729) |
�Ƃ���ƁA������i2.745�j���ɑ�����Ď�����B
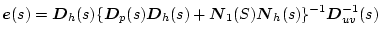 |
|
|
|
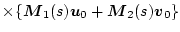 |
|
|
(2.730) |
�������[�v������Ȃ�
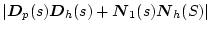 �̗�_��
���̎��������B
�̗�_��
���̎��������B
���
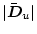 ��
��
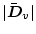 �Ƃ̍ŏ����{����
�Ƃ̍ŏ����{����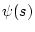 �Ƃ���B
�����
�Ƃ���B
�����
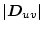 �Ƃ��������B�܂�
�Ƃ��������B�܂�
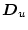 �y��
�y��
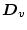 �̓p�����[�^�ϓ����Ȃ����̂Ƃ��A
���̂Ƃ�
�̓p�����[�^�ϓ����Ȃ����̂Ƃ��A
���̂Ƃ�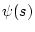 ���ϓ����Ȃ��B
���ϓ����Ȃ��B
����
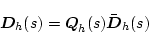 |
(2.731) |
�Ƃ��A
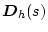 ��
��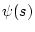 �Ŋ�����悤��
�Ŋ�����悤��
![$\mbox{\boldmath$Q$}_h(s)=diag[\psi (s)]$](img1673.png) ��
�Ƃ�B���̂Ƃ��i2.747�j���ɂ����āA
��
�Ƃ�B���̂Ƃ��i2.747�j���ɂ����āA
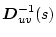 �̕��ꐬ����
�̕��ꐬ����
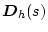 ����
����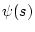 �Ƒł��������̂�
�Ƒł��������̂�
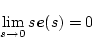 |
(2.732) |
�ƂȂ�B
����
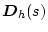 �i����������
�i����������
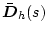 �j��
�j��
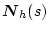 ��
��
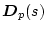 �����
�����
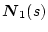 ���ϓ����Ă�
���ϓ����Ă�
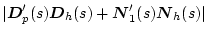 �̗�_�����̎����������A���̍s��������ۂ悤�ɑI�肷��Ȃ��
�A�p�����[�^���ϓ����Ă�
�̗�_�����̎����������A���̍s��������ۂ悤�ɑI�肷��Ȃ��
�A�p�����[�^���ϓ����Ă�
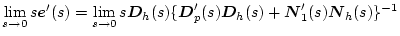 |
|
|
|
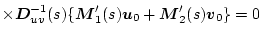 |
|
|
(2.733) |
�̂悤�ɂȂ�A�Q�ߒǐ������ƊO������������ۂ��Ă���A���o�X�g�ł���B
�u���v���܃v�����g��
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}=
\left[ \begin{array}{cc}
1 &-1 \\...
...y}{cc}
1 & 2 \\
2 & 2
\end{array} \right]
\mbox{\boldmath$u$}
\end{displaymath}](img1683.png) |
(2.734) |
![\begin{displaymath}
\mbox{\boldmath$y$}=
\left[ \begin{array}{cc}
1 & 0 \\
0 & ...
...gin{array}{c}
1 \\
2
\end{array} \right]
\mbox{\boldmath$v$}
\end{displaymath}](img1684.png) |
(2.735) |
�Ƃ���B�����`�B���̌`�ŕ\�������
![\begin{displaymath}
\mbox{\boldmath$y$}(s)=
\left[ \begin{array}{cc}
\frac{s-1}{...
...(s)+
\left[ \begin{array}{c}
1 \\
2
\end{array} \right]
v(s)
\end{displaymath}](img1685.png) |
(2.736) |
�ɂȂ�B����
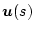 �ƊO��
�ƊO��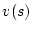 �����ꂼ��
�����ꂼ��
![\begin{displaymath}
\left.\begin{array}{rcl}
\mbox{\boldmath$u$}(s) & = & [\fr...
...]^T \\
v(s) & = & \frac{1}{s^2(s+1)}v_0
\end{array}\right\}
\end{displaymath}](img1687.png) |
(2.737) |
�Ƃ���B���̂Ƃ�
![\begin{displaymath}[\mbox{\boldmath$C$}(s\mbox{\boldmath$I$}-\mbox{\boldmath$A$}...
...& 1 \\
\frac{2s-1}{s^2} & \frac{2}{s} & 2
\end{array} \right]
\end{displaymath}](img1688.png) |
(2.738) |
�ł��邩��
![\begin{displaymath}
\bar{\mbox{\boldmath$D$}}_l(s)=diag[s^2 \; s^2]
\end{displaymath}](img1689.png) |
(2.739) |
�ɂƂ��
![\begin{displaymath}
\bar{\mbox{\boldmath$N$}}_l(s)=
\left[ \begin{array}{ccc}
s-1 & 2s & s^2 \\
2s-1 & 2s & 2s^2
\end{array} \right]
\end{displaymath}](img1690.png) |
(2.740) |
�ɂȂ�̂ŁA
![$\mbox{\boldmath$P$}(s)=
\left[ \begin{array}{cc}
1 & 0 \\
1-s & s^2
\end{array} \right]$](img1693.png)
�ɂƂ��
![\begin{displaymath}
\mbox{\boldmath$D$}_l(s)=
\left[ \begin{array}{cc}
1 & 0 ...
...eft[ \begin{array}{cc}
s^2 & 0 \\
s-1 & 1
\end{array} \right]
\end{displaymath}](img1694.png) |
(2.741) |
![\begin{displaymath}
\mbox{\boldmath$N$}_l(s)=
\left[ \begin{array}{cc}
1 & 0 ...
...rray}{ccc}
s-1 & 2s & s^2 \\
1 & 2 & s+1
\end{array} \right]
\end{displaymath}](img1695.png) |
(2.742) |
�������邪�A����ɑO���烆�j���W�����X�s����|����
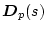 �A
�A
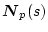 �����߂��
�����߂��
![\begin{displaymath}
\mbox{\boldmath$D$}_p(s)=
\left[ \begin{array}{cc}
0 & 1 ...
...left[ \begin{array}{cc}
s-1 & 1 \\
-s & s
\end{array} \right]
\end{displaymath}](img1697.png) |
(2.743) |
![\begin{displaymath}
\mbox{\boldmath$N$}_p(s)=
\left[ \begin{array}{cc}
0 & 1 ...
...in{array}{ccc}
1 & 2 & s+1 \\
1 & 0 & s
\end{array} \right]
\end{displaymath}](img1698.png) |
(2.744) |
�������A������
![\begin{displaymath}
\mbox{\boldmath$N$}_1(s)=
\left[ \begin{array}{cc}
1 & 2 ...
...$}_2(s)=
\left[ \begin{array}{c}
s+1 \\
s
\end{array} \right]
\end{displaymath}](img1699.png) |
(2.745) |
�@�@�@
�ƂȂ�A
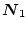 �͒萔�s��ƂȂ�B
�͒萔�s��ƂȂ�B
�܂��i2.764�j�����
![\begin{displaymath}
\mbox{\boldmath$D$}_u(s)=
\left[ \begin{array}{cc}
s & 0 \\
0 & s
\end{array} \right],�@�@�@
\mbox{\boldmath$D$}_v=s^2(s+1)
\end{displaymath}](img1701.png) |
(2.746) |
�ł��邱�Ƃ��킩��B�i2.741�j���A�i2.742�j���ɓK�p����
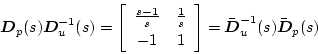 |
(2.747) |
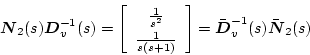 |
(2.748) |
���A
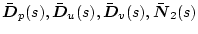 �����߂��
�����߂��
![$\bar{\mbox{\boldmath$D$}}_p(s)=
\left[ \begin{array}{cc}
s-1 & 1 \\
-s & 0
\en...
...ldmath$D$}}_u(s)=
\left[ \begin{array}{cc}
s & 0 \\
-s & 1
\end{array} \right]$](img1705.png)
![$\bar{\mbox{\boldmath$D$}}_v(s)=
\left[ \begin{array}{cc}
s^2 & 0 \\
-s & (s+1)...
...{\mbox{\boldmath$N$}}_2(s)=
\left[ \begin{array}{c}
1 \\
0
\end{array} \right]$](img1706.png)
��������B�܂�������p���āi2.744�j�����
![\begin{displaymath}
\mbox{\boldmath$D$}_{uv}(s)=
\left[ \begin{array}{cc}
s^2 & 0 \\
-s & (s+1)
\end{array} \right]
\end{displaymath}](img1707.png) |
(2.749) |
![\begin{displaymath}
\mbox{\boldmath$M$}_1(s)=
\left[ \begin{array}{cc}
+s(s-1) &...
...M$}_2(s)=
\left[ \begin{array}{c}
-1 \\
0
\end{array} \right]
\end{displaymath}](img1708.png) |
(2.750) |
��������B
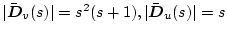 �䂦���̍ŏ����{����
�䂦���̍ŏ����{����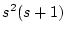 �ł���A�����
�ł���A�����
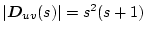 �Ƃ��������B����������
�Ƃ��������B����������
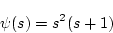 |
(2.751) |
![\begin{displaymath}
\mbox{\boldmath$Q$}_h(s)=diag[s^2(s+1), s^2(s+1)]
\end{displaymath}](img1713.png) |
(2.752) |
�Ƃ���B
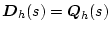 �ɂƂ��
�ɂƂ��
![$\displaystyle \mbox{\boldmath$D$}_p(s)\mbox{\boldmath$D$}_h(s)=
\left[ \begin{a...
...ght]
\left[ \begin{array}{cc}
s^2(s+1) & 0 \\
0 & s^2(s+1)
\end{array} \right]$](img1715.png) |
|
|
|
![$\displaystyle =
\left[ \begin{array}{cc}
s^4-s^2 & s^3+s^2 \\
-s^4-s^3 & s^4+s^3
\end{array} \right]$](img1716.png) |
|
|
(2.753) |
�ƂȂ�B
����
![\begin{displaymath}
\mbox{\boldmath$N$}_h(s)=
\left[ \begin{array}{cc}
\frac{146...
...rac{167}{42} & -\frac{21}{2}s+\frac{21}{2}
\end{array} \right]
\end{displaymath}](img1717.png) |
(2.754) |
�ɂƂ��
�ɂȂ�A������
![$\displaystyle [\mbox{\boldmath$D$}_p(s)\mbox{\boldmath$D$}_h(s)+\mbox{\boldmath$N$}_1(s)\mbox{\boldmath$N$}_h(s)] �@�@�@�@�@�@�@�@�@�@$](img1722.png) |
|
|
|
![$\displaystyle =
\left[ \begin{array}{cc}
s^4+6s^3-s^2-\frac{8}{21}s-\frac{1}{21...
...frac{1462}{21}s^2-\frac{3823}{21}s-8 & s^4+s^3+21s^2-21 \\
\end{array} \right]$](img1723.png) |
|
|
(2.756) |
�������A�㎮�̍s��
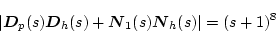 |
(2.757) |
�ƂȂ��āA���̍���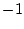 �Ƃ������荪�ɂȂ�B
�Ƃ������荪�ɂȂ�B
�p�����[�^���ϓ����Ă��A���̍��������ۂ��Ă���Ȃ�A
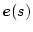 �̍ŏI�l��
�̍ŏI�l��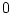 �ƂȂ�A
�����͐����Ȃ��B
�ƂȂ�A
�����͐����Ȃ��B
�Ȃ��A�i2.772�j����
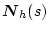 �͐�Ɂi2.775�j����
�悤�Ɉ��荪��^���Ă����āA������t�Z���ċ��߂邱�Ƃ��ł���B
�͐�Ɂi2.775�j����
�悤�Ɉ��荪��^���Ă����āA������t�Z���ċ��߂邱�Ƃ��ł���B


Next: LTR(Loop Transfer Recovery)
Up: ���o�X�g���� �iRobust Control�j
Previous: ���萫�Ɗ��x�����Ƃ̑�����
Yasunari SHIDAMA
����15�N5��12��
![]() �Ƃ���Ƃ��A
�Ƃ���Ƃ��A
![]() �A
�A
![]() �Ƃ����悤�ɁA
�Ƃ����悤�ɁA
![]() �A
�A
![]() �̍����̋��ʈ��q
�̍����̋��ʈ��q
![]() ��
���j���W�����s��i�t�s���݂���s��j�Ɍ�����Ƃ����f�Ƃ����B
��
���j���W�����s��i�t�s���݂���s��j�Ɍ�����Ƃ����f�Ƃ����B
![]() �A
�A
![]() �Ɋւ��ē��l�̏ꍇ�E�f�Ƃ����B
�Ɋւ��ē��l�̏ꍇ�E�f�Ƃ����B
![]() �̍s��
�̍s��
![]() �ɑ�������i
�ɑ�������i![]() �j�������s��
�菇�͎��̂Ƃ���ł���B
�j�������s��
�菇�͎��̂Ƃ���ł���B
![]()
![]()
![]() �Ƃ���B
�Ƃ���B
![]() ��
��
![]() ��
��![]() �s�̗v�f�̕���̍ŏ����{�������ł���B
�s�̗v�f�̕���̍ŏ����{�������ł���B
![]() ��
��![]() �s��
�s��
![]() ��
��![]() �s��
�s��![]() ���|�������̂ł���B
���|�������̂ł���B
![]() �s��
�s��
![]() ����{��ϊ��ɂ�ĉ��O�p�s��
�A���Ȃ킿
����{��ϊ��ɂ�ĉ��O�p�s��
�A���Ȃ킿
![]() �ɕϊ�����B
���̂Ƃ�
�ɕϊ�����B
���̂Ƃ�
![]() ��
��![]() �̍s��ł���A
�̍s��ł���A
![]() ��
��
![]() �̍����ʈ��q�i
�̍����ʈ��q�i
![]() �j�ɂȂ��Ă���B
�j�ɂȂ��Ă���B
![]() �A
�A
![]() �ɍ�����C�ӂ�
���j���W�����ȍs����|�������̂������ɂȂ�B
�ɍ�����C�ӂ�
���j���W�����ȍs����|�������̂������ɂȂ�B
![]() �ɂ������{��ϊ��ɂ�艺�O�p�s��ւ̕ϊ��͎��̕��@�ŋ��߂���B
�ɂ������{��ϊ��ɂ�艺�O�p�s��ւ̕ϊ��͎��̕��@�ŋ��߂���B
![]() �@
�@
![]() �̂P�s�ڂ̕���
�̂P�s�ڂ̕���![]() ��
��![]() �Ƃ̍ŏ����{��������
�Ƃ̍ŏ����{��������![]() �ł���A
�Q�s�ڂ����l�ɂ���
�ł���A
�Q�s�ڂ����l�ɂ���![]() �䂦
�䂦
![]() �̂P�s�ڂ�
�̂P�s�ڂ�
![]() �̂P�A�P�v�f
�̂P�A�P�v�f![]() ���Q�s�ڂ�
���Q�s�ڂ�
![]() �̂Q�A�Q�v�f
�̂Q�A�Q�v�f![]() ���|����
���|����
![]() �����߂��
�����߂��
![$\left[ \begin{array}{cccc}
s^2 & 0 & s-1 & 2s\\
0 & s^2& 2s-1 & 2s
\end{array} \right]$](img1624.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j�Ɓi�S��j������..
...begin{array}{cccc}
s & 0 & s-1 & s^2\\
s & s^2& 2s-1 & 0
\end{array} \right]$](img1625.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j-�i�P��j�����...
...begin{array}{cccc}
s & 0 & -1 & 0 \\
s & s^2& s-1 & -s^2
\end{array} \right]$](img1626.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j�Ɓi�R��j������..
...begin{array}{cccc}
-1 & 0 & s & 0 \\
s-1 & s^2& s & -s^2
\end{array} \right]$](img1627.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j+3\times�i�P����..
...gin{array}{cccc}
-1 & 0 & 0 & 0 \\
s-1 & s^2& s^2 & -s^2
\end{array} \right]$](img1628.png)
![$\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�R��j-�i�Q��j�A�i�S...
...]
\smash{\mathop{
\hbox to 1cm{\rightarrowfill}}\limits^{�i�P��j\times (-1)}}$](img1629.png)
![$\left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
1-s & s^2 & 0 & 0
\end{array} \right]
= [\mbox{\boldmath$P$}(s):0]$](img1630.png) �ƂȂ�B
�ƂȂ�B
![]() ��
�t������B���̂Ƃ��A
��
�t������B���̂Ƃ��A
![]() ��
��![]() ���ł���A
���ł���A
![]() ��
��![]() �̗L����
�ł���B�}2.42���
�̗L����
�ł���B�}2.42���
![]() �����
�����
![]() �ɑ�
�������������
�ɑ�
�������������
![]() �ɑ��č�����������
�ɑ��č�����������
![]() ���s������
���s������
![]() ��
��
![]() �Ƃ̍ŏ����{����
�Ƃ̍ŏ����{����![]() �Ƃ���B
�����
�Ƃ���B
�����
![]() �Ƃ��������B�܂�
�Ƃ��������B�܂�
![]() �y��
�y��
![]() �̓p�����[�^�ϓ����Ȃ����̂Ƃ��A
���̂Ƃ�
�̓p�����[�^�ϓ����Ȃ����̂Ƃ��A
���̂Ƃ�![]() ���ϓ����Ȃ��B
���ϓ����Ȃ��B
![]() �i����������
�i����������
![]() �j��
�j��
![]() ��
��
![]() �����
�����
![]() ���ϓ����Ă�
���ϓ����Ă�
![]() �̗�_�����̎����������A���̍s��������ۂ悤�ɑI�肷��Ȃ��
�A�p�����[�^���ϓ����Ă�
�̗�_�����̎����������A���̍s��������ۂ悤�ɑI�肷��Ȃ��
�A�p�����[�^���ϓ����Ă�
![$\mbox{\boldmath$P$}(s)=
\left[ \begin{array}{cc}
1 & 0 \\
1-s & s^2
\end{array} \right]$](img1693.png)
![$\bar{\mbox{\boldmath$D$}}_p(s)=
\left[ \begin{array}{cc}
s-1 & 1 \\
-s & 0
\en...
...ldmath$D$}}_u(s)=
\left[ \begin{array}{cc}
s & 0 \\
-s & 1
\end{array} \right]$](img1705.png)
![$\bar{\mbox{\boldmath$D$}}_v(s)=
\left[ \begin{array}{cc}
s^2 & 0 \\
-s & (s+1)...
...{\mbox{\boldmath$N$}}_2(s)=
\left[ \begin{array}{c}
1 \\
0
\end{array} \right]$](img1706.png)
![]() �ɂƂ��
�ɂƂ��
![]() �̍ŏI�l��
�̍ŏI�l��![]() �ƂȂ�A
�����͐����Ȃ��B
�ƂȂ�A
�����͐����Ȃ��B
![]() �͐�Ɂi2.775�j����
�悤�Ɉ��荪��^���Ă����āA������t�Z���ċ��߂邱�Ƃ��ł���B
�͐�Ɂi2.775�j����
�悤�Ɉ��荪��^���Ă����āA������t�Z���ċ��߂邱�Ƃ��ł���B