


Next: この文書について...
Up: ロバスト制御 (Robust Control)
Previous: ロバスト定常特性と外乱除去特性
図 2.43:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-8.eps} \end{center} \end{figure}](img1726.png) |
プラントの状態方程式を
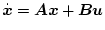 |
|
|
|
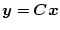 |
|
|
(2.758) |
(ただし
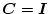 )とし、伝達関数を
)とし、伝達関数を
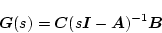 |
(2.759) |
とした場合、図2.43の還送差行列は入力端(図中の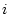 点)で見た場合
点)で見た場合
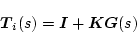 |
(2.760) |
出力端(図中の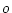 点)で見た場合
点)で見た場合
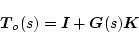 |
(2.761) |
である。もし
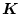 が最適フィードバック・ゲインであれば
が最適フィードバック・ゲインであれば
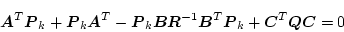 |
(2.762) |
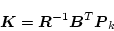 |
(2.763) |
であるから、(2.780)式を変形して
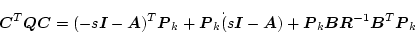 |
(2.764) |
とし、これに(2.781)、(2.777)、(2.778)式
を適用すると
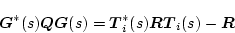 |
(2.765) |
になる。担し*印は共役転置を意味する。上式の左辺は正定であるから、
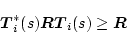 |
(2.766) |
が成立し、
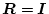 なら
なら
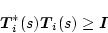 |
(2.767) |
になって、(2.642)シ式と同様低感度特性を示す。
(出力端に関しては(2.652)式で低感度性を示した)
以上
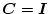 の時は、入力端、出力端とも最適制御系は低感度特性を持つ。
の時は、入力端、出力端とも最適制御系は低感度特性を持つ。
図 2.44:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-9.eps} \end{center} \end{figure}](img1740.png) |
もし
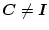 で、全状態変数が検出できないときは、カルマン・フィルタ型
またはルーエンバーガー型オブザーバが用いられる。図2.44は前者を用いた
場合である。図より
で、全状態変数が検出できないときは、カルマン・フィルタ型
またはルーエンバーガー型オブザーバが用いられる。図2.44は前者を用いた
場合である。図より
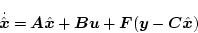 |
(2.768) |
であり、この
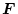 をオブザーバ・ゲインと称し、最適レギュレータの双対性から
をオブザーバ・ゲインと称し、最適レギュレータの双対性から
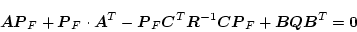 |
(2.769) |
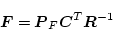 |
(2.770) |
より決定する。
この系で、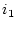 点の入力端、
点の入力端、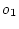 点の出力端で還送差行列を求めると(2.785)式と同様の結果が得られ低感度特性を示すが、これらは制御器内部の点であり
余り意味がない。
点の出力端で還送差行列を求めると(2.785)式と同様の結果が得られ低感度特性を示すが、これらは制御器内部の点であり
余り意味がない。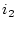 点、
点、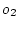 点の方が重要であるが、それらの点での還送差行列は
点の方が重要であるが、それらの点での還送差行列は
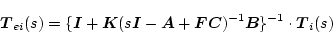 |
(2.771) |
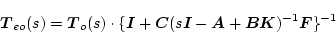 |
(2.772) |
のようになり、それぞれ
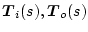 に対し付加された部分があるため、
その作用で低感度特性が保証されない。その場合の低感度特性を回復させる手法が
LTRである。
に対し付加された部分があるため、
その作用で低感度特性が保証されない。その場合の低感度特性を回復させる手法が
LTRである。
この方法は、(2.787)式の代わりに
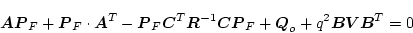 |
(2.773) |
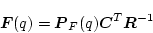 |
(2.774) |
を用い、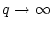 にすると最適制御の場合と等しく成り低感度特性
が回復されるという手法である。
にすると最適制御の場合と等しく成り低感度特性
が回復されるという手法である。
しかし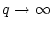 にすると
にすると
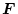 のゲインも非常に大きくなり実際的でな
くなる。そのため
のゲインも非常に大きくなり実際的でな
くなる。そのため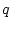 を適当な大きさに取り、有効な周波数範囲で低感度となるよ
うにする。結果的には
を適当な大きさに取り、有効な周波数範囲で低感度となるよ
うにする。結果的には
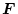 の系統のゲインを、
の系統のゲインを、
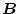 の系統のゲインより相対的に大きく
して、後者の影響を小さくする狙いであり、そのため
の系統のゲインより相対的に大きく
して、後者の影響を小さくする狙いであり、そのため
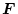 の値が大きくなるのである。
の値が大きくなるのである。
図 2.45:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-10.eps} \end{center} \end{figure}](img1756.png) |
図2.45のように出力フィードバックの系統を付加する方法である。このとき出力端の
還送差行列は
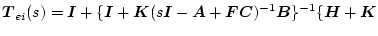 |
|
|
|
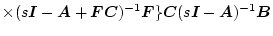 |
|
|
(2.775) |
になる。
いま右辺第2項がロバスト性をもつ
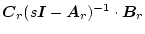 と
等しくなるように
と
等しくなるように
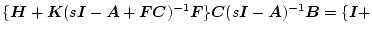 |
|
|
|
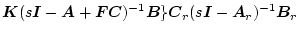 |
|
|
(2.776) |
とする。もし入出力数が等しいなら
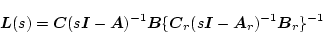 |
(2.777) |
と置くと(2.754)式は
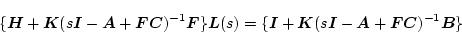 |
(2.778) |
となるので
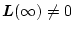 なら上式は
なら上式は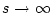 で
で
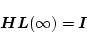 |
(2.779) |
になり、
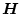 が計算できる。出力数が入力数より大きいときは類似の方法で
が計算できる。出力数が入力数より大きいときは類似の方法で
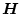 を定めることができる。
を定めることができる。
この
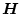 を用いるとロバスト性は得られるが、閉ループ特性が変わってくるので、
モデル追随系を用いて望ましい特性を維持させる必要がある。
を用いるとロバスト性は得られるが、閉ループ特性が変わってくるので、
モデル追随系を用いて望ましい特性を維持させる必要がある。
(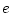 )モデルマッチングの方法
)モデルマッチングの方法
前項の方法ではモデル追随系を必要とするため次数が大きくなる。これを避けるのが
この方法である。
図 2.46:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-11.eps} \end{center} \end{figure}](img1767.png) |
図2.46に示すようにQというループが付加されている。
このときプラントの状態方程式は
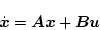 |
(2.780) |
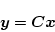 |
(2.781) |
オブザーバの状態方程式は
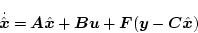 |
(2.782) |
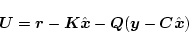 |
(2.783) |
両者をまとめて
ここで
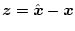 とおき
とおき
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$x$} \\
\mbox{\boldm...
...boldmath$x$} \\
\hat{\mbox{\boldmath$x$}}
\end{array} \right]
\end{displaymath}](img1776.png) |
(2.786) |
とすると
![$\displaystyle \left[ \begin{array}{c}
\dot{\mbox{\boldmath$x$}} \\
\dot{\mbox{...
...dmath$I$}
\end{array} \right]
\cdot\bar{\mbox{\boldmath$B$}}\mbox{\boldmath$r$}$](img1777.png) |
|
|
|
![$\displaystyle =
\left[ \begin{array}{cc}
\mbox{\boldmath$A$}-\mbox{\boldmath$BK...
...dmath$B$} \\
\mbox{\boldmath$0$}
\end{array} \right]
\cdot \mbox{\boldmath$r$}$](img1778.png) |
|
|
(2.787) |
![\begin{displaymath}
\mbox{\boldmath$y$}=[\mbox{\boldmath$C$},\mbox{\boldmath$0$}...
...mbox{\boldmath$x$} \\
\mbox{\boldmath$z$}
\end{array} \right]
\end{displaymath}](img1779.png) |
(2.788) |
になり、
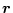 から
から
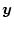 までの伝達関数は
までの伝達関数は
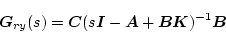 |
(2.789) |
となって、
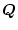 の影響はない。
の影響はない。
しかし還送差行列に関しては
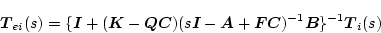 |
(2.790) |
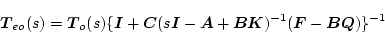 |
(2.791) |
になり、もし
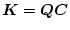 または
または
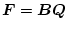 となるような
となるような
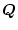 が見出せれば、
入力端または出力端でのロバスト性が得られる。
が見出せれば、
入力端または出力端でのロバスト性が得られる。
このような
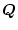 を定数で求めることは一般には困難であり(
を定数で求めることは一般には困難であり(
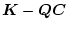 )または
(
)または
(
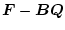 )が最小となるように選ぶ。もし
)が最小となるように選ぶ。もし
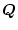 を
を
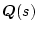 のように
のように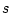 の関数とし
、入力と出力が同次数のとき
の関数とし
、入力と出力が同次数のとき
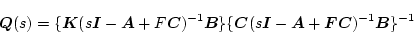 |
(2.792) |
とすると、(2.818)式で
になるから
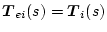 となる。
となる。
出力端の場合は
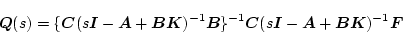 |
(2.794) |
にとれば
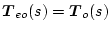 となる。
となる。
入力数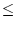 出力数のときはこの関係は求められる。ただし最小位相系でないと不安定極を
持つことになる。またこの方法は次数が増大する欠点がある。
出力数のときはこの関係は求められる。ただし最小位相系でないと不安定極を
持つことになる。またこの方法は次数が増大する欠点がある。
(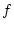 )
)
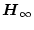 (または
(または
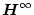 )制御
)制御
通常のユークリッド・ノルムは
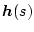 を安定で、真に(厳密)プロパな有理関数とした
とき
を安定で、真に(厳密)プロパな有理関数とした
とき
で定義される。行列の場合には
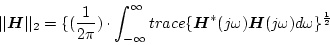 |
(2.796) |
で表示される。ここに*印は共役転置を意味する。
(2.813)式を一般的に表示すると
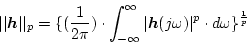 |
(2.797) |
になるが、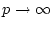 にすると
にすると
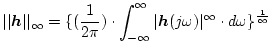 |
|
|
|
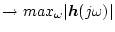 |
|
|
(2.798) |
になる。これはある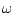 で
で
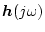 が最大になり、その所が強調される形になるからで、
ワースト・ケースを意味する。
が最大になり、その所が強調される形になるからで、
ワースト・ケースを意味する。
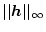 の場合は、
の場合は、
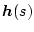 は安定でプロパな
有理関数である。
は安定でプロパな
有理関数である。
行列の場合には次式となる。
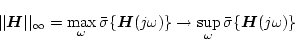 |
(2.799) |
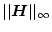 と
と
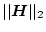 との間には
との間には
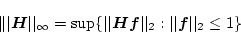 |
(2.800) |
の関係がある。
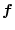 は
は
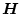 の列の数と一致する
の列の数と一致する
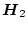 のベクトルである。
のベクトルである。
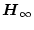 制御では制御系を次のように表示する。
制御では制御系を次のように表示する。
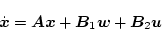 |
(2.801) |
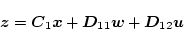 |
(2.802) |
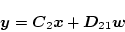 |
(2.803) |
ここで
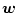 は外部入力、
は外部入力、
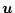 は操作入力、
は操作入力、
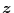 は制御量(または誤差量)、
は制御量(または誤差量)、
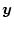 は観測出力である。
これを伝達関数で表現すると
は観測出力である。
これを伝達関数で表現すると
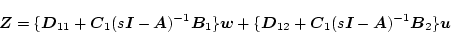 |
(2.804) |
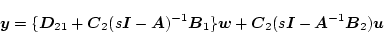 |
(2.805) |
これを一般的に書くと
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$z$} \\
\mbox{\boldm...
...mbox{\boldmath$w$} \\
\mbox{\boldmath$u$}
\end{array} \right]
\end{displaymath}](img1823.png) |
(2.806) |
ここで
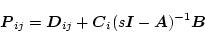 |
(2.807) |
である。制御器は
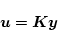 |
(2.808) |
で表され、ブロック図は図2.47の形となる。
図 2.47:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-12.eps} \end{center} \end{figure}](img1826.png) |
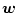 から
から
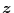 までの伝達関数は
までの伝達関数は
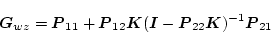 |
(2.809) |
である。なぜなら(2.824)式より
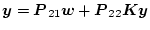
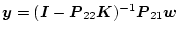
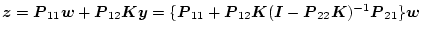 であるから。
であるから。
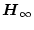 制御は閉ループ系が内部安定で、かつ
制御は閉ループ系が内部安定で、かつ
 |
(2.810) |
となるような
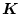 を見出すことである。
を見出すことである。
いま図2.46の場合を
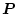 を使ってブロック図にすると図2.48
のようになる
を使ってブロック図にすると図2.48
のようになる
図 2.48:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-13.eps} \end{center} \end{figure}](img1832.png) |
図より
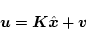 |
(2.811) |
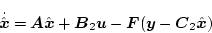 |
(2.812) |
いま
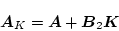 |
(2.813) |
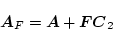 |
(2.814) |
とおき、それぞれ安定であるとする。また
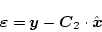 |
(2.815) |
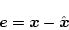 |
(2.816) |
とおく。(2.819)、(2.830)、(2.831)、
(2.834)式より
また(2.819)、(2.830)、(2.832)、(2.834)
式より
すなわち
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{\mbox{\boldmath$x$}} \\
\dot{\...
...mbox{\boldmath$w$} \\
\mbox{\boldmath$v$}
\end{array} \right]
\end{displaymath}](img1849.png) |
(2.819) |
になり、また(2.820)式は(2.830)、(2.834)
式より
また(2.833)式は(2.821)式を用い
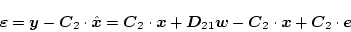 |
(2.821) |
から
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$z$} \\
\mbox{\boldm...
...mbox{\boldmath$w$} \\
\mbox{\boldmath$v$}
\end{array} \right]
\end{displaymath}](img1855.png) |
(2.822) |
(2.838)式から
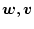 に対する
に対する
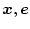 の伝達関数を求め、それを(2.841)式に代入すると
の伝達関数を求め、それを(2.841)式に代入すると
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$z$} \\
\mbox{\boldm...
...mbox{\boldmath$w$} \\
\mbox{\boldmath$v$}
\end{array} \right]
\end{displaymath}](img1855.png) |
(2.823) |
のような伝達関数行列となる。図2.49の左側のようなブロック図を考えた場合、
図 2.49:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-14.eps} \end{center} \end{figure}](img1858.png) |
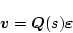 |
(2.824) |
であるから、これを(2.842)式に適用すると
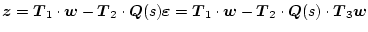 |
|
|
|
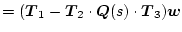 |
|
|
(2.825) |
となり同図右側の図と等価になる。
ゆえに
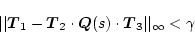 |
(2.826) |
(すなわち
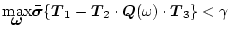 )
)
となるような
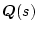 を求めるのが
を求めるのが
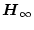 によるLTRである。
によるLTRである。
(2.812)式の前半部分
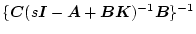 が
安定であるために
は{ }内の零点が最小位相系である必要がある。もし非最小位相系である場合は
非最小位相部分と最小位相部分とに分けて
が
安定であるために
は{ }内の零点が最小位相系である必要がある。もし非最小位相系である場合は
非最小位相部分と最小位相部分とに分けて
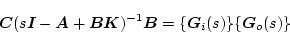 |
(2.827) |
のようにする。例えば
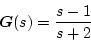 |
(2.828) |
のとき
 |
(2.829) |
のようにする。
この
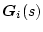 を
を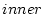 (または
(または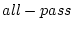 、全域通過)関数と呼び
、全域通過)関数と呼び
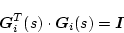 |
(2.830) |
のような性質を持つ。一方
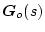 を
を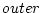 関数と呼ぶ。
関数と呼ぶ。
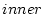 を掛けても
を掛けても
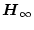 ノルムは変わらないという性質がある。
ノルムは変わらないという性質がある。
(2.812)式の
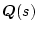 をこの
をこの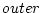 関数に関しての逆行列を取るよう
にすれば、不安定極は生じないことになるが、LTRは部分的になる。
関数に関しての逆行列を取るよう
にすれば、不安定極は生じないことになるが、LTRは部分的になる。



Next: この文書について...
Up: ロバスト制御 (Robust Control)
Previous: ロバスト定常特性と外乱除去特性
Yasunari SHIDAMA
平成15年5月12日
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-11-8.eps} \end{center} \end{figure}](img1726.png)
![]() で、全状態変数が検出できないときは、カルマン・フィルタ型
またはルーエンバーガー型オブザーバが用いられる。図2.44は前者を用いた
場合である。図より
で、全状態変数が検出できないときは、カルマン・フィルタ型
またはルーエンバーガー型オブザーバが用いられる。図2.44は前者を用いた
場合である。図より
![]() 点の入力端、
点の入力端、![]() 点の出力端で還送差行列を求めると(2.785)式と同様の結果が得られ低感度特性を示すが、これらは制御器内部の点であり
余り意味がない。
点の出力端で還送差行列を求めると(2.785)式と同様の結果が得られ低感度特性を示すが、これらは制御器内部の点であり
余り意味がない。![]() 点、
点、![]() 点の方が重要であるが、それらの点での還送差行列は
点の方が重要であるが、それらの点での還送差行列は
![]() にすると
にすると
![]() のゲインも非常に大きくなり実際的でな
くなる。そのため
のゲインも非常に大きくなり実際的でな
くなる。そのため![]() を適当な大きさに取り、有効な周波数範囲で低感度となるよ
うにする。結果的には
を適当な大きさに取り、有効な周波数範囲で低感度となるよ
うにする。結果的には
![]() の系統のゲインを、
の系統のゲインを、
![]() の系統のゲインより相対的に大きく
して、後者の影響を小さくする狙いであり、そのため
の系統のゲインより相対的に大きく
して、後者の影響を小さくする狙いであり、そのため
![]() の値が大きくなるのである。
の値が大きくなるのである。
![]() と
等しくなるように
と
等しくなるように
![]() を用いるとロバスト性は得られるが、閉ループ特性が変わってくるので、
モデル追随系を用いて望ましい特性を維持させる必要がある。
を用いるとロバスト性は得られるが、閉ループ特性が変わってくるので、
モデル追随系を用いて望ましい特性を維持させる必要がある。
![]() )モデルマッチングの方法
)モデルマッチングの方法
![]() を定数で求めることは一般には困難であり(
を定数で求めることは一般には困難であり(
![]() )または
(
)または
(
![]() )が最小となるように選ぶ。もし
)が最小となるように選ぶ。もし
![]() を
を
![]() のように
のように![]() の関数とし
、入力と出力が同次数のとき
の関数とし
、入力と出力が同次数のとき
![]() 出力数のときはこの関係は求められる。ただし最小位相系でないと不安定極を
持つことになる。またこの方法は次数が増大する欠点がある。
出力数のときはこの関係は求められる。ただし最小位相系でないと不安定極を
持つことになる。またこの方法は次数が増大する欠点がある。
![]() )
)
![]() (または
(または
![]() )制御
)制御
![]() を安定で、真に(厳密)プロパな有理関数とした
とき
を安定で、真に(厳密)プロパな有理関数とした
とき
![]() 制御では制御系を次のように表示する。
制御では制御系を次のように表示する。
![]() から
から
![]() までの伝達関数は
までの伝達関数は
![]() を使ってブロック図にすると図2.48
のようになる
を使ってブロック図にすると図2.48
のようになる
![]() が
安定であるために
は{ }内の零点が最小位相系である必要がある。もし非最小位相系である場合は
非最小位相部分と最小位相部分とに分けて
が
安定であるために
は{ }内の零点が最小位相系である必要がある。もし非最小位相系である場合は
非最小位相部分と最小位相部分とに分けて
![]() をこの
をこの![]() 関数に関しての逆行列を取るよう
にすれば、不安定極は生じないことになるが、LTRは部分的になる。
関数に関しての逆行列を取るよう
にすれば、不安定極は生じないことになるが、LTRは部分的になる。