• ［例1］重根のない場合
• ［例2］重根のある場合

Canonical Variable（正準形）

システムを部分分数に分解し、一次遅れ系の合成となるようにし、各一次 遅れ系に中間変数を取る方法で、ジョルダン標準系ともいう。

例えば

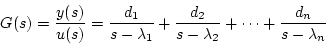$$G(s)=\frac{y(s)}{u(s)}=\frac{d_1}{s-\lambda_1}+\frac{d_2}{s-\lambda_2}+ \cdots +\frac{d_n}{s-\lambda_n}$$ (2.21)

と部分分数に分解し、状態変数を

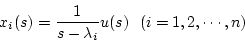$$x_i(s)=\frac{1}{s-\lambda_i}u(s) ( i=1,2,\cdots ,n )$$ (2.22)

に取る。このとき状態方程式は

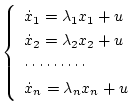$$\left\{\begin{array}{l} \dot{x}_1=\lambda_1x_1+u\\ \dot{x}_2=\lambda_2x_2+u\\ \cdots\cdots\cdots\\ \dot{x}_n=\lambda_nx_n+u \end{array}\right.$$ (2.23)

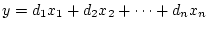$$y=d_1x_1+d_2x_2+\cdots +d_nx_n$$ (2.24)

で表される。

［例1］重根のない場合

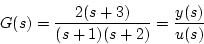$$G(s)=\frac{2(s+3)}{(s+1)(s+2)}=\frac{y(s)}{u(s)}$$ (2.25)

の場合、部分分数に分解し

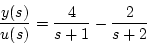$$\frac{y(s)}{u(s)}=\frac{4}{s+1}-\frac{2}{s+2}\\$$ (2.26)

$$x_1(s)=\frac{1}{s+1}u(s)$$ (2.27)

$$x_2(s)=\frac{1}{s+2}u(s)$$ (2.28)

$$y(s)=4x_1(s)-2x_2(s)$$ (2.29)

以上により状態方程式は

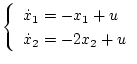$$\left\{\begin{array}{l} \dot{x}_1=-x_1+u\\ \dot{x}_2=-2x_2+u \end{array}\right.$$ (2.30)

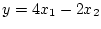$$y=4x_1-2x_2$$ (2.31)

となる。

［例2］重根のある場合

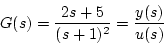$$G(s)=\frac{2s+5}{(s+1)^2}=\frac{y(s)}{u(s)}$$ (2.32)

の場合、部分分数に分解し

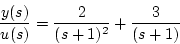$$\frac{y(s)}{u(s)}=\frac{2}{(s+1)^2}+\frac{3}{(s+1)}$$ (2.33)

として、状態変数を

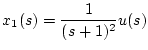$$x_1(s)=\frac{1}{(s+1)^2}u(s)$$ (2.34)

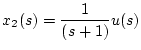$$x_2(s)=\frac{1}{(s+1)}u(s)$$ (2.35)

にとる。（2.34）式に（2.35）式を代入すると、

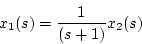$$x_1(s)=\frac{1}{(s+1)}x_2(s)$$ (2.36)

になる。したがって状態方程式は

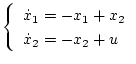$$\left\{\begin{array}{l} \dot{x}_1=-x_1+x_2\\ \dot{x}_2=-x_2+u \end{array}\right.$$ (2.37)

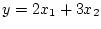$$y=2x_1+3x_2$$ (2.38)

となる。