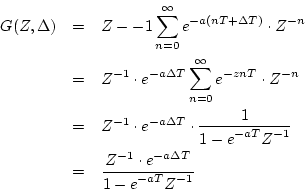

Next: 逆変換
Up: 拡張変換
Previous: 拡張変換
今迄取り扱ってきた 変換はサンプリング時刻だけを表したものである。した
がってむだ時間のようにサンプリング時刻の間に現象の変化を生じる場合には適
しない。これを考慮したのが拡張
変換はサンプリング時刻だけを表したものである。した
がってむだ時間のようにサンプリング時刻の間に現象の変化を生じる場合には適
しない。これを考慮したのが拡張 変換である。
変換である。
図 3.16:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-5-1.eps} \end{center} \end{figure}](img250.png) |
たとえば、図3.16に示すごとくむだ時間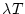 がある場合、
がある場合、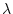 のすぐ上の整数を
のすぐ上の整数を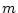 とし、
とし、
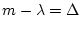 とおくと、次式のようになる。ただし、
とおくと、次式のようになる。ただし、
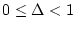 。
。
![\begin{displaymath}
{\cal L}[x(t-\lambda T)]=X(s)e^{-\lambda Ts}
=e^{-mTs}X(s)e^{\Delta Ts}
\end{displaymath}](img256.png) |
(3.47) |
これを 変換すると、
変換すると、
![\begin{displaymath}
X(Z,\Delta)=Z^{-m}Z[X(s)e^{\Delta Ts}]
=Z^{-m}\displaystyle \sum_{n=0}^{\infty}
x(nT+\Delta T)\cdot Z^{-n}
\end{displaymath}](img257.png) |
(3.48) |
となり、これが拡張 変換の式である。この式の計算は3.2(2)項で示
したのと同じような方法で行う。この拡張
変換の式である。この式の計算は3.2(2)項で示
したのと同じような方法で行う。この拡張 変換で表示された値は
変換で表示された値は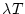 時点を基準点とし、それから以降各
時点を基準点とし、それから以降各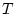 秒ごとの値を示したものである。丁度
図3.17に示すごとく
秒ごとの値を示したものである。丁度
図3.17に示すごとく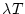 だけの遅延回路を通した後にサンプ
リングしたのに相当する。
だけの遅延回路を通した後にサンプ
リングしたのに相当する。
図 3.17:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-5-2.eps} \end{center} \end{figure}](img258.png) |
また
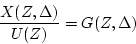 |
(3.49) |
を拡張パルス伝達関数という。
[例]
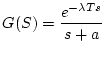 の場合の拡張
の場合の拡張 変換を求める。
変換を求める。
ただし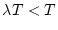 の場合。
の場合。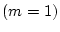
Yasunari SHIDAMA
平成15年6月9日
![]() がある場合、
がある場合、![]() のすぐ上の整数を
のすぐ上の整数を![]() とし、
とし、
![]() とおくと、次式のようになる。ただし、
とおくと、次式のようになる。ただし、
![]() 。
。
![\begin{displaymath}
X(Z,\Delta)=Z^{-m}Z[X(s)e^{\Delta Ts}]
=Z^{-m}\displaystyle \sum_{n=0}^{\infty}
x(nT+\Delta T)\cdot Z^{-n}
\end{displaymath}](img257.png)
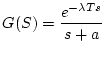 の場合の拡張
の場合の拡張![]() 変換を求める。
変換を求める。
![]() の場合。
の場合。![]()