

Next: 高周波に対する安定の確認
Up: 安定判別
Previous: 拡張したRouth-Hurwitzの安定判別法
(3.55)式の特性方程式に
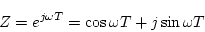 |
(3.65) |
を代入し、周波数領域とした場合
![\begin{displaymath}
1+[GH]^{*}(\omega)=0
\end{displaymath}](img324.png) |
(3.66) |
となる。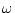 を
を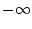 から
から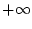 迄変えると、図3.19 (a)
の
迄変えると、図3.19 (a)
の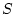 面で虚軸上をたどることになり、これは同図(b) の
面で虚軸上をたどることになり、これは同図(b) の 面では単位円上をた
どることに該当する。ただし
面では単位円上をた
どることに該当する。ただし
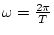 ごとに単位円上を一周す
る。
ごとに単位円上を一周す
る。 面の単位円外から
面の単位円外から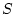 面の右半平面に相当する。したがってこの中に特性
根が存在しなければ安定である。
面の右半平面に相当する。したがってこの中に特性
根が存在しなければ安定である。
![\begin{displaymath}[GH]^{*}(\omega)=-1
\end{displaymath}](img327.png) |
(3.67) |
であるから、パルス一巡伝達関数のベクトル軌跡を描いたとき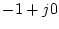 の点を不
安定領域の中に囲まれなければ安定であるといえる。
の点を不
安定領域の中に囲まれなければ安定であるといえる。
図 3.19:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-6-2.eps} \end{center} \end{figure}](img329.png) |
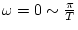 と
と
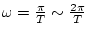 とは実軸に対して
鏡像となるので、ナイキストの安定判別法は次のごとくなる。
とは実軸に対して
鏡像となるので、ナイキストの安定判別法は次のごとくなる。
「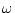 を
を
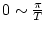 変化させたとき
パルス一巡伝達関数
変化させたとき
パルス一巡伝達関数
![$[GH]^{*}(\omega)$](img333.png) のベクトル軌跡が、
のベクトル軌跡が、
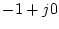 の点を左側に見れば、安定であり、右側にみれば
不安である。」
の点を左側に見れば、安定であり、右側にみれば
不安である。」
[例]図3.20の制御系の安定判別を行う。
図 3.20:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-6-3.eps} \end{center} \end{figure}](img334.png) |
パルス一巡伝達関数は
となる。上式に(3.65)式を代入すると
となる。この式の分母を実数化して、ベクトル軌跡を描いたのが
図3.21であり、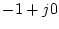 の点を左側に
見るので安定である。
の点を左側に
見るので安定である。
図 3.21:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-6-4.eps} \end{center} \end{figure}](img337.png) |
なおベクトル軌跡と同様にボード線図によっても
安定判別を行うことができる。
Yasunari SHIDAMA
平成15年6月9日
![]() と
と
![]() とは実軸に対して
鏡像となるので、ナイキストの安定判別法は次のごとくなる。
とは実軸に対して
鏡像となるので、ナイキストの安定判別法は次のごとくなる。
![]() を
を
![]() 変化させたとき
パルス一巡伝達関数
変化させたとき
パルス一巡伝達関数
![]() のベクトル軌跡が、
のベクトル軌跡が、
![]() の点を左側に見れば、安定であり、右側にみれば
不安である。」
の点を左側に見れば、安定であり、右側にみれば
不安である。」
![\begin{eqnarray*}[GH]^{*}(\omega)
& = & \frac{\displaystyle 0.368
(\cos \omega ...
... T+0.368)
+j(2\cos \omega T\sin \omega T
-1.368\sin \omega T)}
\end{eqnarray*}](img336.png)