

Next: サンプリングによる側帯波のうち重要成分のみを考慮する方法
Up: サンプリング制御系の設計
Previous: 概要
連続信号としての補償を行う場合、ホールド回路が
零次ホールドであれば
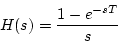 |
(3.72) |
で表されるから、周波数伝達関数は
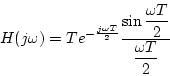 |
(3.73) |
と書き直される。
いま制御対象の伝達関数が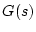 のとき、ホールド回路と制御対象と
結合したパルス周波数伝達関数は(3.9)式より
のとき、ホールド回路と制御対象と
結合したパルス周波数伝達関数は(3.9)式より
となる。通常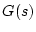 は低周波ろ波特性を有しているので、
は低周波ろ波特性を有しているので、
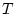 が十分小さいときは
が十分小さいときは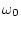 成分は無視できる。
したがって、上式は近似的に
成分は無視できる。
したがって、上式は近似的に
![\begin{displaymath}[HG]^{*}(j\omega) =\hspace{-1em}\raisebox{1.1ex}{.}\hspace{.1...
...c{\displaystyle \omega T}{\displaystyle 2}}
\cdot
G(j\omega)
\end{displaymath}](img366.png) |
(3.75) |
となり、更に
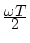 の小さい所では
の小さい所では
![\begin{displaymath}[HG]^{*}(j\omega)=\hspace{-1em}\raisebox{1.1ex}{.}\hspace{.1e...
...ex}{.}\hspace{.3em}e^{-j\frac{\omega T}{2}}
\cdot
G(j\omega)
\end{displaymath}](img368.png) |
(3.76) |
として扱うことができる。すなわち、図3.24(a)のブロック
ダイヤグラムは図3.25のような連続系と等価
として扱うことができ、これは図3.26の
点線で示すものに近似して扱うことを意味している。
図 3.25:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-2.eps} \end{center} \end{figure}](img369.png) |
図 3.26:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-3.eps} \end{center} \end{figure}](img370.png) |
したがって、次のような手順で設計を行う。
- #1.
- サンプル及びホールド動作を連続系で近似する。
- #2.
- 連続系としての系の設計を行う。
- #3.
 変換解析法で、設計された系の正確な解析を行い、必要があ
れば設計を繰り返す。
変換解析法で、設計された系の正確な解析を行い、必要があ
れば設計を繰り返す。
[例]
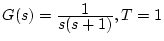 の場合の設計を行う。
連続系で近似すると、
の場合の設計を行う。
連続系で近似すると、
となる。このボード線図を描くと図3.27(a)
となり、位相余裕は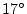 しかない。そこで、
しかない。そこで、
の補償要素を加えると、図3.27(b)
となり位相余裕は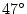 に改善される。
に改善される。
図 3.27:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-4.eps} \end{center} \end{figure}](img376.png) |


Next: サンプリングによる側帯波のうち重要成分のみを考慮する方法
Up: サンプリング制御系の設計
Previous: 概要
Yasunari SHIDAMA
平成15年6月9日
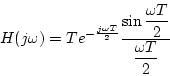
![]() のとき、ホールド回路と制御対象と
結合したパルス周波数伝達関数は(3.9)式より
のとき、ホールド回路と制御対象と
結合したパルス周波数伝達関数は(3.9)式より
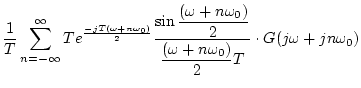
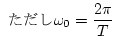
![\begin{displaymath}[HG]^{*}(j\omega) =\hspace{-1em}\raisebox{1.1ex}{.}\hspace{.1...
...c{\displaystyle \omega T}{\displaystyle 2}}
\cdot
G(j\omega)
\end{displaymath}](img366.png)