

Next: 変換
Up: サンプル値の表現と変換
Previous: サンプル値の表現と変換
サンプラは図3.2に示すごとく連続的入出力波形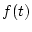 を周期
を周期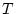 で
サンプリングして出力波形としてパルス列
で
サンプリングして出力波形としてパルス列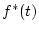 を出す。
を出す。
図 3.2:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-1.eps} \end{center} \end{figure}](img8.png) |
サンプリングされた個々のパルス信号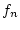 を
を
で表すと、パルス列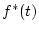 は次式で表される。
は次式で表される。
いま、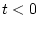 では
では 、
、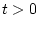 では
では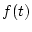 なる連続関数をサンプリングした場合
なる連続関数をサンプリングした場合
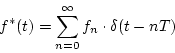 |
(3.3) |
となる。これをラプラス変換すると
![\begin{displaymath}
{\cal L}\left[f^{*}(t)\right]=F^{*}(s)=
\sum_{n=0}^{\infty}f_{n}\cdot e^{-nst}
\end{displaymath}](img23.png) |
(3.4) |
となる。この式により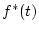 が
が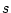 領域で表されたことになる。
領域で表されたことになる。
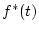 のラプラス変換にはもう一つの形がある。すなわち
のラプラス変換にはもう一つの形がある。すなわち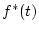 を図3.3のごとく連続信号
を図3.3のごとく連続信号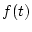 をパルス列
をパルス列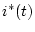 で変調したもの
として考える。このパルス列
で変調したもの
として考える。このパルス列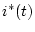 は図3.4のごとき方形波
は図3.4のごとき方形波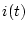 において、
において、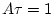 で
で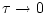 の極限値の場合とする。
の極限値の場合とする。
図 3.3:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-2.eps} \end{center}\end{figure}](img28.png) |
図 3.4:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-3.eps} \end{center}\end{figure}](img29.png) |
一般に周期関数は次のフーリエ級数で表示することができる。
これに図3.4の波形を適用すると
となる。そして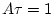 とし、
とし、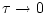 の極限値を求めると、上式の
第2項は
の極限値を求めると、上式の
第2項は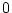 となり、第3項の
となり、第3項の
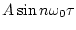 は
は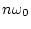 となる。
となる。
したがって
となる。
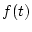 を
を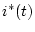 で変調した信号
で変調した信号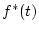 は
は
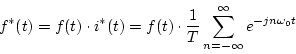 |
(3.8) |
となり、上式をラプラス変換すると
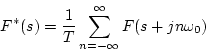 |
(3.9) |
となる。これが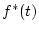 のラプラス変換のもう一つの形である。
のラプラス変換のもう一つの形である。
上式で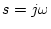 とおくと
とおくと
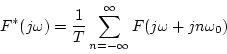 |
(3.10) |
となる。この式から次のことがいえる。
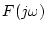 の周波数特性
の周波数特性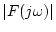 の図が図3.5のごとく
の図が図3.5のごとく
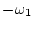 から
から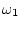 までであとは
までであとは であったとすると、
であったとすると、
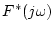 の周波数特性
の周波数特性
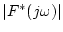 は
(3.10)式より図3.6のようになる。この図の場合は
は
(3.10)式より図3.6のようになる。この図の場合は
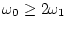 の場合であり、このときは、
の場合であり、このときは、
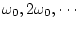 を中心とする周波数特性は重なり合わない。
したがって、
を中心とする周波数特性は重なり合わない。
したがって、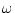 が
が
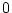 から
から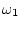 までの間だけ通過する理想的な
ろ波器を通過させることによりもとの
までの間だけ通過する理想的な
ろ波器を通過させることによりもとの
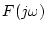 の周波数特性にすることができる。このことから次の
シャノンのサンプリング定理が云われている。
の周波数特性にすることができる。このことから次の
シャノンのサンプリング定理が云われている。
「最高の周波数として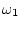 ま、での周波数成分を含む信号をサンプルし、
ついでこのサンプル値からフィルタを通してもとの信号を取り出しうるためには、
サンプリング周波数
ま、での周波数成分を含む信号をサンプルし、
ついでこのサンプル値からフィルタを通してもとの信号を取り出しうるためには、
サンプリング周波数
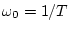 が
が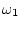 の少なくとも2倍、すなわち
の少なくとも2倍、すなわち
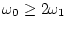 でなければならない。」
でなければならない。」
実際には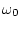 としては
としては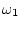 の10倍あるいはそれ以上のものを
用いるのが普通である。
の10倍あるいはそれ以上のものを
用いるのが普通である。
図 3.5:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-4.eps} \end{center} \end{figure}](img58.png) |
図 3.6:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-5.eps} \end{center} \end{figure}](img59.png) |


Next: 変換
Up: サンプル値の表現と変換
Previous: サンプル値の表現と変換
Yasunari SHIDAMA
平成15年6月9日
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-1.eps} \end{center} \end{figure}](img8.png)
![]() を
を
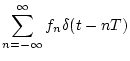
![]() では
では![]() 、
、![]() では
では![]() なる連続関数をサンプリングした場合
なる連続関数をサンプリングした場合
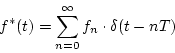
![]() のラプラス変換にはもう一つの形がある。すなわち
のラプラス変換にはもう一つの形がある。すなわち![]() を図3.3のごとく連続信号
を図3.3のごとく連続信号![]() をパルス列
をパルス列![]() で変調したもの
として考える。このパルス列
で変調したもの
として考える。このパルス列![]() は図3.4のごとき方形波
は図3.4のごとき方形波![]() において、
において、![]() で
で![]() の極限値の場合とする。
の極限値の場合とする。
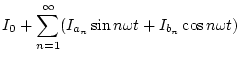
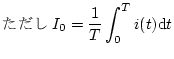
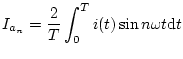
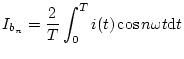
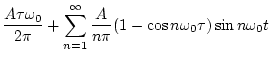
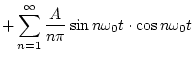
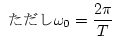
![$\displaystyle \frac{\omega_{0}}{2\pi}
\left[1+\sum_{n=1}^{\infty}
(e^{jn\omega_{0} t} + e^{-jn\omega_{0} t})\right]$](img41.png)
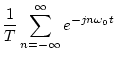
![]() を
を![]() で変調した信号
で変調した信号![]() は
は
![]() とおくと
とおくと
![]() ま、での周波数成分を含む信号をサンプルし、
ついでこのサンプル値からフィルタを通してもとの信号を取り出しうるためには、
サンプリング周波数
ま、での周波数成分を含む信号をサンプルし、
ついでこのサンプル値からフィルタを通してもとの信号を取り出しうるためには、
サンプリング周波数
![]() が
が![]() の少なくとも2倍、すなわち
の少なくとも2倍、すなわち
![]() でなければならない。」
でなければならない。」
![]() としては
としては![]() の10倍あるいはそれ以上のものを
用いるのが普通である。
の10倍あるいはそれ以上のものを
用いるのが普通である。