

Next: 状態観測器(State Obserber)
Up: 離散値系制御理論
Previous: 極配置制御(Pole assignment)
最適制御理論
離散値系の最適制御のおける評価関数は、二乗形の場合、次式のような形にとる。
![\begin{displaymath}
J=\sum_{k=0}^{N-1} \left[ \frac{1}{2}\mbox{\boldmath$x$}^T(k...
...c{1}{2}\mbox{\boldmath$u$}^T(k)\mbox{\boldmath$Ru$}(k) \right]
\end{displaymath}](img606.png) |
(4.287) |
ここで、
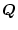 は
は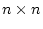 の準正定対称マトリクス、
の準正定対称マトリクス、
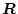 は
は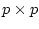 の
正定対称マトリクスとする。これらはウェイトを示している。
の
正定対称マトリクスとする。これらはウェイトを示している。
いまシステム方程式を次式とする。
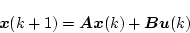 |
(4.288) |
このときLagrangeの未定定数を
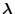 とすると、補助関数は
とすると、補助関数は
で表される。この補助関数を
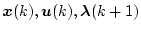 で偏微分し
て、0としたとき(4.289)式の拘束条件のもとで、(4.288)式
を最小にする条件が得られる。すなわち
で偏微分し
て、0としたとき(4.289)式の拘束条件のもとで、(4.288)式
を最小にする条件が得られる。すなわち
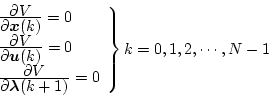 |
(4.290) |
である。
![\begin{displaymath}
\frac{\partial}{\partial\mbox{\boldmath$x$}(k)}
\left[ \frac...
...}^T(k)\mbox{\boldmath$Qx$}(k) \right] =\mbox{\boldmath$Qx$}(k)
\end{displaymath}](img615.png) |
(4.291) |
![\begin{displaymath}
\frac{\partial}{\partial\mbox{\boldmath$x$}(k)}
\left[ \mbox...
...) \right] =\mbox{\boldmath$A$}^T\mbox{\boldmath$\lambda$}(k+1)
\end{displaymath}](img616.png) |
(4.292) |
ゆえ
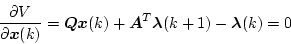 |
(4.293) |
となる。同様にして
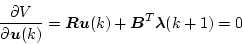 |
(4.294) |
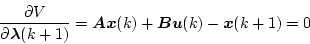 |
(4.295) |
が得られる。(4.294)式より
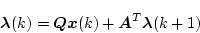 |
(4.296) |
(4.295)式より
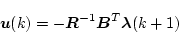 |
(4.297) |
(4.296)式に(4.298)式を代入すると
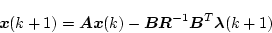 |
(4.298) |
となる。いま
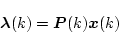 |
(4.299) |
とおく。この
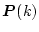 は
は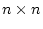 の正定対称な行列とする。
(4.297)式に適用すると
の正定対称な行列とする。
(4.297)式に適用すると
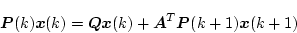 |
(4.300) |
となる。また(4.299)式は
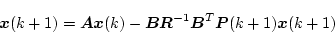 |
(4.301) |
となり
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1)=[\mbox{\boldmath$I$}+\mbox{\boldmat...
...ath$B$}^T\mbox{\boldmath$P$}(k+1)]^{-1}\mbox{\boldmath$Ax$}(k)
\end{displaymath}](img627.png) |
(4.302) |
が得られる。これを(4.301)式に代入すると、
となる。上式より次式が得られる。
![\begin{displaymath}
\mbox{\boldmath$P$}(k)=\mbox{\boldmath$Q$}+\mbox{\boldmath$A...
...ldmath$B$}^T
\mbox{\boldmath$P$}(k+1)]^{-1}\mbox{\boldmath$A$}
\end{displaymath}](img631.png) |
(4.304) |
この式はリカッチ方程式に相当し、
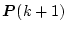 から
から
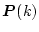 が定まる逆時間
の式である。
が定まる逆時間
の式である。
いま補助関数を
 で偏微分すると
で偏微分すると
 の項以外は0となり
の項以外は0となり
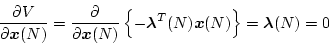 |
(4.305) |
となる。これを(4.300)式に代入すると
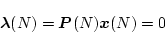 |
(4.306) |
となり、もし
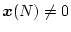 なら
なら
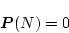 |
(4.307) |
となる。この条件を(4.305)式に適用すれば逆時間的に、各
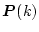 が求められる。
が求められる。
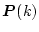 が求められると、(4.297)、(4.298)、
(4.300)式より
が求められると、(4.297)、(4.298)、
(4.300)式より
の関係が得られるので、最適制御法則
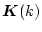 が得られる。次例で示すようにこの
が得られる。次例で示すようにこの
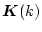 は
は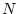 を大きくとると
を大きくとると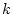 の小さい間は一定値をとるので定数として
扱うことができる。
の小さい間は一定値をとるので定数として
扱うことができる。
[例]システム方程式が次式のとき
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...eft[ \begin{array}{c}
1.0 \\
0.5
\end{array} \right] u(k)
\end{displaymath}](img645.png) |
(4.309) |
評価関数
![\begin{displaymath}
J=\sum_{k=0}^{N-1} \left[ \frac{1}{2} \{ x_1^2(k)+x_2^2(k) \}
+\frac{1}{2}u^2(k) \right]
\end{displaymath}](img646.png) |
(4.310) |
を最小にする最適制御法則を求める。また初期条件を
としたときの応答を求める。
上例では
である。
いま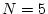 とした場合、
とした場合、
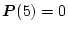 ゆえ、(4.305)式に代入すると
ゆえ、(4.305)式に代入すると
となる。そこで(4.309)式から
となる。次に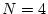 の所では
の所では
となるから
ゆえに
となる。この計算を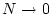 まで続けると、各時点のフィードバックゲイン
まで続けると、各時点のフィードバックゲイン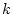 が
定まる。この結果が表4.1である。
が
定まる。この結果が表4.1である。
表 4.1:
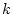 |
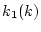 |
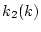 |
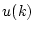 |
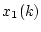 |
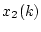 |
| 0 |
-0.395 |
-0.687 |
-39.5 |
100 |
0 |
| 1 |
-0.395 |
-0.687 |
-2.43 |
40.5 |
-19.75 |
| 2 |
-0.395 |
-0.677 |
3.48 |
10.22 |
-11.09 |
| 3 |
-0.355 |
-0.555 |
1.42 |
0.54 |
-3.8 |
| 4 |
0 |
0 |
0 |
-1.45 |
-9.42 |
この結果より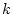 の小さい所では
の小さい所では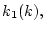
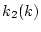 は一定値であることがわか
る。これが最適制御法則である。次に
は一定値であることがわか
る。これが最適制御法則である。次に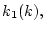
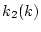 が求まれば
(4.309)式より
が求まれば
(4.309)式より
が求まり、これを(4.289)式に代入して
が求まる。これを繰り返して
という具合に
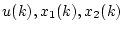 の応答が順次求められる。この結果も表
4.1に示してある。
の応答が順次求められる。この結果も表
4.1に示してある。
図4.22は と
と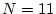 にとった場合の
にとった場合の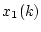 と
と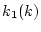 を描いた
ものである。
を描いた
ものである。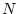 を大きくすれば
を大きくすれば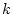 のより大きな範囲で
のより大きな範囲で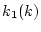 が一定値となり、
が一定値となり、
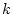 が定数として扱えることがわかる。
が定数として扱えることがわかる。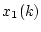 の方は、
の方は、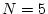 の場合でも
の場合でも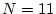 の場合でも同じ応答をすることを示している。
の場合でも同じ応答をすることを示している。
図 4.22:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-7-1.eps} \end{center} \end{figure}](img676.png) |


Next: 状態観測器(State Obserber)
Up: 離散値系制御理論
Previous: 極配置制御(Pole assignment)
Yasunari SHIDAMA
平成15年6月30日
![\begin{displaymath}
J=\sum_{k=0}^{N-1} \left[ \frac{1}{2}\mbox{\boldmath$x$}^T(k...
...c{1}{2}\mbox{\boldmath$u$}^T(k)\mbox{\boldmath$Ru$}(k) \right]
\end{displaymath}](img606.png)
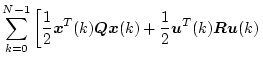
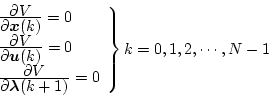
![]() で偏微分すると
で偏微分すると
![]() の項以外は0となり
の項以外は0となり
![]() が求められると、(4.297)、(4.298)、
(4.300)式より
が求められると、(4.297)、(4.298)、
(4.300)式より
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...eft[ \begin{array}{c}
1.0 \\
0.5
\end{array} \right] u(k)
\end{displaymath}](img645.png)
![\begin{displaymath}
J=\sum_{k=0}^{N-1} \left[ \frac{1}{2} \{ x_1^2(k)+x_2^2(k) \}
+\frac{1}{2}u^2(k) \right]
\end{displaymath}](img646.png)
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \r...
...=
\left[ \begin{array}{c}
100.0 \\
0
\end{array} \right]
\end{displaymath}](img647.png)
![\begin{displaymath}
\mbox{\boldmath$Q$} = \left[ \begin{array}{cc}
1 & 0 \\
...
...} = \left[ \begin{array}{c}
1.0 \\
0.5
\end{array} \right]
\end{displaymath}](img648.png)
![]() とした場合、
とした場合、
![]() ゆえ、(4.305)式に代入すると
ゆえ、(4.305)式に代入すると
![$\displaystyle \mbox{\boldmath$Q$} = \left[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]$](img653.png)
![$\displaystyle \left[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right] +
\left[ \begin{array}{cc}
0.355 & 0.355 \\
0.355 & 0.555
\end{array} \right]$](img658.png)
![$\displaystyle - \left[ \begin{array}{cc}
0 & 1
\end{array} \right]
\left[ \begi...
...{cc}
0.355 & 0.355 \\
0.355 & 0.555
\end{array} \right] \mbox{\boldmath$x$}(3)$](img661.png)
![$\displaystyle - \left[ \begin{array}{cc}
0.355 & 0.555
\end{array} \right]
\left[ \begin{array}{c}
x_1(3) \\
x_2(3)
\end{array} \right]$](img662.png)
![]() の小さい所では
の小さい所では![]()
![]() は一定値であることがわか
る。これが最適制御法則である。次に
は一定値であることがわか
る。これが最適制御法則である。次に![]()
![]() が求まれば
(4.309)式より
が求まれば
(4.309)式より
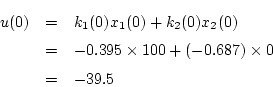
![\begin{eqnarray*}
\mbox{\boldmath$x$}(1) &=& \mbox{\boldmath$Ax$}(0)+\mbox{\bold...
...& \left[ \begin{array}{c}
40.5 \\
-19.75
\end{array} \right]
\end{eqnarray*}](img672.png)
![\begin{eqnarray*}
u(1) &=& (-0.395\times 40.5)+(-0.687)\times (-19.75) \\
&=& ...
... \left[ \begin{array}{c}
10.22 \\
-11.09
\end{array} \right]
\end{eqnarray*}](img673.png)
![]() と
と![]() にとった場合の
にとった場合の![]() と
と![]() を描いた
ものである。
を描いた
ものである。![]() を大きくすれば
を大きくすれば![]() のより大きな範囲で
のより大きな範囲で![]() が一定値となり、
が一定値となり、
![]() が定数として扱えることがわかる。
が定数として扱えることがわかる。![]() の方は、
の方は、![]() の場合でも
の場合でも![]() の場合でも同じ応答をすることを示している。
の場合でも同じ応答をすることを示している。