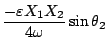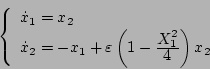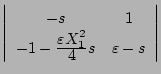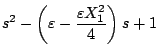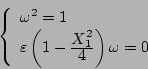

Next: 断片的線形化法
Up: 記述関数法(Describing Function)
Previous: 閉回路周波数応答
図5.17で示すような非線形要素を含む閉ループ系の状態方程式は
次式で表される。
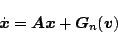 |
(5.48) |
いまここでは
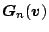 を非線形奇関数で、
を非線形奇関数で、
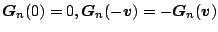 であるとする。入力
であるとする。入力
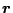 が0のときは
が0のときは
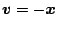 となる。
となる。
この系に振動が発生している場合を考える。前述のように、
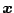 が
近似的に正弦波状と見なされると、非線形要素への入力
が
近似的に正弦波状と見なされると、非線形要素への入力
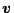 も正弦波状と
考えられるから、その各成分は次式で表される。
も正弦波状と
考えられるから、その各成分は次式で表される。
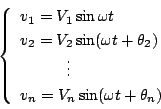 |
(5.49) |
この式は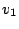 を位相の基準にとってあることを意味している。このような
を位相の基準にとってあることを意味している。このような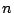 個
の正弦波が非線形要素に加わった場合、非線形要素の各出力の波形は一般に歪ん
だ形をしており次式の左辺で表されるが、高調波成分を省略し、基本波成分のみ
で近似すると次式の右辺で表すことができる。
個
の正弦波が非線形要素に加わった場合、非線形要素の各出力の波形は一般に歪ん
だ形をしており次式の左辺で表されるが、高調波成分を省略し、基本波成分のみ
で近似すると次式の右辺で表すことができる。
ただし、
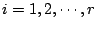 であり、
であり、
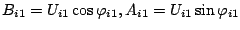 である。この
である。この はフーリエ級数の公式から
はフーリエ級数の公式から
によって決定される。これは前述した記述関数の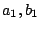 ((5.20)
式)に相当する。
((5.20)
式)に相当する。
非線形要素の出力が(5.50)式で表されると、右辺の第1項は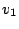 、
すな、わち
、
すな、わち
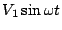 と同位相であり、第2項は
と同位相であり、第2項は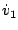 すなわち
すなわち
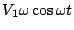 と同位相であることがわかる。
と同位相であることがわかる。
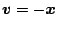 ゆえ、第1項は
ゆえ、第1項は
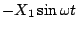 と、第2項は
と、第2項は
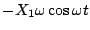 と同位相であるともいえ、これを
(5.50)式に適用すると
と同位相であるともいえ、これを
(5.50)式に適用すると
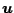 は
は
![\begin{displaymath}
\mbox{\boldmath$u$} = \mbox{\boldmath$G$}_n(\mbox{\boldmath$...
... A_{21} \\
\vdots \\
A_{n1}
\end{array} \right] \dot{x}_1
\end{displaymath}](img189.png) |
(5.51) |
と書くことができる。したがってこれを(5.48)式に適用すると
となる。いま
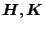 なる二つの
なる二つの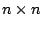 行列を導入し、
その第1列の要素をそれぞれ
行列を導入し、
その第1列の要素をそれぞれ
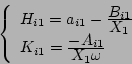 |
(5.53) |
その他の列の要素を
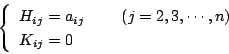 |
(5.54) |
(ただし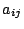 は
は
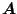 の各要素)とすると(5.53)式は
の各要素)とすると(5.53)式は
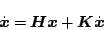 |
(5.55) |
で表される。この式は近似線形化された式であるので、この式をラプラス変換し
特性方程式を求めると
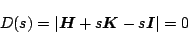 |
(5.56) |
となる。この式より安定判別を行うのであるが、
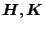 の値が振幅に依
存するので、上式に
の値が振幅に依
存するので、上式に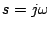 を代入し、実数成分と虚数成分の各々に対して
成立する二式を連立させ、それより安定性あるいはリミットサイクルの判定を行
う。
を代入し、実数成分と虚数成分の各々に対して
成立する二式を連立させ、それより安定性あるいはリミットサイクルの判定を行
う。
[例1]バックラッシュのあるサーボ系
(5.33)図に示すようなバックラッシュのあるサーボ系の
状態方程式は次式で表される。
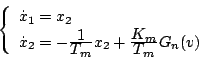 |
(5.57) |
この非線形部分に(5.54)式を適用し、(5.56)式の形にすると
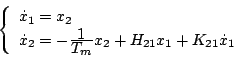 |
(5.58) |
となる。この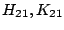 は(5.34)式、(5.35)式より
は(5.34)式、(5.35)式より
となる。
一方(5.59)式より、
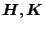 はそれぞれ
はそれぞれ
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$H$} = \left[ \begin{arr...
...y}{cc}
0 & 0 \\
K_{21} & 0
\end{array} \right]
\end{array}\end{displaymath}](img207.png) |
(5.59) |
となるので(5.57)式の特性方程式は
となる。これに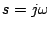 を代入し、実数部と虚数部に分けて書くと次式になる。
を代入し、実数部と虚数部に分けて書くと次式になる。
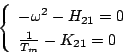 |
(5.61) |
これに(5.60)式を代入すると
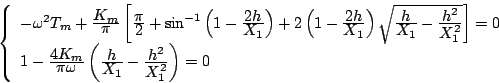 |
(5.62) |
となる。
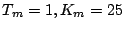 のときの両式を満足するのは
のときの両式を満足するのは
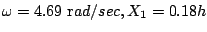 のときであり、この周波数と振幅のリミットサイクルが発生することになる。
のときであり、この周波数と振幅のリミットサイクルが発生することになる。
[例2]Van Der Polの方程式
この方程式は次式で表される
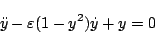 |
(5.63) |
これは非線形の微分方程式である。いま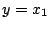 として相変数の状態方程式で
表すと次式となる。
として相変数の状態方程式で
表すと次式となる。
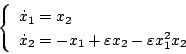 |
(5.64) |
上式より
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$A$} = \left[ \begin{arr...
...G$}_{n2}(\mbox{\boldmath$x$})
\end{array} \right]
\end{array}\end{displaymath}](img220.png) |
(5.65) |
と書ける。いま
とした場合、(5.55)式と(5.67)式より
となり、(5.51)、(5.54)、(5.67)式より
が得られる。また(5.55)式より
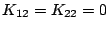 であり、(5.51)、(5.54)式より
であり、(5.51)、(5.54)式より
となる。したがって(5.56)式の形式にすると
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}} =
\left[ \begin{array}{cc}
0 & 1...
...n \theta _2 & 0
\end{array} \right] \dot{\mbox{\boldmath$x$}}
\end{displaymath}](img245.png) |
(5.70) |
となる。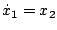 であるから、
であるから、
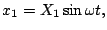
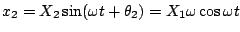 となるので
となるので
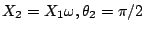 の関係が成立する。
これを(5.72)式に代入すると、
の関係が成立する。
これを(5.72)式に代入すると、
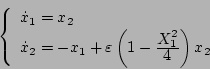 |
(5.71) |
となる。これより特性方程式は
となり、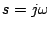 を代入すると
を代入すると
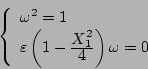 |
(5.73) |
となって、
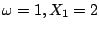 がリミットサイクルの条件となる。
がリミットサイクルの条件となる。


Next: 断片的線形化法
Up: 記述関数法(Describing Function)
Previous: 閉回路周波数応答
Yasunari SHIDAMA
平成15年7月28日
![]() が
近似的に正弦波状と見なされると、非線形要素への入力
が
近似的に正弦波状と見なされると、非線形要素への入力
![]() も正弦波状と
考えられるから、その各成分は次式で表される。
も正弦波状と
考えられるから、その各成分は次式で表される。
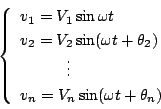
![]() 、
すな、わち
、
すな、わち
![]() と同位相であり、第2項は
と同位相であり、第2項は![]() すなわち
すなわち
![]() と同位相であることがわかる。
と同位相であることがわかる。
![]() ゆえ、第1項は
ゆえ、第1項は
![]() と、第2項は
と、第2項は
![]() と同位相であるともいえ、これを
(5.50)式に適用すると
と同位相であるともいえ、これを
(5.50)式に適用すると
![]() は
は
![\begin{displaymath}
\mbox{\boldmath$u$} = \mbox{\boldmath$G$}_n(\mbox{\boldmath$...
... A_{21} \\
\vdots \\
A_{n1}
\end{array} \right] \dot{x}_1
\end{displaymath}](img189.png)
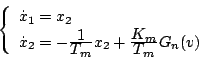
![]() はそれぞれ
はそれぞれ
![\begin{displaymath}
\begin{array}{ccc}
\mbox{\boldmath$H$} = \left[ \begin{arr...
...y}{cc}
0 & 0 \\
K_{21} & 0
\end{array} \right]
\end{array}\end{displaymath}](img207.png)
![$\displaystyle \left\vert \begin{array}{c}
\left[ \begin{array}{cc}
0 & 1 \\
H_...
...[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{array} \right\vert$](img209.png)
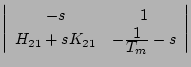
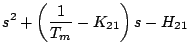
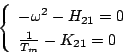
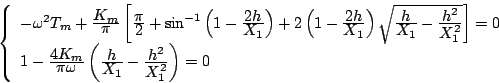
![]() のときの両式を満足するのは
のときの両式を満足するのは
![]() のときであり、この周波数と振幅のリミットサイクルが発生することになる。
のときであり、この周波数と振幅のリミットサイクルが発生することになる。
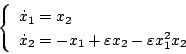
![\begin{displaymath}
\mbox{\boldmath$H$} = \left[ \begin{array}{cc}
H_{11} & H_{...
...cc}
K_{11} & K_{12} \\
K_{21} & K_{22}
\end{array} \right]
\end{displaymath}](img221.png)
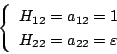
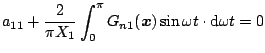
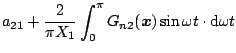
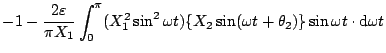
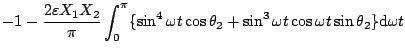
![$\displaystyle -1-\frac{2\varepsilon X_1X_2}{\pi}
\left[ \left\{ \frac{-\sin ^3\...
...{2}
-\frac{1}{4}\sin 2\omega t \right)
\right\} \cos \theta _2 \right] _0^{\pi}$](img231.png)
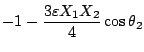
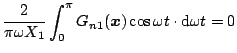
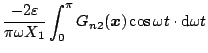
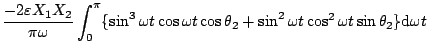
![$\displaystyle \frac{-2\varepsilon X_1X_2}{\pi \omega}
\left[ -\frac{1}{8} \left (\frac{1}{4}\sin 4\omega t-\omega t \right)
\sin \theta _2 \right] _0^{\pi}$](img243.png)