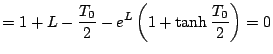

Next: 最短時間オン・オフ制御
Up: 断片的線形化法
Previous: 一次遅れ系のオン・オフ制御
単入力多次系の場合、状態方程式は
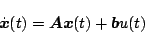 |
(5.97) |
で表され、この解は
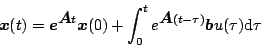 |
(5.98) |
である。
オン・オフ要素の場合
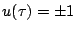 であるから
であるから
と書ける。
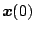 は初期値であるから、オン・オフの切換時に前区間の最
終値を次の区間の初期値として計算すればよい。
は初期値であるから、オン・オフの切換時に前区間の最
終値を次の区間の初期値として計算すればよい。
いま図5.25のような閉ループ系に発生したリミットサイクルの半周期
を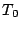 としたとき、オンの区間のみを考えると
としたとき、オンの区間のみを考えると
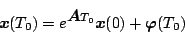 |
(5.100) |
と書ける。リミットサイクルになるのは
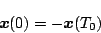 |
(5.101) |
の場合と考えられる。したがってこれを(5.102)式に適用すると
![\begin{displaymath}
\mbox{\boldmath$x$} (0) = - [\mbox{\boldmath$I$} + e^{\mbox{\boldmath$A$} T_0 } ]^{-1} \mbox{\boldmath$\varphi$} (T_0)
\end{displaymath}](img336.png) |
(5.102) |
となり、これがリミットサイクルの振幅
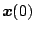 と半周期(
と半周期(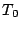 )との関係を
表している。
)との関係を
表している。
一方、オン・オフ要素への入力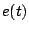 は
は
![\begin{displaymath}
e(t)= -\mbox{\boldmath$c$} ^T \mbox{\boldmath$x$} (t) = - \...
...t} \mbox{\boldmath$x$} (0) +
\mbox{\boldmath$\varphi $} (t) ]
\end{displaymath}](img339.png) |
(5.103) |
で表され、ヒステリシスのないオン・オフ要素の場合、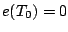 となるので
となるので
![\begin{displaymath}
- \mbox{\boldmath$c$} ^T [e^ {\mbox{\boldmath$A$} T_0} \mbox{\boldmath$x$} (0) + \mbox{\boldmath$\varphi $} (T_0) ] =0
\end{displaymath}](img341.png) |
(5.104) |
またヒステリシス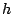 がある場合は
がある場合は
![\begin{displaymath}
- \mbox{\boldmath$c$} ^T [e^ {\mbox{\boldmath$A$} T_0} \mbox{\boldmath$x$} (0) + \mbox{\boldmath$\varphi $} (T_0) ] =-h
\end{displaymath}](img342.png) |
(5.105) |
さらに、むだ時間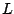 がある場合には
がある場合には
![\begin{displaymath}
-\mbox{\boldmath$c$} ^T [e^ {\mbox{\boldmath$A$}(T_0-L)} \mbox{\boldmath$x$} (0) + \mbox{\boldmath$\varphi $} (T_0-L) ] = 0
\end{displaymath}](img343.png) |
(5.106) |
となる。これらの式から半周期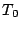 が求められる。この
が求められる。この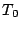 を
(5.104)式に適用すれば、振幅が求められる。
を
(5.104)式に適用すれば、振幅が求められる。
[例]オン・オフ・サーボ系
図5.26のようなオン・オフ・サーボ系にステップ入力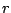 が加わっ
た場合を考える。
が加わっ
た場合を考える。
状態方程式は
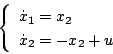 |
(5.107) |
となるから
であり、
![\begin{displaymath}
e^{\mbox{\boldmath$A$} t} =
\left[
\begin{array}{cc}
1 &...
...begin{array}{c}
t-1+e^{-t} \\
1-e^{-t}
\end{array} \right]
\end{displaymath}](img348.png) |
(5.108) |
となる。したがって
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(t) \\
x_2(t)
\end{array} \...
...begin{array}{c}
t-1+e^{-t} \\
1-e^{-t}
\end{array} \right]
\end{displaymath}](img349.png) |
(5.109) |
となる。
この応答波形は大体図5.27のようになる。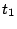 時間までの間は、
時間までの間は、
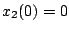 とした場合
とした場合
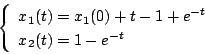 |
(5.110) |
となり、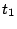 時点で
時点で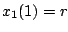 となる。ゆえに
となる。ゆえに
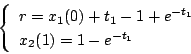 |
(5.111) |
と書ける。上の式から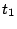 が求まれば、下の式より
が求まれば、下の式より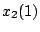 が求まる。ここで
オン・オフ切り換えが行われ、次の
が求まる。ここで
オン・オフ切り換えが行われ、次の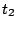 時間の間は
時間の間は
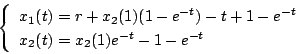 |
(5.112) |
の応答をし、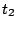 時点で
時点で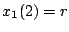 となるので
となるので
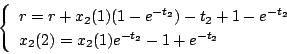 |
(5.113) |
と書ける。上の式から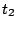 が求まれば、下の式より
が求まれば、下の式より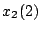 が求まる。このように
して次々と計算を進めて行けば、過渡応答の厳密な解が得られる。
が求まる。このように
して次々と計算を進めて行けば、過渡応答の厳密な解が得られる。
この経過の最後の定常状態でリミットサイクルに入る。(5.104)式に
(5.110)式を適用すると
![\begin{displaymath}
\mbox{\boldmath$x$} (0) = -
\left[
\begin{array}{cc}
2 &...
...rray}{c}
T_0 -1+e^{-T_0} \\
1-e^{-T_0}
\end{array} \right]
\end{displaymath}](img362.png) |
(5.114) |
となる。
![\begin{displaymath}
\left[
\begin{array}{cc}
2 & 1-e^{-T_0} \\
0 & 1+e^{-T_...
...e^{-T_0} } \\
0 & \frac {1}{1+e^{-T_0}}
\end{array} \right]
\end{displaymath}](img363.png) |
(5.115) |
であるから
![\begin{displaymath}
\mbox{\boldmath$x$} (0)=
- \left[
\begin{array}{c}
{\dis...
...\
{\displaystyle - \tanh \frac{T_0}{2}}
\end{array} \right]
\end{displaymath}](img364.png) |
(5.116) |
となる。また図5.26より
![\begin{displaymath}
\mbox{\boldmath$c$} ^T =
\left[
\begin{array}{cc}
1 & 0
\end{array} \right]
\end{displaymath}](img365.png) |
(5.117) |
であるから、(5.106)式より
したがって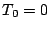 となり、これは周期0、すなわち無限大の周波数のリミットサ
イクルとなることを意味している。
となり、これは周期0、すなわち無限大の周波数のリミットサ
イクルとなることを意味している。
もしむだ時間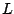 があるとすると、(5.108)式より
があるとすると、(5.108)式より
| |
|
![$\displaystyle \frac{T_0}{2} - (T_0 - L)+1-e^{-(T_0-L)} \left[ 1+ \tanh \frac{T_0}{2}
\right]$](img370.png) |
|
| |
|
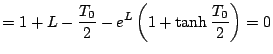 |
(5.119) |
となるので、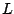 を与えれば
を与えれば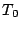 が求まる。その
が求まる。その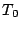 を(5.118)式に適用すると
リミットサイクルの振幅も求まることになる。
を(5.118)式に適用すると
リミットサイクルの振幅も求まることになる。


Next: 最短時間オン・オフ制御
Up: 断片的線形化法
Previous: 一次遅れ系のオン・オフ制御
Yasunari SHIDAMA
平成15年7月28日
![]() であるから
であるから
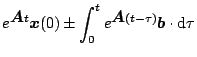
![]() としたとき、オンの区間のみを考えると
としたとき、オンの区間のみを考えると
![]() は
は
![]() が加わっ
た場合を考える。
が加わっ
た場合を考える。
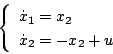
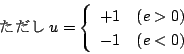
![\begin{displaymath}\mbox{\boldmath$A$} = \left[
\begin{array}{cc}
0 & 1 \\
0 & ...
...ath$b$} = \left[
\begin{array}{c}
0 \\
1
\end{array}
\right] \end{displaymath}](img347.png)
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(t) \\
x_2(t)
\end{array} \...
...begin{array}{c}
t-1+e^{-t} \\
1-e^{-t}
\end{array} \right]
\end{displaymath}](img349.png)
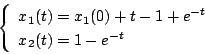
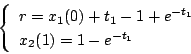
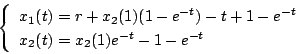
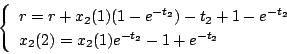
![\begin{displaymath}
\mbox{\boldmath$x$} (0) = -
\left[
\begin{array}{cc}
2 &...
...rray}{c}
T_0 -1+e^{-T_0} \\
1-e^{-T_0}
\end{array} \right]
\end{displaymath}](img362.png)
![\begin{displaymath}
\left[
\begin{array}{cc}
2 & 1-e^{-T_0} \\
0 & 1+e^{-T_...
...e^{-T_0} } \\
0 & \frac {1}{1+e^{-T_0}}
\end{array} \right]
\end{displaymath}](img363.png)
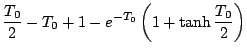
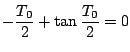
![]() があるとすると、(5.108)式より
があるとすると、(5.108)式より
![$\displaystyle \frac{T_0}{2} - (T_0 - L)+1-e^{-(T_0-L)} \left[ 1+ \tanh \frac{T_0}{2}
\right]$](img370.png)