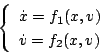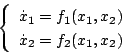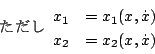Next: 位相面軌道の描き方
Up: 状態面及び位相面解析
Previous: 状態面及び位相面解析
状態変数を各座標軸にとった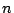 次元空間を状態空間という。システムのある時
点における状態は状態空間の一つの点として表され、これを状態点という。状態
が変化るすにともなって状態点は移動し軌跡を描く。これを軌道という。軌道は
初期条件を与えることによって描くことができる。
次元空間を状態空間という。システムのある時
点における状態は状態空間の一つの点として表され、これを状態点という。状態
が変化るすにともなって状態点は移動し軌跡を描く。これを軌道という。軌道は
初期条件を与えることによって描くことができる。
状態空間のうち特殊な場合、すなわち状態変数を相変数にとった場合、これを位
相空間という。また2次のシステムの場合は状態面(位相面)となる。多次元の
空間を考えることは容易ではないので、通常は2次のシステムを状態面(位相面)
として取り扱うことが多い。
状態面(位相面)解析はこの軌道を描き、その形を調べることによって系の動的
な性質を解析する方法で、線形系のみならず、微分方程式の係数が状態変数の関
数となるような非線形空間にも適用される。(ただし時変系には適用されない)
すなわち
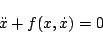 |
(5.148) |
または
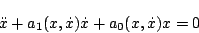 |
(5.149) |
のような形のものに適用される。
位相面解析の場合は(5.150)式を
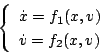 |
(5.150) |
のような形で取り扱う。また状態面解析の場合は
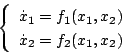 |
(5.151) |
のような形で取り扱う。一般にベクトルとしては
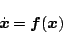 |
(5.152) |
ここに
![$ \mbox{\boldmath$x$} = [x,\dot{x} ]^Tまたは\mbox{\boldmath$x$} = [x_1,x_2]^T $](img451.png) で表示する。
で表示する。
通常インパルス、ステップ、ランプ、等加速度などの入力に対する応答を見るの
に適用される。
3次元の状態空間による解析も行われるが、非常に複雑となる。高次のシステム
は、むしろ適当な省略によって2次系として解析が行われる。
たとえば
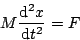 |
(5.153) |
というようなシステムの場合
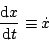 |
(5.154) |
とすると
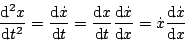 |
(5.155) |
となるから、(5.155)式は
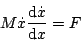 |
(5.156) |
となり
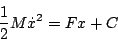 |
(5.157) |
となる。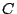 は積分定数であり、初期条件によって決定される。
(5.159)式は
は積分定数であり、初期条件によって決定される。
(5.159)式は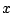 と
と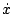 との関係を示しているから、
との関係を示しているから、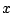 を横軸、
を横軸、
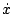 を縦軸にとった位相面に
を縦軸にとった位相面に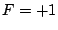 と
と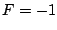 の場合を描くと図
5.29のようになり、これが(5.155)式のシステムの位相面軌
道である。初期条件
の場合を描くと図
5.29のようになり、これが(5.155)式のシステムの位相面軌
道である。初期条件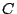 のとり方によって横軸に平行移動する形となる。
のとり方によって横軸に平行移動する形となる。



Next: 位相面軌道の描き方
Up: 状態面及び位相面解析
Previous: 状態面及び位相面解析
Yasunari SHIDAMA
平成15年7月28日