


Next: 二次遅れ系の場合
Up: 状態面及び位相面解析
Previous: プロセス系のオン・オフ制御
図5.35に示すようなサーボ系を3位置のオン・オフ制御をする場合を考える。
制御方程式は
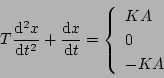 |
(5.175) |
となる。ステップ入力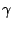 に対し偏差
に対し偏差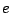 は
は
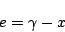 |
(5.176) |
であるから(5.177)式は
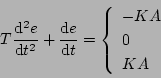 |
(5.177) |
と書き直せる。そしていま
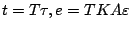 と置いて無次元化すると
と置いて無次元化すると
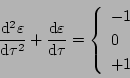 |
(5.178) |
となる。
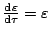 とすると
とすると
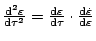 となるので上式は次のように書き直せる。
となるので上式は次のように書き直せる。
さらにこの式は
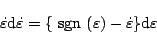 |
(5.180) |
となり、
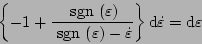 |
(5.181) |
が得られる。これを積分して
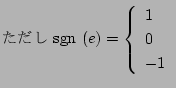
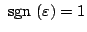 の時
の時
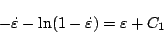 |
(5.182) |
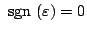 のとき
のとき
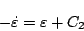 |
(5.183) |
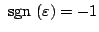 のとき
のとき
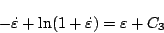 |
(5.184) |
が位相面軌道となる。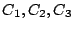 は初期値によって定まる定数である。図
5.36は初期値が0の場合の各軌道を示している。初期値のある場合は、
これらが横に水平移動した形となる。
は初期値によって定まる定数である。図
5.36は初期値が0の場合の各軌道を示している。初期値のある場合は、
これらが横に水平移動した形となる。
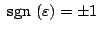 の時の経過時間は(5.180)式を積分して
の時の経過時間は(5.180)式を積分して
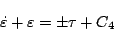 |
(5.185) |
となり、
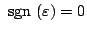 のときは
のときは
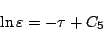 |
(5.186) |
となる。図5.37は時間スケールを示し、
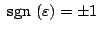 の場合は
の場合は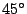 斜線上等間隔で、また
斜線上等間隔で、また
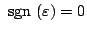 は
は
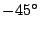 斜線上に対数間隔で測られる。同図の目盛りは前者は原点からの、
後者は
斜線上に対数間隔で測られる。同図の目盛りは前者は原点からの、
後者は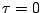 と書いてある点からの無次元空間を示している。時間スケー
ルも横に水平移動できるので、軌道上のある位置から次の位置までの経過時間は、
このスケールを移動させながら測ることができる。
と書いてある点からの無次元空間を示している。時間スケー
ルも横に水平移動できるので、軌道上のある位置から次の位置までの経過時間は、
このスケールを移動させながら測ることができる。
図5.38はデッドゾーン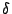 、ヒステリシス
、ヒステリシス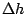 を持つオ
ン・オフ制御系の位相面軌道を示したものである。初期値
を持つオ
ン・オフ制御系の位相面軌道を示したものである。初期値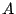 から出発し、最初
(5.186)式の軌道を描き、デッドゾーンに入ったとき(5.185)
式の軌道となり、デッドゾーンから出たら(5.184)式の軌道になる。
さらに再びデッドゾーンに入って(5.185)式の軌道となり、以下これ
を繰り返す。同図は最終的にはリミットサイクルになっていることを示している。
から出発し、最初
(5.186)式の軌道を描き、デッドゾーンに入ったとき(5.185)
式の軌道となり、デッドゾーンから出たら(5.184)式の軌道になる。
さらに再びデッドゾーンに入って(5.185)式の軌道となり、以下これ
を繰り返す。同図は最終的にはリミットサイクルになっていることを示している。
初期値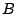 から出発してもやはり同じリミットサイクルとなることがわかる。
から出発してもやはり同じリミットサイクルとなることがわかる。
次にランプ入力が加わった場合を考える。このとき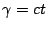 という
形になるので、(5.178)式の代わりに
という
形になるので、(5.178)式の代わりに
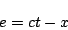 |
(5.187) |
となる。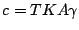 で無次元化すると(5.180)式の代わりに
で無次元化すると(5.180)式の代わりに
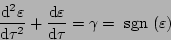 |
(5.188) |
となる。これを書き直すと
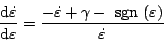 |
(5.189) |
となり、これを積分して、
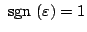 のとき
のとき
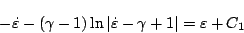 |
(5.190) |
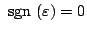 のとき
のとき
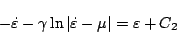 |
(5.191) |
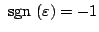 のとき
のとき
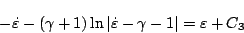 |
(5.192) |
が位相面軌道である。また時間目盛りは
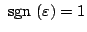 のとき
のとき
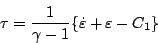 |
(5.193) |
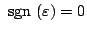 のとき
のとき
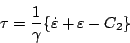 |
(5.194) |
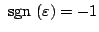 のとき
のとき
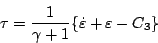 |
(5.195) |
となる。
ステップ入力の場合と似たような形であるが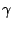 の値によって変わること
がわかる。
の値によって変わること
がわかる。
図5.39は、
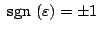 の場合で
の場合で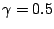 の
ときの位相面軌道を示している。
の
ときの位相面軌道を示している。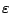 の正側と負側では軌道の形が異
なっている。
の正側と負側では軌道の形が異
なっている。



Next: 二次遅れ系の場合
Up: 状態面及び位相面解析
Previous: プロセス系のオン・オフ制御
Yasunari SHIDAMA
平成15年7月28日
![\includegraphics[scale=0.60]{eps/5-4-8.eps}](img509.png)
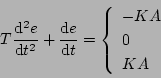
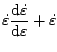
![]() 、ヒステリシス
、ヒステリシス![]() を持つオ
ン・オフ制御系の位相面軌道を示したものである。初期値
を持つオ
ン・オフ制御系の位相面軌道を示したものである。初期値![]() から出発し、最初
(5.186)式の軌道を描き、デッドゾーンに入ったとき(5.185)
式の軌道となり、デッドゾーンから出たら(5.184)式の軌道になる。
さらに再びデッドゾーンに入って(5.185)式の軌道となり、以下これ
を繰り返す。同図は最終的にはリミットサイクルになっていることを示している。
から出発し、最初
(5.186)式の軌道を描き、デッドゾーンに入ったとき(5.185)
式の軌道となり、デッドゾーンから出たら(5.184)式の軌道になる。
さらに再びデッドゾーンに入って(5.185)式の軌道となり、以下これ
を繰り返す。同図は最終的にはリミットサイクルになっていることを示している。
![]() から出発してもやはり同じリミットサイクルとなることがわかる。
から出発してもやはり同じリミットサイクルとなることがわかる。
![]() という
形になるので、(5.178)式の代わりに
という
形になるので、(5.178)式の代わりに
![]() の値によって変わること
がわかる。
の値によって変わること
がわかる。
![]() の場合で
の場合で![]() の
ときの位相面軌道を示している。
の
ときの位相面軌道を示している。![]() の正側と負側では軌道の形が異
なっている。
の正側と負側では軌道の形が異
なっている。