


Next: サーボ系の最短時間制御
Up: 状態面及び位相面解析
Previous: サーボ系のオン・オフ制御
次式で与えられるような二次遅れ系の位相面軌道は斜交軸を用いて描くことができる。
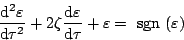 |
(5.196) |
ただし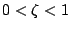 の場合とする。いま
の場合とする。いま
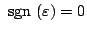 の場合の解は
の場合の解は
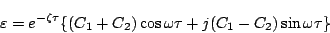 |
(5.197) |
である。ただし、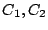 は初期値によって定まる定数であり、
は初期値によって定まる定数であり、
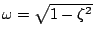 である。
である。
ここで
とおくと上式は
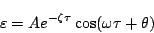 |
(5.198) |
となり、また
が得られる。
いま、図5.40に示すような斜交軸の位相面を考えた場合、余弦の公式より、
次の関係が得られる。
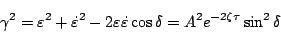 |
(5.200) |
ゆえに
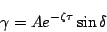 |
(5.201) |
また
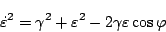 |
(5.202) |
この式に、(5.200)、(5.201)、(5.202)式を代入すると
ゆえに
この式は、図5.41に示すように原点を中心とし、時計方向に回転するスパイラル
を示している。
オン・オフ制御の場合は、それぞれ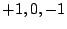 を中心とするスパイラルに、
各切換点において逐次転移をする。
を中心とするスパイラルに、
各切換点において逐次転移をする。
図5.42は
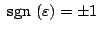 の場合で、最初
の場合で、最初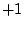 を中心とするスパイラルで始まり、縦軸と交差したところで
を中心とするスパイラルで始まり、縦軸と交差したところで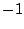 を中心とする
スパイラルに切り換わり、以後同じような切換えが行われる軌道を示している。
を中心とする
スパイラルに切り換わり、以後同じような切換えが行われる軌道を示している。



Next: サーボ系の最短時間制御
Up: 状態面及び位相面解析
Previous: サーボ系のオン・オフ制御
Yasunari SHIDAMA
平成15年7月28日
![]() を中心とするスパイラルに、
各切換点において逐次転移をする。
を中心とするスパイラルに、
各切換点において逐次転移をする。
![]() の場合で、最初
の場合で、最初![]() を中心とするスパイラルで始まり、縦軸と交差したところで
を中心とするスパイラルで始まり、縦軸と交差したところで![]() を中心とする
スパイラルに切り換わり、以後同じような切換えが行われる軌道を示している。
を中心とする
スパイラルに切り換わり、以後同じような切換えが行われる軌道を示している。