


Next: 時変系の場合
Up: 安定判別
Previous: 安定判別
非線形システムが
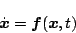 |
(5.206) |
で与えられたとき、
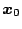 を平衡点の状態ベクトルとして
を平衡点の状態ベクトルとして
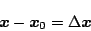 |
(5.207) |
とし、
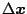 が微小であるとすれば、テーラー展開をして
が微小であるとすれば、テーラー展開をして
上式より
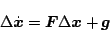 |
(5.209) |
となる。
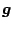 は
は
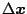 の高次の項を含んだものである。いまリアプノフ関数を
の高次の項を含んだものである。いまリアプノフ関数を
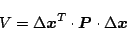 |
(5.210) |
とおいたとき
となるから、上式が負となったとき安定であり、また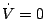 が安定限界で
ある。
が安定限界で
ある。
[例]
いまシステム方程式を
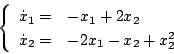 |
(5.212) |
とする。
原点を平衡点とした場合、
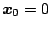 ゆえ
ゆえ
![\begin{displaymath}
\ddot{\mbox{\boldmath$f$}} (\mbox{\boldmath$x$} _0,t) =
\s...
...eft[
\begin{array}{cc}
0 & 0 \\
0 & 2
\end{array} \right]
\end{displaymath}](img604.png) |
(5.214) |
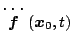 以降は0となるので
以降は0となるので
![\begin{displaymath}
\mbox{\boldmath$g$} = \frac{1}{2!} \ddot{\mbox{\boldmath$f$...
...=
\left[
\begin{array}{c}
0 \\
x_2^2
\end{array} \right]
\end{displaymath}](img606.png) |
(5.215) |
となる。したがって(5.211)式は
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}} = \mbox{\boldmath$Fx$} + \mbox{\b...
...t[
\begin{array}{c}
0 \\
\Delta x_2^2
\end{array} \right]
\end{displaymath}](img607.png) |
(5.216) |
となる。いま
![\begin{displaymath}
\mbox{\boldmath$Q$} = \left[
\begin{array}{cc}
2 & 0 \\
0 & 2
\end{array} \right]
\end{displaymath}](img608.png) |
(5.217) |
とおくと、
ゆえに
より
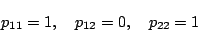 |
(5.219) |
したがって
![\begin{displaymath}
\mbox{\boldmath$P$} =
\left[
\begin{array}{cc}
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{displaymath}](img615.png) |
(5.220) |
となり、(5.213)式は次のようになる。
ゆえに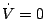 は
は
となり、図5.47で示すこの曲線の下側は安定領域である。
線形近似として扱う場合には、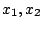 が
が
の円内にあれば安定な微小範囲といえる。



Next: 時変系の場合
Up: 安定判別
Previous: 安定判別
Yasunari SHIDAMA
平成15年7月28日
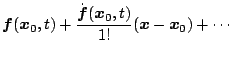
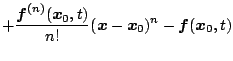
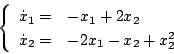
![]() ゆえ
ゆえ
![$\displaystyle \sum ^2 _{i=1}
\frac{\partial}{\partial x_i}
\left[
\begin{array}...
..._1 & 2x_2\\
-2x_1 & -x_2+x_2^2
\end{array}\right] _{\mbox{\boldmath$x$} _0 =0}$](img602.png)
![$\displaystyle \left[
\begin{array}{cc}
-1 & 2\\
-2 & -1+2x_2\\
\end{array}\right]_{x_2 =0}
= \left[
\begin{array}{cc}
-1 & 2 \\
-2 & -1 \\
\end{array}\right]$](img603.png)
![\begin{displaymath}
\ddot{\mbox{\boldmath$f$}} (\mbox{\boldmath$x$} _0,t) =
\s...
...eft[
\begin{array}{cc}
0 & 0 \\
0 & 2
\end{array} \right]
\end{displaymath}](img604.png)
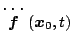 以降は0となるので
以降は0となるので
![\begin{displaymath}
\mbox{\boldmath$g$} = \frac{1}{2!} \ddot{\mbox{\boldmath$f$...
...=
\left[
\begin{array}{c}
0 \\
x_2^2
\end{array} \right]
\end{displaymath}](img606.png)
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}} = \mbox{\boldmath$Fx$} + \mbox{\b...
...t[
\begin{array}{c}
0 \\
\Delta x_2^2
\end{array} \right]
\end{displaymath}](img607.png)
![\begin{displaymath}
\mbox{\boldmath$Q$} = \left[
\begin{array}{cc}
2 & 0 \\
0 & 2
\end{array} \right]
\end{displaymath}](img608.png)
![$\displaystyle \left[
\begin{array}{cc}
-1 & -2 \\
2 & -1
\end{array}\right]
\l...
...end{array}\right]
\left[
\begin{array}{cc}
-1 & 2 \\
-2 & 1
\end{array}\right]$](img610.png)
![$\displaystyle \left[
\begin{array}{cc}
-2p_{11}-4p_{12} & 2p_{11}-2p_{12}-2p_{22} \\
2p_{11}-2p_{12}-2p_{22} & 4p_{12}-2p_{22}
\end{array}\right]$](img611.png)
![$\displaystyle -\mbox{\boldmath$Q$} =
\left[
\begin{array}{cc}
-2 & 0 \\
0 & -2
\end{array}\right]$](img612.png)
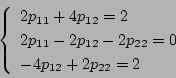
![\begin{displaymath}
\mbox{\boldmath$P$} =
\left[
\begin{array}{cc}
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{displaymath}](img615.png)
![$\displaystyle - \left[
\begin{array}{cc}
x_1 & x_2
\end{array}\right]
\left[
\b...
...0 & 1
\end{array}\right]
\left[
\begin{array}{c}
0 \\
x_2^2
\end{array}\right]$](img616.png)
![]() が
が