Next: Krasovskiiの方法
Up: 安定判別
Previous: 時変系の場合
非線形オートノマス系の場合
与えられた非線形系が
で、
という形をしている場合に適用する方法である。上式を
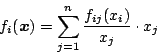 |
(5.239) |
と書き直したとき、その極限
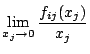 が存在すると仮定する。そこで
が存在すると仮定する。そこで
とおくと、(5.239)式は
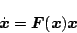 |
(5.241) |
と書ける。上式の
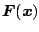 の要素が
の要素が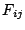 である。
である。
いま、リアプノフ関数を
とおき、その微係数をとると
となる。
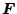 が正定で
が正定で
![\begin{displaymath}[\mbox{\boldmath$F$}^T(\mbox{\boldmath$x$}))\mbox{\boldmath$P...
...mbox{\boldmath$x$})]=-\mbox{\boldmath$Q$}(\mbox{\boldmath$x$})
\end{displaymath}](img673.png) |
(5.244) |
が負定なら漸近安定となる。
[例]
いま図5.48に示すシステムの安定を判別する。
(5.243)式によりシステム方程式を
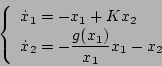 |
(5.245) |
と表す。したがって
![\begin{displaymath}
\mbox{\boldmath$F$}= \left[
\begin{array}{cc}
-1 & K \\
{\displaystyle -\frac{g(x_1)}{x_1}} & -1
\end{array}\right]
\end{displaymath}](img676.png) |
(5.246) |
である。いま
![\begin{displaymath}
\mbox{\boldmath$P$} = \left[
\begin{array}{cc}
p_{11} & 0 \\
0 & p_{22}
\end{array}\right]
\end{displaymath}](img677.png) |
(5.247) |
としたとき
となるから、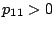 で、かつ
で、かつ
![\begin{displaymath}
4p_{11}p_{22}-\left[p_{22} \frac{g(x_1)}{x_1}-Kp_{11}\right]^2 > 0
\end{displaymath}](img682.png) |
(5.249) |
であれば安定となる。そこで
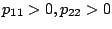 のとき
のとき
![\begin{displaymath}
4p_{11}p_{22}-\left[p_{22} \frac{g(x_1)}{x_1}-Kp_{11}\right]^2 = 0
\end{displaymath}](img684.png) |
(5.250) |
として
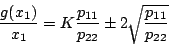 |
(5.251) |
となるから、
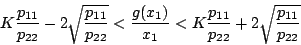 |
(5.252) |
であれば安定である。そこで、例えば
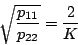 |
(5.253) |
とした場合
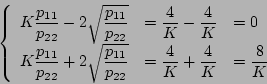 |
(5.254) |
となるから
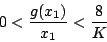 |
(5.255) |
が安定の条件で、図5.49に示す領域に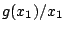 があればよい。
があればよい。



Next: Krasovskiiの方法
Up: 安定判別
Previous: 時変系の場合
Yasunari SHIDAMA
平成15年7月28日
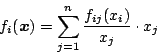
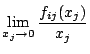 が存在すると仮定する。そこで
が存在すると仮定する。そこで
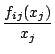
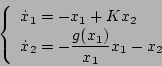
![\begin{displaymath}
\mbox{\boldmath$F$}= \left[
\begin{array}{cc}
-1 & K \\
{\displaystyle -\frac{g(x_1)}{x_1}} & -1
\end{array}\right]
\end{displaymath}](img676.png)
![\begin{displaymath}
\mbox{\boldmath$P$} = \left[
\begin{array}{cc}
p_{11} & 0 \\
0 & p_{22}
\end{array}\right]
\end{displaymath}](img677.png)
![$\displaystyle \left[
\begin{array}{cc}
-1 & K \\
{\displaystyle -\frac{g(x_1)}...
...ray}{cc}
-1 & K \\
{\displaystyle -\frac{g(x_1)}{x_1}} & -1
\end{array}\right]$](img679.png)
![$\displaystyle \left[
\begin{array}{cc}
-2p_{11} & {\displaystyle -\frac{g(x_1)}...
...{\displaystyle -\frac{g(x_1)}{x_1}p_{22}}+Kp_{11} & -2p_{22}
\end{array}\right]$](img680.png)