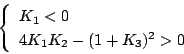Next: 可変傾斜法(Variable gradient method)
Up: 安定判別
Previous: Krasovskiiの方法
図5.51に示すような、フィードバックに非線形要素が含まれているシステムの
安定判別を行う方法である。
この場合のシステム方程式は
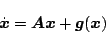 |
(5.274) |
で表される。(3)項と同様に
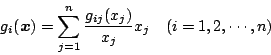 |
(5.275) |
とし
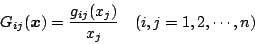 |
(5.276) |
としたとき
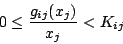 |
(5.277) |
のように
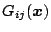 が
が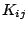 という定数値以下と仮定する。その場合、
システム方程式
という定数値以下と仮定する。その場合、
システム方程式
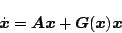 |
(5.278) |
を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}=\mbox{\boldmath$Ax$}+\mbox{\boldm...
...}=[\mbox{\boldmath$A$}+\mbox{\boldmath$K$}]\mbox{\boldmath$x$}
\end{displaymath}](img734.png) |
(5.279) |
と置いて、リアプノフ関数を
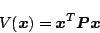 |
(5.280) |
とした場合
![\begin{displaymath}
\dot{V} = \mbox{\boldmath$x$}^T[(\mbox{\boldmath$A$}+\mbox{...
...}(\mbox{\boldmath$A$}+\mbox{\boldmath$K$})]\mbox{\boldmath$x$}
\end{displaymath}](img736.png) |
(5.281) |
となるから
![\begin{displaymath}[(\mbox{\boldmath$A$}+\mbox{\boldmath$K$})^T\mbox{\boldmath$P...
...box{\boldmath$A$}+\mbox{\boldmath$K$})]= - \mbox{\boldmath$Q$}
\end{displaymath}](img737.png) |
(5.282) |
として線形系と同じように安定判別が行える。
[例]
システム方程式が
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{array}\...
...t[
\begin{array}{c}
g_1(x_1)+g_3(x_2) \\
0
\end{array}\right]
\end{displaymath}](img738.png) |
(5.283) |
の場合で、
という条件のとき、
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{array}\...
...\right] \left[
\begin{array}{c}
x_1 \\
x_2
\end{array}\right]
\end{displaymath}](img743.png) |
(5.286) |
という線形系におきかえると、(5.281)式より
![\begin{displaymath}
-\mbox{\boldmath$Q$}=\left[
\begin{array}{cc}
2K_1p_{11}+2p_...
...22}+(K_1+K_2)p_{12} & 2K_2p_{22}+2K_3p_{12}
\end{array}\right]
\end{displaymath}](img744.png) |
(5.287) |
となる。
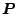 が正定対称となるように、
が正定対称となるように、
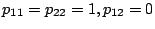 とおくと
とおくと
![\begin{displaymath}
- \mbox{\boldmath$Q$}=\left[
\begin{array}{cc}
2K_1 & K_3+1 \\
K_3+1 & 2K_2
\end{array}\right]
\end{displaymath}](img746.png) |
(5.288) |
となるから
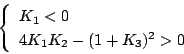 |
(5.289) |
が安定の条件となる。下の条件を満足するために当然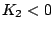 である。
である。



Next: 可変傾斜法(Variable gradient method)
Up: 安定判別
Previous: Krasovskiiの方法
Yasunari SHIDAMA
平成15年7月28日
![\includegraphics[scale=0.60]{eps/5-5-5.eps}](img725.png)
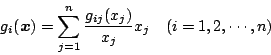
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{array}\...
...t[
\begin{array}{c}
g_1(x_1)+g_3(x_2) \\
0
\end{array}\right]
\end{displaymath}](img738.png)
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{array}\...
...\right] \left[
\begin{array}{c}
x_1 \\
x_2
\end{array}\right]
\end{displaymath}](img743.png)
![\begin{displaymath}
-\mbox{\boldmath$Q$}=\left[
\begin{array}{cc}
2K_1p_{11}+2p_...
...22}+(K_1+K_2)p_{12} & 2K_2p_{22}+2K_3p_{12}
\end{array}\right]
\end{displaymath}](img744.png)
![\begin{displaymath}
- \mbox{\boldmath$Q$}=\left[
\begin{array}{cc}
2K_1 & K_3+1 \\
K_3+1 & 2K_2
\end{array}\right]
\end{displaymath}](img746.png)