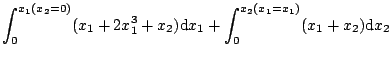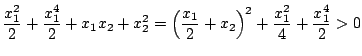Next: Lureの方法
Up: 安定判別
Previous: Aizermanの方法
この方法は、リアプノフ関数を系統的に決定する手法である。いまシステム方程式を
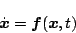 |
(5.290) |
とし、平衡点は原点にあるものとする。またリアプノフ関数を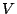 としたとき、
これは
としたとき、
これは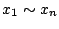 の状態変数を陽に含んでおり、また時間
の状態変数を陽に含んでおり、また時間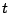 を陽に含んで
いないものとする。そうすると
を陽に含んで
いないものとする。そうすると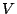 の全微分を求めると
の全微分を求めると
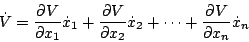 |
(5.291) |
となる。上式を
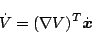 |
(5.292) |
と書く。ここに
![\begin{displaymath}
(\nabla V)^T = \left[ \frac{\partial V}{\partial x_1} \cdot...
...tial V}{\partial x_n}\right] =
[\nabla V_1,\cdots,\nabla V_n]
\end{displaymath}](img752.png) |
(5.293) |
である。このようにしたとき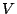 、は
、は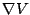 の線形積分として得られる。
の線形積分として得られる。
すなわち
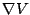 の線形積分から一義的に決定されるスカラー関数
の線形積分から一義的に決定されるスカラー関数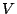 に対し、
に対し、
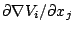 によって得られる次の行列
によって得られる次の行列
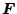 は対称となる。
は対称となる。
![\begin{displaymath}
\mbox{\boldmath$F$}= \left[
\begin{array}{cccc}
{\displaysty...
...e \frac{\partial \nabla V_n}{\partial x_n}}
\end{array}\right]
\end{displaymath}](img759.png) |
(5.295) |
したがって、たとえば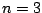 の場合
の場合
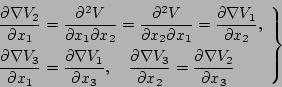 |
(5.296) |
である。
いま
![\begin{displaymath}
\nabla V=
\left[
\begin{array}{c}
a_{11}x_1+a_{12}x_2+\c...
...\\
a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n
\end{array} \right]
\end{displaymath}](img762.png) |
(5.297) |
とおく。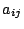 は未定の量であるが、定数か時間関数または状態変数の関数で
ある。しかしこのうち
は未定の量であるが、定数か時間関数または状態変数の関数で
ある。しかしこのうち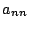 のみは定数か、時間関数に選ぶ。
のみは定数か、時間関数に選ぶ。
そこで、次のような手順で安定の判別を行う。
- step 1.
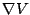 を(5.299)式のようにとる。
を(5.299)式のようにとる。
- step 2.
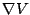 から(5.294)式によって
から(5.294)式によって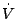 を決定する。
を決定する。
- step 3.
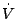 は負定または準負定になるように
は負定または準負定になるように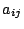 を仮定する。
を仮定する。
- step 4.
- (5.297)式の
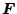 が対称であることを用いて
が対称であることを用いて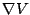 の残りの未知係数を決定する。
の残りの未知係数を決定する。
- step 5.
- step 4の計算でstep 3の過程の変更を必要とするか否かを再検討する。
- step 6.
- (5.296)式より
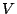 を決定する。
を決定する。
- step 7.
- 漸近安定の範囲を調べる。
[例]
システム方程式が
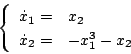 |
(5.298) |
の場合、安定を判別する。
- step 1.
-
![\begin{displaymath}
\nabla V=\left[
\begin{array}{c}
a_{11}x_1+a_{12}x_2 \\
a_{21}x_1+2x_2
\end{array} \right]
\end{displaymath}](img765.png) |
(5.299) |
- step 2.
-
- step 3.
- いま
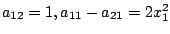 とおくと
とおくと
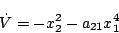 |
(5.301) |
となり、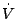 は
は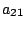 が正なら負定である。
が正なら負定である。
- step 4.
- ゆえに
![\begin{displaymath}
\nabla V=
\left[
\begin{array}{c}
a_{21}x_1+2x_1^3+x_2 \\
a_{21}x_1+2x_2
\end{array} \right]
\end{displaymath}](img771.png) |
(5.302) |
となるから、(5.298)式より
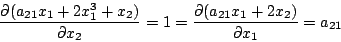 |
(5.303) |
となり、
![\begin{displaymath}
\nabla V=
\left[
\begin{array}{c}
x_1+2x_1^3+x_2 \\
x_1+2x_2
\end{array} \right]
\end{displaymath}](img773.png) |
(5.304) |
となる。
- step 5.
- (5.303)式は
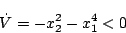 |
(5.305) |
となり、明らかに負である。
- step 6.
-
すなわちリアプノフ関数は正である。
- step 7.
- この場合、条件なしの大局的漸近安定である。



Next: Lureの方法
Up: 安定判別
Previous: Aizermanの方法
Yasunari SHIDAMA
平成15年7月28日
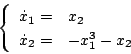
![\begin{displaymath}
\nabla V=\left[
\begin{array}{c}
a_{11}x_1+a_{12}x_2 \\
a_{21}x_1+2x_2
\end{array} \right]
\end{displaymath}](img765.png)
![$\displaystyle [(a_{11}x_1+a_{12}x_2)(a_{21}x_1+2x_2)]
\left[
\begin{array}{c}
x_2 \\
-x^3_1-x_2
\end{array}\right]$](img766.png)
![\begin{displaymath}
\nabla V=
\left[
\begin{array}{c}
a_{21}x_1+2x_1^3+x_2 \\
a_{21}x_1+2x_2
\end{array} \right]
\end{displaymath}](img771.png)
![\begin{displaymath}
\nabla V=
\left[
\begin{array}{c}
x_1+2x_1^3+x_2 \\
x_1+2x_2
\end{array} \right]
\end{displaymath}](img773.png)