Next: この文書について...
Up: 安定判別
Previous: 可変傾斜法(Variable gradient method)
図5.52に示すようなシステムにおいて、線形要素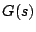 の極がすべて
左半面にありかつ0の極を含まず、また非線形要素
の極がすべて
左半面にありかつ0の極を含まず、また非線形要素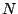 は連続的で、非線形要素へ
の入力
は連続的で、非線形要素へ
の入力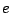 の関数となっており、しかも
の関数となっており、しかも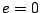 のとき、その出力
のとき、その出力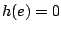 である場合
にこの方法は適用される。なお
である場合
にこの方法は適用される。なお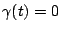 とする。
とする。
システム方程式を正準形で表示すると
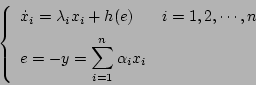 |
(5.307) |
となる。ここに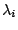 は
は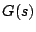 の極であり、
の極であり、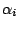 は
は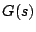 を
部分分数に分解したときの各係数の負の値である。
を
部分分数に分解したときの各係数の負の値である。
上式より
(5.309)式をベクトルで書くと
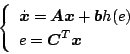 |
(5.309) |
となり、(5.310)式をベクトルで書くと
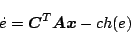 |
(5.310) |
となる。そこで、もし次の条件が成立するなら、システムは大局的漸近安定である。
- (1).
-
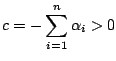
- (2).
-
- (3).
- 次のマトリクスを満足する
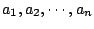 の一組が存在する。
の一組が存在する。
![\begin{displaymath}
\left[
\begin{array}{c}
{\displaystyle 2\sqrt{c}a_1-2 \sum^n...
...egin{array}{c}
0 \\
0 \\
\vdots \\
0 \\
\end{array}\right]
\end{displaymath}](img795.png) |
(5.311) |
ここに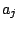 は
は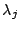 が実数のとき実数であり、
が実数のとき実数であり、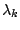 および
および
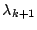 が共役複素数のとき、
が共役複素数のとき、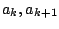 は共役複素数である。
したがって上式は次のように書くこともできる。
は共役複素数である。
したがって上式は次のように書くこともできる。
![\begin{displaymath}
\left[
\begin{array}{c}
{\displaystyle 2\sqrt{c}\bar{a}_1-2\...
...[
\begin{array}{c}
0 \\
0 \\
\vdots \\
0
\end{array}\right]
\end{displaymath}](img801.png) |
(5.312) |
これをベクトルで表すと
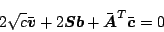 |
(5.313) |
ただし
上式の共役転置をとると
いまリアプノフ関数を次のように選ぶ。
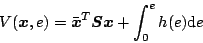 |
(5.315) |
この式は正定である。なぜなら条件として
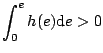 であり
であり
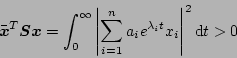 |
(5.316) |
であるから。そこで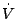 を求めると
を求めると
となる。ここで
となるので、
(5.316)式より最後の項は0となるから
![\begin{displaymath}
\dot{V} =
-\overline{[\mbox{\boldmath$v$}^T\mbox{\boldmath...
...box{\boldmath$v$}^T\mbox{\boldmath$x$}+\sqrt{c}h(e)\right] < 0
\end{displaymath}](img820.png) |
(5.320) |
となり、負となる。したがって前述の条件を満足すれば安定となる。
[例]
システム方程式が
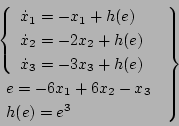 |
(5.321) |
で表される場合の安定判別を行う。
この場合
である。
- (1).
-
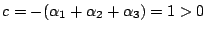
ゆえ第1の条件を満足している。
- (2).
-
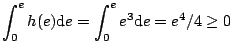
であり、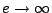 のとき
のとき
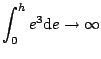 、
、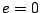 のとき
のとき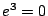 ゆえ第2の条件も満足している。
ゆえ第2の条件も満足している。
- (3).
- (5.313)式は
となり
より
となる。
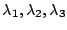 が実数であり、
が実数であり、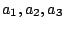 が実数で求まったから、このシステムは安定である。
が実数で求まったから、このシステムは安定である。



Next: この文書について...
Up: 安定判別
Previous: 可変傾斜法(Variable gradient method)
Yasunari SHIDAMA
平成15年7月28日
![\includegraphics[scale=0.60]{eps/5-5-6.eps}](img782.png)
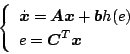
![\begin{displaymath}
ただし、\mbox{\boldmath$A$}=\left[
\begin{array}{cccc}
\lamb...
...a _1 \\
\alpha _2 \\
\vdots \\
\alpha _n
\end{array}\right]
\end{displaymath}](img790.png)
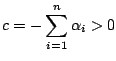
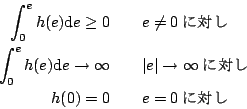
![\begin{displaymath}
\left[
\begin{array}{c}
{\displaystyle 2\sqrt{c}\bar{a}_1-2\...
...[
\begin{array}{c}
0 \\
0 \\
\vdots \\
0
\end{array}\right]
\end{displaymath}](img801.png)
![\begin{displaymath}
\bar{\mbox{\boldmath$v$}}=\left[
\begin{array}{c}
\bar{a}_1 ...
...\bar{a}_na_n}{\bar{\lambda} _n+\lambda _n}}
\end{array}\right]
\end{displaymath}](img804.png)
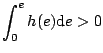 であり
であり
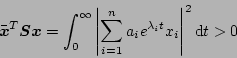
![$\displaystyle -\left[
\begin{array}{cccc}
\bar{a}_1a_1 & \bar{a}_1a_2 & \ldots ...
...cdot \\
\bar{a}_na_1 & \bar{a}_na_2 & \ldots & \bar{a}_na_n
\end{array}\right]$](img814.png)
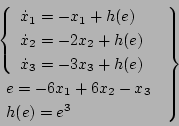
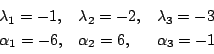
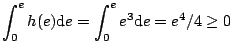
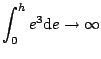 、
、![\begin{displaymath}
\left[
\begin{array}{c}
{\displaystyle 2a_1-2\left(-\frac{a_...
...ght]=
\left[
\begin{array}{c}
0 \\
0 \\
0
\end{array}\right]
\end{displaymath}](img828.png)