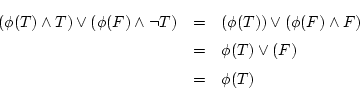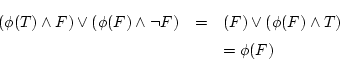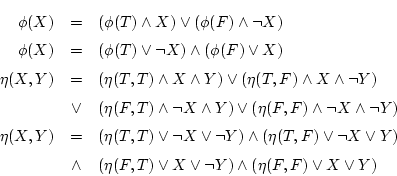

: 変数式の標準形
: 標準形
: 標準形
先に述べたように真理関数を表わす(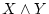 とか
とか
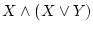 などの)式を、(命題論理における)論理式という。
などの)式を、(命題論理における)論理式という。
一変数の真理関数については
| |
|
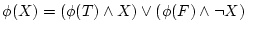 |
(1.7) |
| |
|
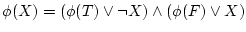 |
(1.8) |
が成り立っている。実際,第(1.7)式について調べると
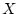 に
に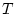 を代入すれば左辺は
を代入すれば左辺は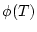 であり,
右辺は定理1.2の等式を使って
であり,
右辺は定理1.2の等式を使って
となり一致する。同様に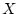 に
に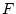 を代入すれば左辺は
を代入すれば左辺は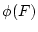 であり,
右辺は定理1.2の等式を使って
であり,
右辺は定理1.2の等式を使って
となる。
第(1.8)式も全く同様である。
第(1.7)式を用いれば,2変数の真理関数
が得られる。同様に第(1.8)式を用いると先ず
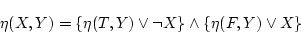 |
(1.10) |
を得る。次に少し複雑であるが定理1.2の分配法則
により
と
を得る。これらから,
を得る。
以上の結果を定理としてまとめておこう。
- 定理2.1
-
以下の等式が成り立つ。

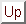

: 変数式の標準形
: 標準形
: 標準形
Yasunari SHIDAMA