

: 演習9
: 演習の解答
: 演習7
- 命題8
-
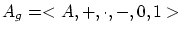 をブール代数とし,
をブール代数とし, 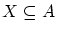 とする.
そのとき,次の(1)〜(3)は同値となる:
とする.
そのとき,次の(1)〜(3)は同値となる:
- (1)は(1)
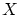 は
は 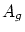 の部分宇宙である;
の部分宇宙である;
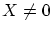 であって,
であって, 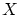 は
は 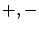 について閉じている;
について閉じている;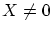 であって,
であって, 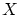 は
は 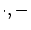 について閉じている.
について閉じている.
(命題8の終わり)
- [証明]
- 定義から
- (1)
- なら (2),(3)は定義から明らか.
- (2)
- なら
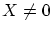 で少なくとも
で少なくとも 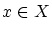 となる元が1つ存在.
となる元が1つ存在.
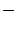 について閉じているから
について閉じているから 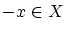 で ,
で ,
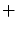 について閉じているから
について閉じているから 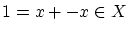
また 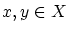 について
について
よって
ゆえに
従って 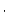 について閉じている.
について閉じている.
さらに
結局,
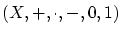 は部分代数.
は部分代数.
全く同様に
- (3)
- なら
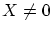 で少なくとも
で少なくとも 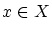 となる元が1つ存在.
となる元が1つ存在.
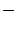 について閉じているから
について閉じているから 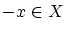 で ,
で ,
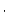 について閉じているから
について閉じているから
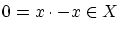
また 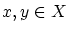 について
について
よって
ゆえに
従って 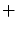 について閉じている.
について閉じている.
さらに
結局,
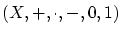 は部分代数.
は部分代数.
[証明終]
- 命題9
-
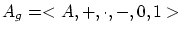 をブール代数とする.
をブール代数とする. 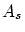 を
を 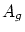 の部分宇宙を
要素とする空でない集合とすると,
の部分宇宙を
要素とする空でない集合とすると, 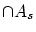 は,
は, 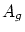 の部分宇宙である.
の部分宇宙である.
(命題9の終わり)
- [証明]
- まず,
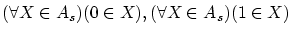 より
より
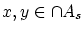 とすると:
とすると:
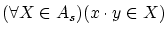 で
で
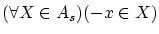 で
で
[証明終]


: 演習9
: 演習の解答
: 演習7
Yasunari SHIDAMA
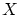 は
は 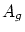 の部分宇宙である;
の部分宇宙である;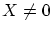 であって,
であって, 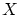 は
は 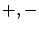 について閉じている;
について閉じている;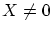 であって,
であって, 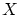 は
は 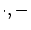 について閉じている.
について閉じている.