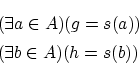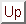

: この文書について...
: ストーンの同型定理
: 上のブール代数の構造
 がブール代数として、
がブール代数として、  が
が  上のブール代数の真の
フィルターというのは
上のブール代数の真の
フィルターというのは
 は
は  上の真のフィルター
上の真のフィルター 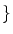 は順序「
は順序「 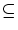 」ついて帰納的順序集合
」ついて帰納的順序集合
- [証明]
- まず,
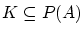 で,
で, 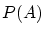 は
は 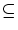 について順序集合なので,
について順序集合なので,
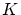 も順序集合.
次に
も順序集合.
次に 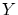 が順序
が順序 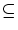 での
での 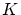 の空でない全順序部分集合とすると,
の空でない全順序部分集合とすると,
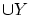 は
は  上の真のフィルター
上の真のフィルター
- (証明)
- (F1)
-
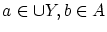 を任意にとって,
を任意にとって, 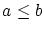 とすると
とすると
 から
から
このような 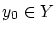 を選ぶと,
を選ぶと, 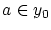 と
と 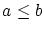 から,
から,
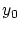 は真のフィルターだから,
は真のフィルターだから,
よって
ゆえに
 となり
となり
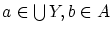 は任意にとったから
は任意にとったから
- (F2)
-
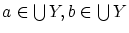 を任意にとると,
を任意にとると,
このような
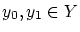 を選んで,
を選んで,
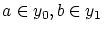 とすると
とすると
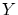 は
は  について全順序だったから
について全順序だったから
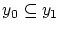 または
または
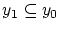 ここで
ここで
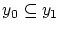 の場合を考えると
の場合を考えると
よって
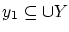 だから
だから
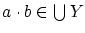
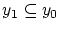 の場合も全く同じ.
の場合も全く同じ.
結局
- (F3)
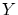 は空でないから
は空でないから
このような 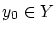 を選べば
を選べば 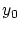 は真のフィルターだから
は真のフィルターだから
よって
ゆえに
- (F4)
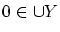 とすると
とすると
このような 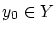 を選ぶと
を選ぶと 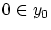 であり,しかし
であり,しかし 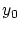 は
真のフィルターだから
は
真のフィルターだから
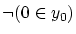 で矛盾.
で矛盾.
(証明終)
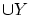 が
が  上の真のフィルターだから
上の真のフィルターだから
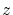 の作り方から明らかに
の作り方から明らかに
よって 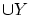 は順序
は順序 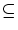 について
について 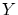 の
の 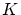 での上界
での上界
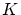 の任意の空でない全順序部分集合
の任意の空でない全順序部分集合 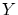 が上界をもつから
が上界をもつから 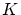 は帰納的
は帰納的
[証明終]
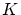 は順序
は順序 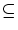 について 帰納的順序集合なのでZornの補題から
極大な元が存在.
について 帰納的順序集合なのでZornの補題から
極大な元が存在.
- (定義3)
-
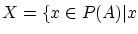 は
は  上の真のフィルター
上の真のフィルター は極大
は極大 
- (定義4)
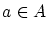 について
について
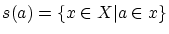 とすると
とすると
が定義できる.
よって写像
が定義される.
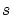 については以下が成り立つ.
については以下が成り立つ.
- (*1)
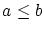 は
は  上の順序関係である.
上の順序関係である.
- (*2)
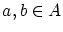 について
について
- (*3)
- 任意の
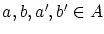 について,
について,
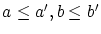 のとき
のとき
- (*4)
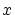 を
を  上の極大な真のフィルターとするとき
上の極大な真のフィルターとするとき
- (*4の証明)
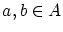 を任意にとり;
を任意にとり;
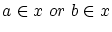 とすると
とすると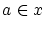 のとき, (*2) から
のとき, (*2) から 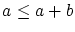 なので
なので 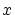 は真の
フィルターなので(F1)から
は真の
フィルターなので(F1)から
同様に 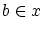 のときも
のときも
逆に 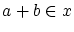 として
として
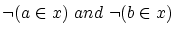 と
すると:
と
すると:
- (証明)(F1)
-
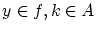 を任意にとり,
を任意にとり, 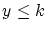 とすると
とすると
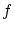 の定義から
の定義から
(*3) から
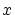 は真のフィルターだから
は真のフィルターだから
よって
- (F2)
-
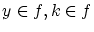 を任意にとると
を任意にとると
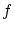 の定義から
の定義から
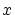 は真のフィルターだから
は真のフィルターだから
よって 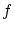 の定義から
の定義から
- (F3)
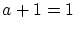
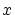 は真のフィルターだから
は真のフィルターだから
よって 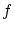 の定義から
の定義から
- (F4)
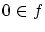 とすると
とすると 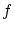 の定義から
の定義から
これは仮定
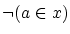 に矛盾.
に矛盾.
よって
(証明終)
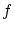 の作り方から
の作り方から
- (証明)
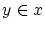 を任意にとると (*2)から
を任意にとると (*2)から 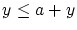 で
で
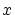 は真のフィルターだから
は真のフィルターだから
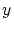 は任意だったから
は任意だったから
よって
一方, 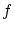 の定義から
の定義から 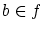 ,仮定から
,仮定から
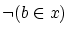 よって
よって
(証明終)
しかし, 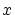 は極大な真のフィルターだったから
は極大な真のフィルターだったから 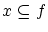 により
により 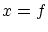 となり矛盾
となり矛盾
(*4の証明終)
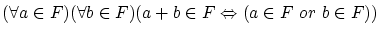 がいえる真のフィルター
がいえる真のフィルター 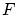 を素フィルターといいます.
を素フィルターといいます.
- (*5)
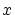 を
を  上の真のフィルターとするとき
上の真のフィルターとするとき
特に 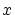 が極大な真のフィルターとするとき
が極大な真のフィルターとするとき
- (*5の証明)
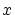 を
を  上の真のフィルターとし
上の真のフィルターとし 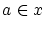 を任意にとると,
を任意にとると,
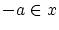 とすると F2から
とすると F2から
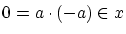 で (F4) の
で (F4) の
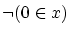 に矛盾
に矛盾
特に 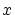 が極大な真のフィルターとするとき
が極大な真のフィルターとするとき
から (*4) により
よって
(*5の証明終)
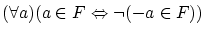 がいえる真のフィルターを超フィルター(ウルトラフィルター)(ultrafilter) と
いいます. 超フィルターは常に
がいえる真のフィルターを超フィルター(ウルトラフィルター)(ultrafilter) と
いいます. 超フィルターは常に 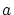 か
か 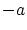 のどちらか一方のみが
のどちらか一方のみが 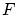 の要素と
なるような真のフィルターです.
の要素と
なるような真のフィルターです.
(*5)は,次の命題に集約されます.
- (命題)
 上の真のフィルター
上の真のフィルター 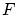 について, 次の
について, 次の 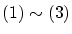 は同値である.
は同値である.
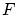 は極大フィルターである.
は極大フィルターである.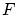 は超フィルターである.
は超フィルターである.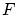 は素フィルターである.
は素フィルターである.
(命題終わり)
- (*6)
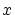 を
を  上の真のフィルターとするとき
上の真のフィルターとするとき
- (*6の証明)
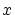 を
を  上の真のフィルターとし,
上の真のフィルターとし, 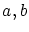 を任意にとる.
を任意にとる.
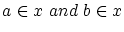 なら (F2) により
なら (F2) により
逆に
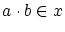 なら (*2) から
なら (*2) から
で (F1) により
(*6の証明終り)
- (*7)
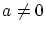 とすると
とすると
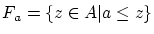 は真のフィルター
は真のフィルター
- (*7の証明)
- (F1)
-
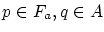 を任意にとり,
を任意にとり, 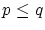 とすると
とすると
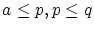 から
から 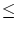 が順序関係なので(*1)
が順序関係なので(*1)
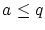 で
で
よって
- (F2)
-
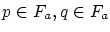 を任意にとると
を任意にとると
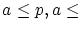 から
から
で
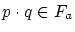 よって
よって
- (F3)
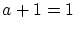 から
から
よって
- (F4)
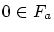 とすると
とすると
また 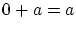 から
から
で結局 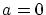 となって矛盾.
となって矛盾.
(*7の証明終)
- (*8)
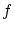 を
を  上の真のフィルターとし,
上の真のフィルターとし,
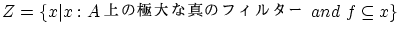 とおくとき
とおくとき
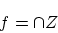
- (*8の証明)
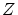 の定義より任意の
の定義より任意の 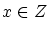 について
について 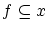 だから
だから
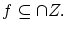
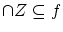 を示すため,
を示すため,
を示す.
( 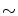 は
は 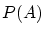 上で)
上で) 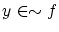 とすると
とすると
- (証明)
- これを否定した
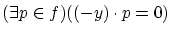 を仮定すると,
これを充たす
を仮定すると,
これを充たす 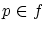 を選んで,
を選んで,
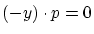 よって
よって
これから, 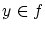 となり矛盾
となり矛盾
(証明終)
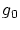 を
を
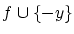 の元の有限個の積全体
の元の有限個の積全体
とおき,
とすると, 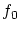 は
は  上の真のフィルターで,
上の真のフィルターで,
- (証明)
- まず,
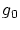 の定義式中,
の定義式中,
とおけば 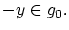 そこで
そこで 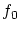 の定義式中,
の定義式中, 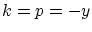 と置けば,
と置けば,
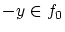 以下,
以下, 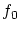 が
が  上の真のフィルタであることを示す.
上の真のフィルタであることを示す.
- (F1)
-
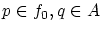 を任意にとり
を任意にとり 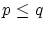 とすると
とすると
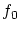 の定義から
の定義から
このような 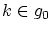 を選び,
を選び, 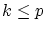 とすると
とすると 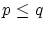 から
から
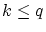 よって
よって 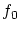 の定義から
の定義から
- (F2)
-
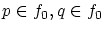 を任意にとると
を任意にとると 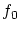 の定義から
の定義から
このような 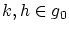 を選び,
を選び,
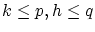 とすると
(*2から)
とすると
(*2から)
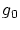 の定義から
の定義から
このような
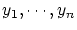 と
と
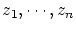 を選べば
を選べば
よって
よって 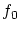 の定義から
の定義から
- (F3)
- まず,
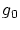 の定義式中,
の定義式中, 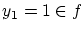 とおけば
とおけば
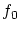 の定義式中,
の定義式中, 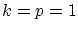 と置けば,
と置けば,
- (F4)
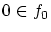 とすると
とすると 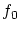 の定義から
の定義から
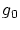 の定義から
の定義から
このような
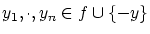 をとると
をとると
よって
ここで
であるから
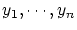 の中で
の中で 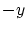 と等しいものがあると矛盾する.
従って,
と等しいものがあると矛盾する.
従って,
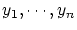 は全て
は全て 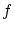 の元
の元
しかしこれから
となって矛盾.
(証明終)
よって 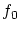 は
は  上の真のフィルターで,
上の真のフィルターで, 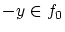
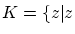 は
は  上の真のフィルター
上の真のフィルター
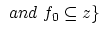 とおくと
とおくと 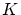 は順序
は順序 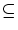 について帰納的順序集合で
について帰納的順序集合で
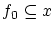 となる極大な真のフィルター
となる極大な真のフィルター 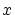 が存在.
が存在.
- (証明)
- 前節の解答「
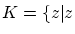 は
は  上の真のフィルター
上の真のフィルター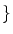 が順序
が順序
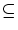 について帰納的順序集合」と殆ど同じなので、違うところだけ
書きます.
について帰納的順序集合」と殆ど同じなので、違うところだけ
書きます.
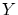 が
が 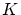 の空でない全順序部分集合なら
の空でない全順序部分集合なら 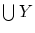 が
が  上の真のフィル
ターで,
上の真のフィル
ターで,
であることは全く同じで,
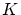 の定義と
の定義と 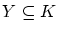 から
から
で
よって
で 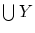 は
は 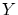 の
の 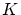 上での
上界
上での
上界
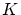 の空でない任意の全順序部分集合が
の空でない任意の全順序部分集合が 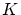 上での上界をもつから
上での上界をもつから 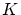 は
順序
は
順序 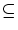 について帰納的
について帰納的
(証明終)
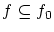 であるから
であるから 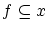 であることに注意して
Zornの補題からKの極大元xが存在.これは
であることに注意して
Zornの補題からKの極大元xが存在.これは
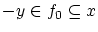 を充たしている.
xは極大なので、
を充たしている.
xは極大なので、
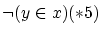 よって
よって
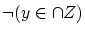 すなわち
すなわち
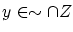 (*8の証明終)
(*8の証明終)
- (*9)
-
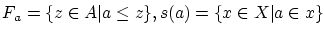 について:
について:
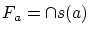
- (*9の証明)
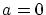 のときは
のときは
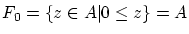
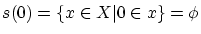 で、
で、
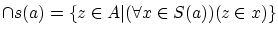 から
から
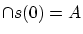 よって
よって 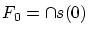 .
.
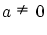 のとき(*7)から
のとき(*7)から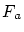 は
は 上の真のフィルターで
上の真のフィルターで
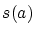 は
は
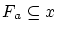 となる
となる 上
の極大な真のフィルターx全体の集合と等しい.
上
の極大な真のフィルターx全体の集合と等しい.
- (証明)
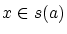 のとき
のとき
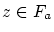 を任意にとると
を任意にとると
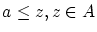
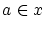 ゆえ (F1)により
ゆえ (F1)により 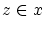
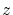 は任意にとったから
は任意にとったから
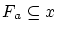 逆に
逆に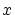 を
を
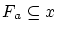 となる
となる 上の
極大な真のフィルターとすると
上の
極大な真のフィルターとすると
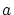 自身
自身 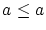 で
で 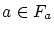 よって
よって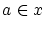 すなわち
すなわち 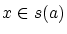 (証明終)
よって、(*8)により
(証明終)
よって、(*8)により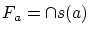
(*9の証明終)
以下
について
- [証明]
- (1)
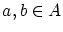 を任意にとり、
を任意にとり、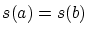 とする.
とする.
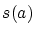 の定義から
の定義から
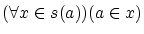 で
で
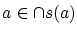
 の定義から
の定義から
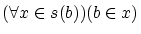 で
で
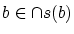 (*9)と仮定から
(*9)と仮定から
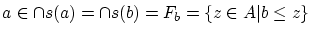 で
で 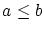 全く同様に
全く同様に
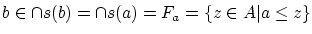 で
で 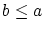 よって
よって 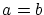
- (2)
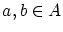 を任意にとり
を任意にとり
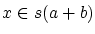 を任意にとると
を任意にとると 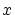 は
は 上の極大な真のフィルターで
上の極大な真のフィルターで
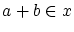 よって(*4)から
よって(*4)から
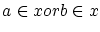 これから
これから
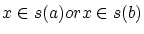 よって
よって
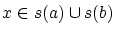
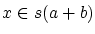 を任意だったから
を任意だったから
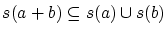 逆に、
逆に、
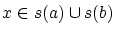 を任意にとると,
を任意にとると,
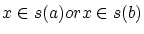 よって
よって
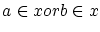 (*2)から
(*2)から
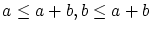 なので
なので
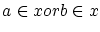 どちらの場合でも
どちらの場合でも 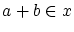 従って、
従って、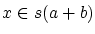
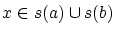 を
任意にとったので
を
任意にとったので
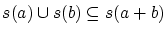 結局、
結局、
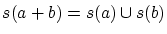
- (3)
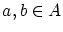 を任意にると
を任意にると
よって
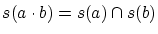
- (4)
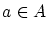 を任意にとると
を任意にとると
よって
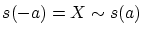 [証明終リ]
[証明終リ]
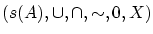 はブール代数です。
はブール代数です。
- [証明]
- これは
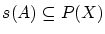 で、今まで何度か出てきましたように
で、今まで何度か出てきましたように
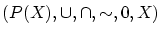 がブール代数ですので、
がブール代数ですので、
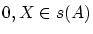 と、
と、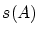 が
が
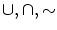 について閉じていることを示せばいいわけです。
について閉じていることを示せばいいわけです。
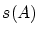 が部分宇宙(部分ブール代数)であることをいえばいいので,
が部分宇宙(部分ブール代数)であることをいえばいいので,
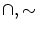 についてのみ閉じていることを示せばいいです.
についてのみ閉じていることを示せばいいです.
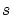 の定義から
の定義から
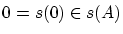 , (左辺の
, (左辺の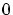 は空集合の意味です。)
は空集合の意味です。)
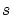 の定義と
の定義と から
から
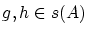 のとき
のとき
でこのような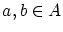 をとれば、
をとれば、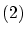 を用いて
を用いて
同様に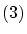 を用いて
を用いて
また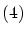 を用いれば
を用いれば
よって、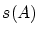 が
が
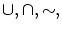 について閉じています。
[証明終]
について閉じています。
[証明終]
既に証明した
(命題)
ブール代数の同型写像の逆写像は,またブール代数の同型写像である.
(命題終わり)
により
 と
と はブール代数の構造について同型。
その同型写像は
はブール代数の構造について同型。
その同型写像は
で定義される。


: この文書について...
: ストーンの同型定理
: 上のブール代数の構造
Yasunari SHIDAMA
![]() がブール代数として、
がブール代数として、 ![]() が
が ![]() 上のブール代数の真の
フィルターというのは
上のブール代数の真の
フィルターというのは
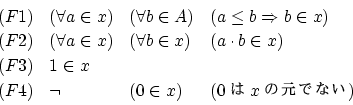
![]() は
は ![]() 上の真のフィルター
上の真のフィルター ![]() は順序「
は順序「 ![]() 」ついて帰納的順序集合
」ついて帰納的順序集合
![]() が
が ![]() 上の真のフィルターだから
上の真のフィルターだから ![]() は順序
は順序 ![]() について 帰納的順序集合なのでZornの補題から
極大な元が存在.
について 帰納的順序集合なのでZornの補題から
極大な元が存在.
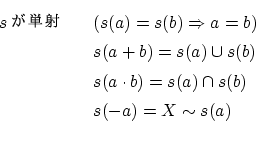
![]() の作り方から
の作り方から ![]() は極大な真のフィルターだったから
は極大な真のフィルターだったから ![]() により
により ![]() となり矛盾
となり矛盾
![]() がいえる真のフィルター
がいえる真のフィルター ![]() を素フィルターといいます.
を素フィルターといいます.
![]() が極大な真のフィルターとするとき
が極大な真のフィルターとするとき
![]() がいえる真のフィルターを超フィルター(ウルトラフィルター)(ultrafilter) と
いいます. 超フィルターは常に
がいえる真のフィルターを超フィルター(ウルトラフィルター)(ultrafilter) と
いいます. 超フィルターは常に ![]() か
か ![]() のどちらか一方のみが
のどちらか一方のみが ![]() の要素と
なるような真のフィルターです.
の要素と
なるような真のフィルターです.
![]() を
を
![]() の元の有限個の積全体
の元の有限個の積全体
![]() の定義から
の定義から
![]() は
は ![]() 上の真のフィルターで,
上の真のフィルターで, ![]()
![]() は
は ![]() 上の真のフィルター
上の真のフィルター
![]() とおくと
とおくと ![]() は順序
は順序 ![]() について帰納的順序集合で
について帰納的順序集合で
![]() となる極大な真のフィルター
となる極大な真のフィルター ![]() が存在.
が存在.
![]() が
が ![]() の空でない全順序部分集合なら
の空でない全順序部分集合なら ![]() が
が ![]() 上の真のフィル
ターで,
上の真のフィル
ターで, ![]() の空でない任意の全順序部分集合が
の空でない任意の全順序部分集合が ![]() 上での上界をもつから
上での上界をもつから ![]() は
順序
は
順序 ![]() について帰納的
について帰納的

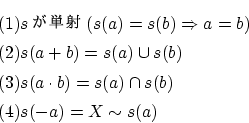


![]() はブール代数です。
はブール代数です。
![]() が部分宇宙(部分ブール代数)であることをいえばいいので,
が部分宇宙(部分ブール代数)であることをいえばいいので,
![]() についてのみ閉じていることを示せばいいです.
についてのみ閉じていることを示せばいいです.
![]() の定義から
の定義から
![]() , (左辺の
, (左辺の![]() は空集合の意味です。)
は空集合の意味です。)
![]() の定義と
の定義と![]() から
から
![]() のとき
のとき