■並行プロセスのモデル化

1.セルオートマトン

2.ペトリネット

3. プロセス代数仕様

参考資料・リンク集

並行動作するプロセスを仕様に基づいて記述し、その動作検証を行うことは重要である。
プロセスのモデル化には、以下のような手法がある。

(1) セルオートマトン（cellular automaton, network automata）
(2) ペトリネット（Petri net）
(3) プロセス代数仕様（BLA : Basic-LOTOS oriented Algebra, CCS, CSP）

●セルオートマトン（cellular automaton）

一つの（有限）状態遷移機械（automata）を「セル（cell）」とし、それをn個定義する。次に、n個のcell_i(i=1,...,n)を協調・同期動作させるための、同期化ラベル積（Synchronized product）を定義する。

1.1 Automataの定義
1.2 Automataの例（modulo 3 counter）
1.3 Execution tree
1.4 Synchronized product の定義
1.5 Cellular automaton の例（ (mod2 x mod3 x mod4) counter）
1.6 minor loopの存在

練習問題1-1

1.1 Automataの定義

A set Prop ={P_1,...} of element propositions (properties) is given. 
An (finite state) automaton is a tuple A = <Q, E, T, q_0, l> in which:


・Q is a finite set of states;
・E is the finite set of transition labels;
・T ⊆ Q x E x Q is the set of transitions;
・q_0 is the initial state of the automaton;
・l is the mapping which associates with each state of Q the finite set
  of elementary properties which hold in that state.

1.2 Automataの例（modulo 3 counter）

Automataの設計例として、mod3カウンタを定義する。
このカウンタは、状態値として {0,1,2}、カウント動作としては増/減に対応するinc/decを有する。
初期状態は 0 とする。
各状態値に対応するatomic propositionは、各々 pr_0, pr_1, pr_2 とする。

・Q = {0, 1, 2};
・E = {inc, dec};
・T = {(0,inc,1), (1,inc,2), (2,inc,0),
       (0,dec,2), (2,dec,1), (1,dec,0)}
・q_0 = 0;
・l = 0 |--> pr_0, 1 |--> pr_1, 2 |--> pr_2.

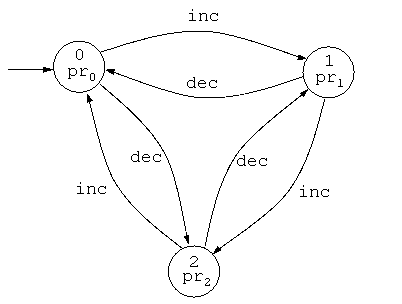
図1.1 state diagram with its atomic propositions of A_c3 : a modulo 3 counter

pr_0, pr_1, pr_2 については、各状態値におけるシステムの「性質」を割り当てる。例えば、各々について、"blue", "yellow", "red" のようなの色（colour）を割り当てる、という風にとらえると理解しやすい。

1.3 Execution tree

mod3カウンタを初期状態から実際に「動作」させ、状態値の遷移を左から順に並べていくことで、そのautomataが取りうる状態空間の探査が行えたことになる。この順列をtree状に表現したものが、Execution tree である。

0
01, 02
012, 020, 010, 021
0120, 0201, 0101, 0212, 0121, 0202, 0102, 0210
.......... 

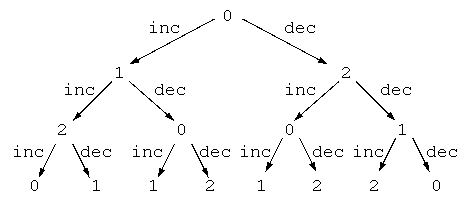
図1.2 Execution tree of A_c3 (after 3 steps)

ここで重要なのは、treeのノード状態値が q であった場合、そこで満足しているシステムの性質は l(q) である点である。すぐに思いつく、このmod3カウンタの性質は以下のようなものが挙げられるであろう。

全てのq∈Qとして、初期状態 0 から開始し、

[P1] 有限ステップ以内には、必ず q に到る
[P2] 現在の状態値が q ==> 次のステップの状態値は q 以外

この性質[P1][P2]のqを用いてl(q)を導くと、各々の性質は、

[P1+] 有限ステップ以内には、必ず blue [yellow,red] になる
[P2+] 現在は blue [yellow,red] ==> 次のステップは blue [yellow,red] 以外

と解釈することができる。

システムのプロパティ形式検証とは、このような[P1+][P2+]の性質が、対象となる定義したautomataの状態空間であるexecution treeを探査することによって、treeの全ての（あるいは一部分の）pathについて満たされているかどうか、についてチェックする一連の操作のことである。

ここで、ステップという時間概念を持つ「性質」を、どのように論理として記述し、検証システムへ反映させるか、という点が実装上のポイントとなる。これについては、従来から modal temporal logic として様々な時相論理系（modal μ-calculus、CTLなど）が提案されている。これについては、後に述べる。

1.4 Synchronized product の定義

Let us consider a family of n-automata,
forall i∈{1,...,n} A_i = <Q_i, E_i, T_i, q_0_i, l_i>.

Now we introduce a new label '-' to represent the the fictitious
action as "do nothing" for any automaton which remains inactive 
during a global transition of set of compositions.

To synchronize the components, we will restrict the transitions
allowed in the cartesian product.

We thus define a synchronization set:
Sync ⊆ Π_{1≦i≦n} (E_i U {-}).

ここで同期化ラベル積 Sync は、1からnまでの各automatonのトランジション間の橋渡しをする積集合の部分集合となっていることが判る。"何もしない"意味の '-' との和をとっているため、automaton間の同期・非同期の選択が可能である。

このSync集合を用いて n個のautomaton : A_1 .. A_n を結合した、cellular automaton : A の定義を以下に示す。

The cartesian product A_1 x ... x A_n of these automata is
simply the automaton A = ＜Q, E, T, q_0, l＞ with:


・Q = Q_1 x ... x Q_n;
・E = Π_{1≦i≦n} (E_i U {-});
・T = { ((q_1,...,q_n),(e_1,...,e_n),(q'_1,...,q'_n))
       | (e_1,...,e_n) ∈ Sync and
         forall i∈{1,...,n} e_i == '-' and q'_i == q_i
                          or e_i <> '-' and (q_i,e_i,q'_i)∈T_i}
・q_0 = (q_0_1, q_0_2, ..., q_0_n);
・l( (q_1,...,q_n) ) = ∪_{1≦i≦n} l_i(q_i).

1.5 Cellular automaton の例（ (mod2 x mod3 x mod4) counter）

Cellular automatonの設計例として、mod2xmod3xmod4カウンタを結合した、3桁幅のカウンタ A_ccc を定義する。（容易に判るように、例えば、mod24xmod60xmod60カウンタを結合すれば、これは秒単位24時間クロックを表すモデルとなるだろう）

mod2, mod4カウンタのautomaton A_c2, A_c4 の定義を以下に与える。mod3カウンタについては先ほど automaton : A_c3 として定義した。

・Q = {0, 1};
・E = {inc, dec};
・T = {(0,inc,1), (1,inc,0), (0,dec,1), (1,dec,0)}
・q_0 = 0;
・l = 0 |--> pr_0, 1 |--> pr_1.

・Q = {0, 1, 2, 3};
・E = {inc, dec};
・T = {(0,inc,1), (1,inc,2), (2,inc,3), (3,inc,0),
       (0,dec,3), (3,dec,2), (2,dec,1), (1,dec,0)}
・q_0 = 0;
・l = 0 |--> pr_0, 1 |--> pr_1, 2 |--> pr_2, 3 |--> pr_3.

新たな性質 pr_3 については、例えば、"black"（colour）などを割り当てておこう。

これら3つのautomaton : (A_1, A_2, A_3) = (A_c2, A_c3, A_c4) を定義に基づいて、まず次のように結合する。この定義では、まだ、同期化ラベル積Syncは空集合であるため、「協調動作しない」。

A_c2 x A_c3 x A_c4 without Sync is defined as:


A_ccc = ＜Q, E, T, q_0, l＞ with:
・Q = Q_1 x Q_2 x Q_3;
・E = Π_{i<=i<=3} (E_i U {-});
・T = { ((q_1,q_2,q_3),(e_1,e_2,e_n),(q'_1,q'_2,q'_3))
       | forall i∈{1,2,3} e_i == '-' and q'_i == q_i}
    = { ((0,0,0),(-,-,-),(0,0,0)), ((0,0,1),(-,-,-),(0,0,1), 
        .... , ((1,2,3),(-,-,-),(1,2,3)) }
・q_0 = (q_0_1, q_0_2, q_0_3);
・l( (q_1,q_2,q_3) ) = l_1(q_1) U l_2(q_2) U l_3(q_3).

Sync無しの場合で、状態空間へ配置した場合の図を以下に示す。状態値の表記は、(Q_1, Q_2, Q_3) である。状態数は、2x3x4=24個となる。

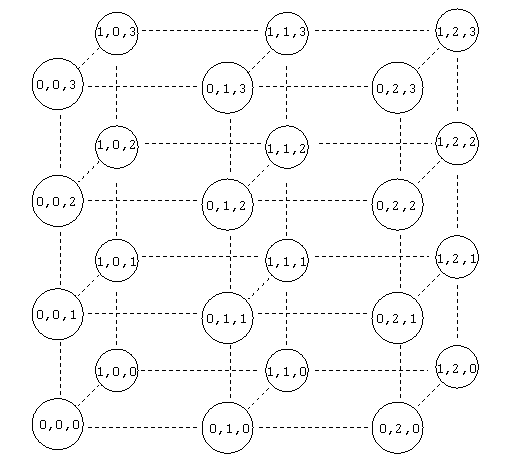
図1.3 The states of the product of the three counters(without Sync) : A_ccc

次に、3つのカウンタを、何らかの意味づけを持たせた上で「協調動作させる」ようなSyncの定義を与えてみる。簡単なSyncの定義は、以下のように、全てのカウンタ値を「一斉に」inc/dec するような同期化ラベル積である。

Sync = {(inc,inc,inc), (dec,dec,dec)}

このSyncを用いて結合した cellular automaton : A^coupl_ccc の動作は、A_cccと比較して、トランジション集合 T が同期化ラベル積の役割により、全体としての遷移が大幅に異なったものとなる。以下の定義では、初期状態 q_0 = (0,0,0) から開始することを前提としている。

A_c2 x A_c3 x A_c4 with Sync is defined as:
A^couple_ccc = ＜Q, E, T, q_0, l＞ with:
・Q = Q_1 x Q_2 x Q_3;
・E = Π_{i<=i<=3} (E_i U {-});
・T = { ((q_1,q_2,q_3),(e_1,e_2,e_n),(q'_1,q'_2,q'_3))
       | forall i∈{1,2,3} e_i == '-' and q'_i == q_i
                        or e_i <> '-' and (q_i,e_i,q'_i)∈T_i}
    = { ((0,0,0),(inc,inc,inc),(1,1,1)), ((1,1,1),(inc,inc,inc),(0,2,2),
        .... , ((1,2,3),(inc,inc,inc),(0,0,0)),
        ((1,0,0),(-,-,-),(1,0,0)), ((1,1,0),(-,-,-),(0,2,2),
        .... , ((0,2,3),(-,-,-),(0,2,3)) }
・q_0 = (q_0_1, q_0_2, q_0_3) = (0,0,0);
・l( (q_1,q_2,q_3) ) = l_1(q_1) U l_2(q_2) U l_3(q_3).

このSyncを用いて結合した cellular automaton : A^coupl_ccc の、初期状態 q_0 = (0,0,0) から到達可能な状態遷移を矢印で結んだ reachable state graph を以下の図に示す。状態(0,0,0)から始まって、12回連続でincした場合、状態(1,2,3)を経て、初期状態(0,0,0)へ戻ってくる（decを12回繰り返しても同様に戻ってくる）。

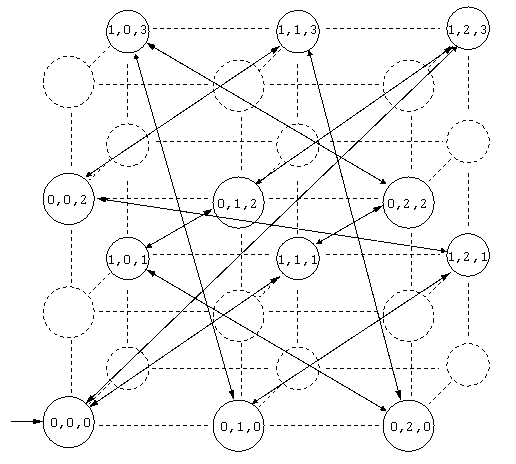
図1.4 The automaton A^coupl_ccc restricted to reachable states

いわんや、これは modulo 12 カウンタと比較し、「観測可能な動作の上において等価（observational equivalent）」のカウンタモデルとなる。なぜなら、結合後の状態遷移(0,0,0)<-->(1,1,1)<--> ... <-->(1,2,3) の各々について、改めて pr_1, pr_2 , ... , pr_12 という色割り当てを行う 写像l が定義されているから。

さて、mod12カウンタの性質については、先ほど例に挙げた mod3カウンタ の色数が増えるだけで、性質[P1+][P2+]について変わりない。つまり、この性質は mod N カウンタに共通した本質である、と言うことができる。この事実が、後で述べるabstract data type を用いたプロパティ検証の有効性の裏付けとなっている。

翻って元の A_ccc の状態数を確認すると、24個の状態が存在していた。このSyncを用いて結合した A^coupl_ccc は、A_ccc で可能性のあった状態空間の「半分（12個）」を用いている。では、状態(1,0,0)など、残りの12個の状態値は、このまま無駄に使われないままなのであろうか？

1.6 minor loopの存在

同期化ラベル積 Sync, 初期状態 q_0 = (0,0,0) によって結合した A^coupl_ccc の状態遷移を判りやすく表現したものを、以下の図に示す。

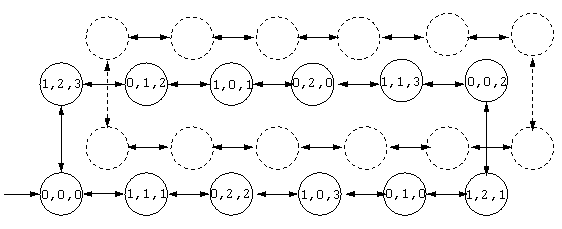
図1.5 The re-arrenged of the state transition graph : A^coupl_ccc

これは、初期状態 (0,0,0) から開始する、mod12カウンタの major loop と見なすことができる。もし仮に、別の初期状態、例えば 状態(1,0,0) から、この結合したautomatonを開始できたとしたら、それは即ち、初期状態 (1,0,0) から開始する、「別の」mod12カウンタである。これを minor loop と呼ぶ。

ここまで見てきた mod12カウンタのmajor loop と mainor loop は本質的に同じシステムモデルである。見なすことができる。初期状態が異なる他は、同期化ラベル積Syncも全て同じな、「別のautomaton」の存在が見て取れる。

強いてこのminor loop のための定義を抜粋して書き下すと、以下のようになる。

・Q = {0, 1};
・E = {inc, dec};
・T = {(0,inc,1), (1,inc,0), (0,dec,1), (1,dec,0)}
・q_0 = 1;

A_c2' x A_c3 x A_c4 with Sync is defined as:


A^couple_ccc' = ＜Q, E, T, q_0, l＞ with:
・Q = ......;
・E = ......;
・T = ......
    = { ((1,0,0),(inc,inc,inc),(0,1,1)), ((0,1,1),(inc,inc,inc),(1,2,2),
        .... , ((0,2,3),(inc,inc,inc),(1,0,0)),
        ((0,0,0),(-,-,-),(0,0,0)), ((1,1,1),(-,-,-),(1,1,1),
        .... , ((1,2,3),(-,-,-),(1,2,3)) }
・q_0 = .... = (1,0,0);
・l( (q_1,q_2,q_3) ) = ...... .

練習問題1-1

[1] mod12カウンタの minor loop : A^coupl_ccc' のための完全な定義を書け。

[2] [1]で定義を書くと、major loop と minor loop の違いが殆ど無いことに気付くであろう。mod2カウンタの トランジション T の定義の「冗長さ」に、"別のautomaton"が発生する要因があるのではないか？（この続きを書け）

[3] mod12カウンタの major loop : A^coupl_ccc は、初期状態 (0,0,0) から開始することを前提としている。もし、この状態機械が（ハードウェアへソフトウェアへの実装において）、何らかの原因で minor loop に含まれるような状態値（例：(1,0,0)）などへ誤って遷移してしまった場合、minor loop から抜け出せなくなってしまう。minor loop からの脱出する方策を考えよ。

[4] 秒単位24時間クロック cellular automaton : A_clock の定義を書け。inc動作のみのmod24,mod60カウンタを結合し、Syncを定義すれば良い。

[5] [4]の定義を少し改良して、AM/PM表示12時間制クロック : A_clock+ の定義を書け。inc動作のみのmod2,mod12,mod60カウンタを結合し、Syncを定義すれば良い。

[6] A_clock(+) には minor loop が無い（当然である）。また、初期状態として何処から開始しても、クロックとしての本質的な性質を満たしている（実際に確かめよ）

●ペトリネット（Petri net）

・並行動作する離散事象システムのモデル化手法の一つ。
・システム資源を表す「プレース」、システムの生成する事象を表す「トランジション」、資源と事象との間の関係を結ぶ「アーク」、ならびにシステム内のデータフローを表現し駆動するための「マーク」から構成される数学モデルである。
・簡単な定義であるため、構造的あるいは動的な、様々な性質について解析性が高い。
・また、各要素を結んだネット図は、視覚的にもシステムの「振る舞い」を理解するための助けになる。

以下では、プレース内のマーク数を複数保有することができる、プレース・トランジション・ペトリネット（p/t-net）について定義を与え、いくつかのモデルの例を示す。

2.1 marked place/transition-net (p/t-net)の定義
2.2 従来のElementary Net Systems と p/t-net との関係
2.3 en-system → 1-safe marked p/t-netのモデル例
2.4 発火条件と次段マーキングのルール
2.5 発火評価順序と可達性
2.6 marking graph
2.7 再び、自販機の例
2.8 諸性質

練習問題1-2

2.1 marked place/transition-net (p/t-net)の定義

A marked place/transition-net (p/t-net) is a tuple N = (P,T,F,k,w,m_0), where


・(P,T,F) is a net with
        P  -  set of places, non-empty, finite
        T  -  set of transitions, non-empty, finite
        F ⊆ (P x T) U (T x P)  -  flow relation
・k : P → {1,2,3,....} U {∞}  -  partial capacity restriction (default:∞)
・w : F → {1,2,3,....}         -  weight function (default:1)
・m_0 : P → {1,2,3,....}       -  initial marking which is satisfying,
                                   forall p∈P, k(p)=∞ and m_0(p)≦k(p)

2.2 従来のElementary Net Systems と p/t-net との関係

p/t-netは、Elementary Net Systems(en-system)を一般化したものである。
全てのen-systemは、1-safe（＝各place内のマーク数が高々１）p/t-netで置き換えられる。

--------------------------------------------------------------
          en-system           1-safe marked p/t-net
--------------------------------------------------------------
             condition   →   place
                 event   →   transition
            case/state   →   marking
         c⊆conditions        m: place P → {0,1}
 sequencial case graph   →   marking graph
                              (reachability graph, state graph)
--------------------------------------------------------------

2.3 en-system → 1-safe marked p/t-netのモデル例

例：自動販売機の制御器（コイン返却機能付き）

このシステムは、
　　(p1)コイン挿入待ち、(p2)コイン判定中、(p3)販売準備OK、
の３つの状態を有する。

発生する事象として、
　　(t1)コイン挿入、(t2)不良コイン返却、(t3)正常コイン受理、(t4)商品販売、
の４つの動作を行う。（同時に高々１つしか事象は発生しない）

システム資源は、挿入された「コイン」ならびに「商品」である。

以下、en-system、1-safe p/t-netでモデル化した例を示す。
2.2で示した変換によって、「並列動作しない」en-systemは、ひとつの 1-safe p/t-net へそのまま置き換えられることを理解しよう。

なお、p/t-netを駆動するための発火評価・次段マーキングのルール、ならびに p/t-netから得られるmarking graphについては、後で定義を与える。

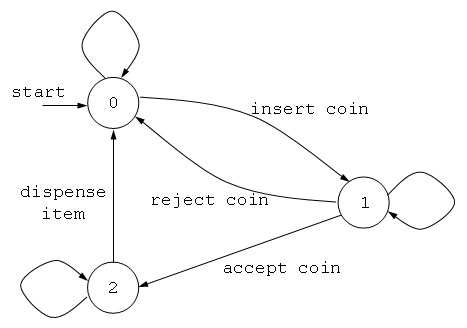
図2.1(a) en-systemでモデル化

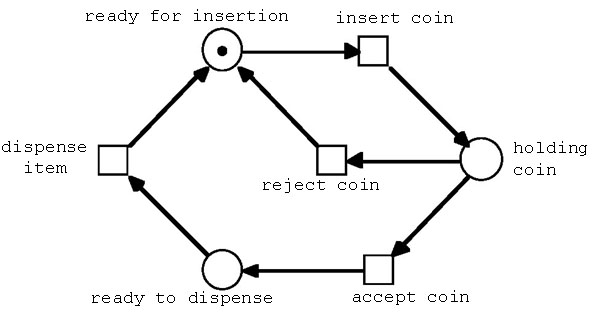
図2.1(b) 1-safe marked p/t-net でモデル化

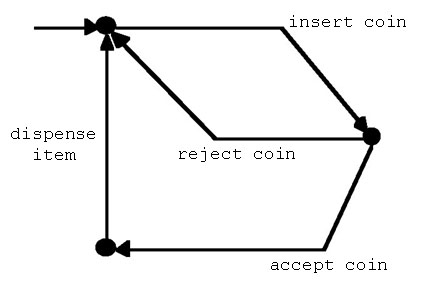
図2.1(c) (b)のbehaviour (marking graph。1.2.5で後述)

2.4 発火条件と次段マーキングのルール

写像 m : P → {0,1,....} を プレース集合Pの marking と呼ぶ。

トランジション t∈T について、次の2つの写像を与える。

*t  : t∈T |--> tの入力プレース集合∈P
 t* : t∈T |--> tの出力プレース集合∈P

トランジションの発火条件についての定義は以下の通り。

A transition t∈T is "enabled" at a marking m, if
  every place p ∈ *t  satisfies m(p) ≧ w(p,t) and
  every place p ∈  t* satisfies m(p) + w(t,p) ≦ k(p).

現在のmarking:mに対して、あるトランジションtについての発火評価を行った後のmarking（次段マーキング）:m'　の定義は以下の通り。（要素に含まれない記号として、!∈ を用いた）

The occurrence of t leads to the successor marking m', defined by


m'(p) =   m(p)                   if p!∈*t and p!∈t*
      or  m(p) - w(p,t)          if p ∈*t and p!∈t*
      or  m(p) + w(t,p)          if p!∈*t and p ∈t*
      or  m(p) - w(p,t) + w(t,p) if p ∈*t and p ∈t* .

tの発火評価に伴うmarking遷移:m→m'（次段マーキング）を、記号 [t> を使って表すこととする。つまり、

m[t>m' ::= m --(t)--> m'

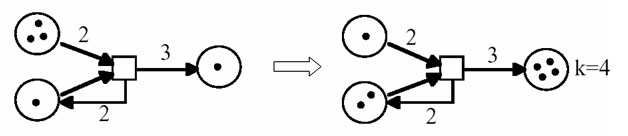
図2.2 あるp/t-netの次段マーキングを行っている様子

2.5 発火評価順序と可達性

トランジション要素 t1, t2, ,,, , tn について、有限順列 σ = t1 t2 ... tn のように並べたものは、「発火評価順序」と呼ぶ。
この順列 σ によって marking m_0, m_1, ..., m_n へ次段マーキングが行われた場合、以下のように書く。

σ : m_0 --(t1)--> m_1 --(t2)--> ... --(tn)--> m_n
あるいは、
σ : m_0 [t1> m_1 [t2> ... [tn> m_n

可達性の定義：

Definition of "a marking is reachable from m_0" :              

marking:m が、初期状態 m_0 から可達（reachable）である
               <=def=> m_0 から m へ到るような、１つ以上の順列σが存在する。

以下の記法を与える。

[m_0> ::= marking m_0 から reachable な 全てのmarking集合。

※長さ無限の発火評価順序　σ' = t1 t2 ..... を考えることもできる。長さが無限だからといって、初期marking:m_0から、全てのmarking集合へ可達であるわけではない（重要）。

2.6 marking graph

marked p/t-net における marking graph とは、初期状態節（initial vertex）から動作させた各状態節（vertices）間をラベル（labeled edges）として方向グラフで結んだものである。可達状態を表したもの。

marking graph の各要素：

initial vertex    - initial marking m_0 (denoted →●)
vertices          - set of reachable markings [m_0>
labeled edges     - set of triples (m,t,m') such that m[t>m'    (m -(t)-> m')

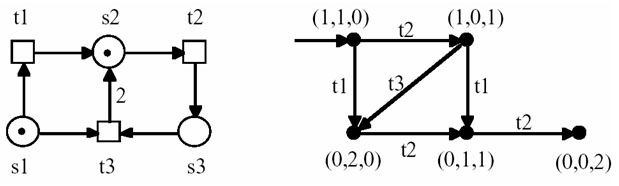
図2.3 p/t-netから生成した marking graph の例

2.7 再び、自販機の例

2.3節にて取り上げた「自動販売機」モデルは、正しいコインが挿入されたら、「商品が無限に出てくる」ような動作仕様になっている。

ここで、このモデルに、商品在庫の資源と補充の動作（storage）を追加する。

まず最初に、「在庫数＝１」のモデルを考える。
具体的には、自販機で商品が販売されて「在庫切れ」状態となったならば、コインを挿入して販売しようとしても、商品が補充されるまで販売を行わない、というモデルとなっている。

並列化としては、自販機の「販売」トランジションを、在庫有り状態に応じて同期化したものとなっている。

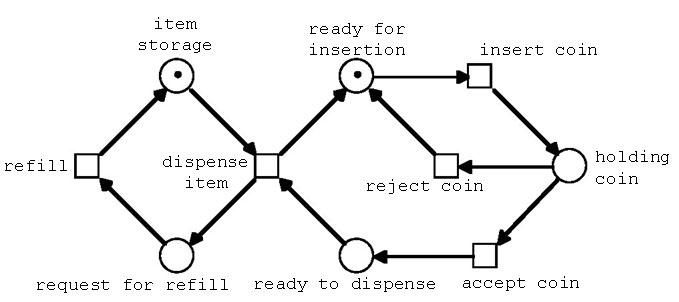
図2.4(a) 自動販売機のモデルその２：在庫数＝１

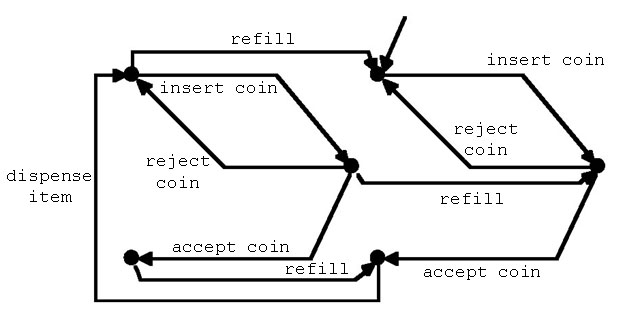
図2.4(b) (a)のmarking graph

在庫数＝４とするためには、ネット構造は変更することなく、初期マーキングのマーク数を１→４に増加させるだけで完了する。

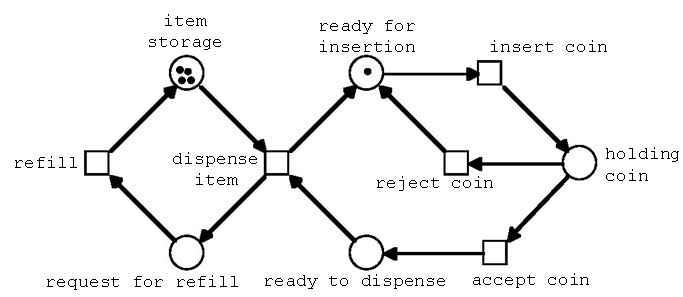
図2.5(a) 自動販売機のモデルその３：在庫数＝４

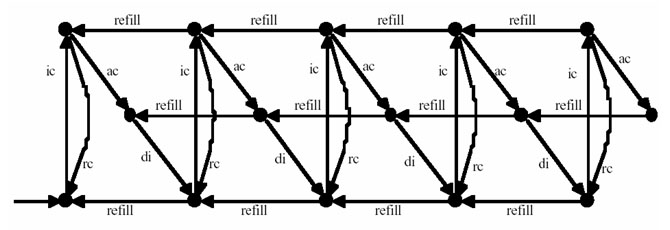
図2.5(b) (a)のmarking graph

ペトリネットにおける上記の事実は、ネットを動作させた振る舞い（動作仕様）が、ネット構造だけでなく、初期マーキングによっても変化することを示している。このことが、構造的性質の解析（p/t-インバリアント解析など）だけでなく、初期マーキングから可達な状態を探査すること（reachability）による動的解析（deadlock-free, boundedなど）を行うことの有意性と、深く関係している。

2.8 諸性質

marked p/t-netに関する（構造的あるいは動的な）主な諸性質は以下の通り。

A marked p/t-net is:

  terminating    - if there is no infinite occurrence sequence

  deadlock-free  - if each reachable marking enables a transition

  live           - if each reachable marking enables
                   an occurrence sequence containing all transitions

  bounded        - if, for each place s, there is a bound B(p)
                   such that m(p)≦B(p) for every reachable marking m

  1-safe         - if B(p) = 1 is a bound for each place p

  reversible     - if m_0 is reachable from each other reachable marking

例：

上記の自動販売機（図2.1(b)、図2.4(a)、図2.5(a)）は何れも、

・deadlock-free かつ live かつ bounded かつ reversible　である。

・terminatingではない（停止しない。noexitの意）。

・図2.5(a)（在庫数４の場合）を除いて、1-safe である。

練習問題1-2

[1] 1.2節で（en-systemによって）定義した modulo 3 counter を、marked p/t-net でモデル化せよ。（inc/dec機能があることに注意）

[2] [1]について、適当な初期マーキングをセットし、marking graph を生成せよ。2.8 の諸性質のうち満足するものはどれか。

[3] 1.5節で定義した、mod2xmod3xmod4カウンタを結合し、以下の同期化ラベル積 Sync によって規定された、mod12カウンタ A^coupl_ccc を、marked p/t-net によってモデル化せよ。Syncの定義と、p/t-netの同期化トランジションとの相似点について考えよ。

[4] [3]について、次の各々の初期マーキングから出発した、marking graph を生成せよ。2.8 の諸性質のうち満足するものはどれか。

(a) 初期状態 q_0 = (0,0,0) から開始
(b) 初期状態 q_0' = (1,0,0) から開始

[5] 例えば、mod 127カウンタを 1-safe marked p/t-net で定義することは、理論上は十分に可能だが、実際のネット定義は大変困難な作業となる。（整数127は素数である）
容量付きプレースと重み付きアークを利用して、marked p/t-net により mod127カウンタのモデル化を試みよ。

[6] [5]について出来上がったネット図は、先の[1][3]などの設計手法・構造的に異なったものとなったであろう。この低記述性の原因は何か。また、どのように marked p/t-net の定義を拡張すると、記述性が改善されるだろうか。

[7] 図2.5(a) 自動販売機のモデルその３：在庫数＝４　について、正しいコインを４つ挿入したら、商品が１つ販売されるように、ネット図を変更せよ。容量付きプレースと重み付きアークを利用してよい。挿入されたコインはプレース内で区別しなくて良い。

[8] [7]のmarking graph を生成せよ。2.8 の諸性質のうち満足するものはどれか。

[9] 自動販売機のモデルについて、商品の種類を３種類（gum, candy, toffee）用意せよ。各々の商品の価格を設定し、コイン挿入後、商品選択が行われたら商品を販売せよ。お釣り返却機能、在庫切れの場合の対応も機能として盛り込むこと。

[10] [9]のmarking graph を生成せよ。2.8 の諸性質のうち満足するものはどれか。

●プロセス代数仕様（BLA : Basic-LOTOS oriented Algebra, CSP）

システムをプロセス（process）の群としてとらえ、相互のメッセージ通信を用いて同期化して全体を構成する方法がある。
プロセスとは、動作（action）の列のことである。動作によって、メッセージを送ったり、受け取ったりする。

各プロセスの定義は、プロセス代数仕様によって行う。
以下、記法としては、Basic-LOTOS oriented Algebra(BLA)を用いる。

LOTOSの process algebraic part については、
CCS : Milner's Calculus of Communicating Systems
CSP : Hoare's Communicating Sequential Processes
に基づいている。並列抽象機械、メッセージ通信によるプロセス定義、についての詳しい知識を欲する場合、これをぜひ読んでおこう。

ここでは、いくつかの例を通して、BLA記法の仕方について見てみる。
正確なプロセス定義と、BLA記法についての諸定義は、次章で行う。

3.1 プロセス定義の例（push button）
3.2 簡単なプロトコル（Simple Protocol）
3.3 Terminating Processes
3.4 Process Graphs
3.5 The Choice Operator
3.6 BLAとPetri net の関係

練習問題1-3

3.1 プロセス定義の例（push button）

電灯の入り切り（on/off）を制御するような「プッシュボタン（push button）」を、プロセス定義によってモデル化する。

プッシュボタンは、'push' という action を行う。
出力として 'on' あるいは 'off' という action を行う。

このプッシュボタンは「故障しない」と仮定する。
また、初期状態（最初の'push'の前）は、'off' であると仮定する。

3.1.1 behaviour expression

上記の仕様に基づいた、プロセス PBL（Push Button Light system）を記述する。
以下、action集合：Act(PBL) = {push, on, off} とする。

PBL = push;on;push;off;push;on;push;off; …

ここで、各actionの逐次的な処理（sequencial processes）を、セミコロン ; で区切って表現した。ここで、最後の記法 … は「永遠に繰返す」ことを期待している。

PBLについては、push->on->push->off をひとつのサイクルとして繰返すから、これをひとまとめにして「永遠に繰返し」たい。

この動作の表現を、*[] と書くことにする。

*[a;b] ::= a;b;a;b;a;b;…

これを用いて、先の … という記法を取り除くと、PBLは以下のように書ける。

PBL = *[push;on;push;off]

3.1.2 recursive equation

他方、PBLは、push->on->push->off の後、PBLプロセスとしての「最初の状態」に戻る、と見ることもできる。故に、4つのactionの次のactionとして、自分自身のプロセス呼び出し PBL を行うように書くこともできる。これを、recursive equation と呼ぶ。

PBL = push;on;push;off;PBL

3.1.3 定理1.1

Law1.1    *[a;b] = a;*[b;a]

上記の定理を利用して、最初に出力を'off'にしてから、規定のサイクルを繰返すようなプロセス：PBL2 を書いてみる。

PBL2 = off;*[push;on;push;off]
     = *[off;push;on;push]      ( <-- by Law1.1 )

3.2 簡単なプロトコル（Simple Protocol）

メッセージ転送を行う簡単なプロトコル（SPROT）についてモデル化を行ってみよう。

3.2.1 SPROTの仕様：

SPROTプロトコルは、2つの送受信プロセス：PSEND, PRECV から構成される。

PSENDは、入力PUTをメッセージ転送チャンネル msg を使って PRECVへ送る。
PRECVは、チャンネル msg から送られてきたメッセージを出力GETとし、ackを返す。
PSENDは、ackを受信したら、次のメッセージ転送手順を開始する。

spec: SPROT

      +---------+   msg    +---------+
      |         |--------->|         |
PUT-->|  PSEND  |          |  PRECV  |-->GET
      |         |<---------|         |
      +---------+   ack    +---------+

        図3.1 Simple Protocol の構成

メッセージ転送チャンネル msg,ack は、必ず正常に動作していると仮定する。

このプロトコルを外から見る（つまり、内部のプロセスPSEND,PRECV間で行われるaction msg,ackで何が行われているかは気にしない（hidden））ならば、SPROTへのPUTとGETのactionの順序（SERVICE）は、常に以下のように行われることが期待されている。

SERVICE = PUT;GET;PUT;GET;… = *[PUT;GET]

3.2.2 PSEND, PRECVの定義と並列化

PSENDは、入力PUTをmsgを使って送信し、ackが返るのを待って、最初に戻る。

PSEND = *[PUT;msg;ack]

PRECVは、msgの受信を待ち、送られてきたら出力GETとし、ackを返し、最初に戻る。

PRECV = *[msg;GET;ack]

図3.1に示すように、2つのプロセスは msg, ack で同期を取りながら、並列動作を行っている。

a,bの2つのプロセスが並列動作することを示す記法 a||b を用いて、PSEND, PRECV を合成した SPROT を書くと以下のようになる。

SPROT =  PSEND || PRECV
      =  *[PUT;msg;ack]
         ||
         *[msg;GET;ack]

3.2.3 SPROTの検証

入力PUTはPRECV側に接続されておらず、出力GETはPSEND側に接続されていないので、これを、後章で見る gated synchronization a|[G]|b を用いて書くと、以下のようになる。

SPROT =  *[PUT;msg;ack]
         |[msg,ack]|
         *[msg;GET;ack]

更にこれを、後章で見る parallel composition に関する諸定理 を用いると、以下が導かれる。

SPROT =  *[PUT;msg;GET;ack]

改めて、このSPROTの内部actionとして msg,ack を外界から見ない（hidden）ものとして扱うと、このSPROTの「外界から観測可能な（observational）」システム動作は、以下のように縮小（reduced）される。

obs. reduced(SPROT) = *[PUT;GET]

2つのプロセス P,Q がobservational equivalence であるとき、これを P==Q と書く。この記法を用いて、

(SPROT == SERVICE) → TRUE

以上のことから、最初に期待したPUTとGETの入出力に関する仕様：SERVICE と、簡単なプロトコルの仕様：SPROT は、observational equivalence （観測可能な状態変化において等価）であること）が示された。

＜追補＞

上記の手法を、model-basedの等価性検証という。可観測な状態値とその振る舞いが仕様としてプロセス表現可能な場合に有効な手法である。しかしながら、各ステップ間での状態値変化を全て仕様として盛り込むことは困難な場合が多く（例：10bitの全加算器の入出力関係を全て列挙するのか？）、また、サイズの大きなモデルの場合、全体のLTS生成（後述）自体が困難なことが多い。このために最近は、仕様をmodal temporal logicで記述し、プロセス定義したモデルからのLTS生成を行った後（あるいは行いながら（on-the-flyという））、記述されたtemporal logicを満足するか否かを、LTSの状態空間探査によってチェックする手法（Model Checkingという）が開発されている。これについては、part2で取り上げる

3.3 Terminating Processes

上記のSPROTの例では、各プロセスともに、永遠に動作を続けることが期待される。

しかしながら、システム仕様によっては、ある動作の列を実行した後、「停止する」ことが必要とされている場合がある。

停止することには、以下の2つの意味がある。

（１）正常に終了する（stop or terminating）
（２）期待に反し、ある状態以降、動かない（stuck or deadlock）

BLAでは、上記の（１）について、記法 $ を用いて　Terminating Processes を表現する。
他方、（２）は解析を行わないと判然としない（参考：Petri net の諸性質）。

プロセスP1が、action a->c の後、"正常に停止する"ことは、以下のように書く。

P1 = a;c;$

プロセスP2が、action b->c の後、"正常に停止する"ことは、以下のように書く。

P2 = b;c;$

例えば、この2つのプロセスP1とP2がaction'c'で同期し並列動作している場合、合成したプロセス P は gated synchronization |[c]| を用いて、次のように書ける。

P  = P1 || P2
   = (a;c;$)
     |[c]|
     (b;c;$)

プロセスPの動作は、a->b->c->stop あるいは、b->a->c->stop のどちらかとなる。また、これ以外の behaviour は、ない。
どちらか一方の behaviour になることは判っているが、どちらかに優先順位があるわけではない。
action a あるいは b の先着順によってどちらかの behaviour が行われる、ということを主張している。
これは、「非決定的動作選択（non-deterministic choice）」と呼ばれる。
C言語などで用いられるif-then-else型の流れ制御は、「決定的動作選択（deterministic choice）」である。

3.4 Process Graphs

Petri net では、トランジション発火評価順序σに基づいた、初期マーキングからの動作状態を marking graph としてトレースし、可達状態の関係を表現した。

プロセスの動作トレースにおいても、同様のグラフ（process graphs）を得る。

            a           b        c
   a;b;c;$ --->  b;c;$ ---> c;$ ---> $

 図3.2 プロセス P = a;b;c;$ の場合の process-graph

automatonやPetri net における「状態」は、プロセスの場合、それ以降実行する「actionの列」で表現する。「状態間のトランジション」としてのラベルは、当然、実行するaction である。

図3.3に、プロセスPBL(=*[push;on;push;off])のprocess graphを示す。
図中の「状態値」{PBL,Q,R,S}は、以下の通り。

PBL ::= push;Q
Q   ::= on;R
R   ::= push;S
S   ::= off;PBL

            push
      PBL -------->  Q
      ↑            ｜
　 off｜            ｜
　　　｜            ｜on
      ｜            ↓
      S <---------  R
            push

 図3.3 PBLのprocess graph

プロセスのbehaviourをトレースした結果のprocess graphから、トランジションラベル付きのautomaton（Labelled Transition System : LTS）を作成することは簡単である。

例えば、先のプロセス P = a;b;c;$ の process graph（図3.2）の場合、これを "automatonとして見る" と、4つのシステム状態値

{s0, s1, s2, s3} = {(a;b;c;$), (b;c;$), (c;$), $} 

が存在することが判る。
トランジション t による状態遷移の記法 [t> を用いて、このプロセスPのLTSは、

s0 [a> s1 [b> s2 [c> s3

と書ける。

プロセスの定義から始まってLTSを生成するまでの、全体の流れを整理すると、以下の通りである。

[step1] プロセスの定義
　↓
[step2] プロセスの合成
　↓
[step3] behaviourのトレース（process graph）
↓
[step4] process graphからLTSを作成（generation）

3.5 The Choice Operator

プロセスにおいて、条件分岐による動作の流れ制御を行いたい時、choice operator を用いる。プロセス P と Q の choice は、P [ ] Q と書く。この選択動作は、非決定的（non-deterministic）である。

P3 = a;b;$ [ ] c;$

このプロセスの動作は、

（１）action 'a' が発生した場合：　a->b->$ の順で実行
（２）action 'c' が発生した場合：　c->$ の順で実行

となる。

プロセス P3 の process graph は以下の通り。

      b        a      c
  $ <--- b;$ <--- P3 ---> $

3.6 BLAとPetri net の関係

ここまで見てきたように、BLAによるプロセス定義（逐次処理、非決定的動作選択、同期化による並列動作）は、そのまま、Petri net により表現が可能であることが判る。

実際、BLAによるプロセス定義について合成を行いLTS生成を行うようなツールの実装では、内部の中間的なトレース動作（トランジションの評価）の実行のために、Petri net を内部で生成して駆動しているものがある。

以下、●：初期マーキングありプレース、○：プレース、|t|：トランジション、-->：アーク　を示している。

Terminology:

      BLA                     Petri net
------------------------------------------------------

     a;b;$     →   ●--->|a|-->○-->|b|-->○-->|$|

    *[a;b]     →   ●--->|a|-->○-->|b|---＋
                    ↑                     ｜
                    ＋---------------------＋

     a;c;$          ●--->|a|-->○-->| |-->○-->|$|
     |[c]|     →                    |c|
     b;c;$          ●--->|b|-->○-->| |-->○-->|$|

     a;b;$           +--->|a|-->○-->|b|-->○-->|$|
     []        →   ●
     c;$             +--->|c|-->○-->|$|

------------------------------------------------------

練習問題1-3

[1] 3.1節で定義した、プロセス PBL（Push Button Light system）のうち、PBL = *[push;on;push;off] は、最初の 'push' action 以前の出力が、on か off のどちらかであるか（どちらであったか）、不明である。このプロセス定義をもとにして、実際の機械、電気回路、あるいはソフトウェアへの実装を行った場合、コントローラとしての初期値が不定なことが、問題になる場合と、ならない場合とがある。このことについて検討せよ。（ヒント：状態をレベルで表現しているか、レベル変化で表現しているか、の違い）

[2] 3.2節で定義した、簡単なプロトコル（SPROT）は、内部のメッセージ転送チャンネル msg, ack について、それらは「故障しない」ことを仮定した。しかしながら、実際の通信路において、絶対に故障しないことは無く、そのような仮定に基づいた検証は意味がない。そのため、プロトコルSPROTについて、メッセージ msg, ack が通過する各々のチャンネルについて、「正常」⇔「一時的な故障」といった状態変化を有するような、MEDIUM1, MEDIUM2 を新たに追加し、新たなプロトコルモデル SPROT2 を作成してみよ。

[3] 1.2節で（en-systemによって）定義した modulo 3 counter を、プロセス定義でモデル化せよ。（inc/dec機能をactionとして実装する）次に、process graph を書け。

[4] プロセス P4 = *[a;b;c] [] *[d;e;f] の process graph を書け。

[5] プロセス P5 = (a;*[b;c]) [] *[d;e;f] の process graph を書け。

[6] 次のような動作を行う自動販売機（Vending Machine : VM）をプロセスで記述せよ。ここで、Act(VM)={coin, gum, candy} である。基本的な動作は次の通り。

　　・自動販売機 VM は、coinを入れると、gum または candy を販売する。
　　・VMは、上記の動作を繰り返し行う。

　　以下の条件(a)あるいは(b)を満たす、VMaあるいはVMbを作成せよ。

　　(VMa) coin挿入後、gum か candy か選択できる。
　　(VMb) coin挿入後、gum か candy か選択できない。どちらを販売するかは、VMbが決める。

[7] 2.7節で定義した、図2.4(a) 自動販売機のモデルその２：在庫数＝１ を、プロセス定義でモデル化せよ。次に、process graph を書け。

[8] 2.7節　図2.5(a) 自動販売機のモデルその２：在庫数＝４　のプロセスによるモデル化は、ここまでで説明したBLAの記法だけでは非常に難しい。なぜならば、現在の「在庫数」を表すメモリをプロセス定義で行うためには、各々の在庫数を表現するような 擬似的なaction （例えば num0, num1, ... , num4 など）を用意した上で、各々の「状態」に応じた choice operation を行う必要があるから。この低記述性を改善するために、BLAについてどのような定義の拡張を行えばよいか。

wasaki@cs.shinshu-u.ac.jp
Copyright(c) Katsumi Wasaki. All rights reserved.