■プロセスと木

1.プロセスの定義

2.プロセス木表現

3. 木の等価性

4. 木の操作

5. 諸定理

練習問題2-1

参考資料・リンク集

プロセスに関する定義を与える。次にプロセスの木表現（Tree）に関する定義を与え、木の等価性について説明する。
更に、選択や逐次接続などの木に対する操作を定義し、それらの操作に関する諸定理を列挙する。

この章で学習する内容は以下の5つである。

1. プロセスの定義（Definitions of Process）
2. プロセス木表現（Process Trees）
3. 木の等価性（Tree Equivalences）
4. 木の操作（Operations on Process Trees）
5. 諸定理（Laws）

練習問題2-1

●プロセスの定義（Definitions of Process）

1.1 定義
1.2 トランジション
1.3 2項関係parent+/child+

1.1 定義

・Des(P) : a finite set of P-descendants (vertex and leaf);

・Act(P) : a finite set of actions (or events) of P,
           not containing the internal action "i";

・ i     : internal, hidden or "non-observable" action;

・Tr(P) ⊆ Des(P) x Act(P)U{i} x Des(P)
         : a transition relation of P.

これらのうち、内部action "i" とは、その解釈として、
　・オートマトン理論におけるε遷移、あるいは
　・CCSにおけるτ(tau)トランジション
であると見做してよい。

1.2 トランジション

Tr(P)の要素は、プロセスPのトランジションである。

例えば、t = <q,a,q'> なるトランジション t があったとしよう。
（アクションaに関して、(parent+)(親/上流)、(child+)(子/下流)という2項関係Rがある）

この時、アクション a によって、プロセス内の状態 q が q' へ移ったことになる。
つまり、
　　t : q --(a)--> q'
である。

これは、前章の記法 [a> を用いて、
　　t : q [a> q'
と書ける。

"通常の終了" である Terminating process $ は以下の通り。

If Des(P) contains an element without children,
this element is denoted either "$" or "stop".

1.3 2項関係parent+/child+

プロセスPの2項関係に関して、以下が成立する。

P (parent+) q  iff  q is an element of Des(P).

child+についても同様である。

前章で概観した、あるプロセスに対する動作をトレースしたグラフ（process graph）とは、上記の定義において、プロセス内の状態である Des(P)の要素 の間を、トランジション Tr(P)の要素で ラベル付きアークとして結んだものである。

（定義はともかく、通常のグラフ表示では、parent, child の状態 p,p' は省略して、Act(P)の要素、あるいは internal action "i" をラベルとして"表示"したアークを描くことが多い）

●プロセス木表現（Process Trees）

前章の1.3節において、BLA記法によるプロセスの定義方法について述べた。
その際、プロセス間の関係を示すいくつかのオペレータについて取り上げた。

それらのオペレータに関する形式的な定義を与えるために、まず、ラベル付き木（labelled tree）について定義する。

2.1 定義
2.2 木表現が可能な必要十分条件
2.3 木表現の例

2.1 定義

Pを、前節の Def-2.1 で行ったプロセスとする。
プロセスPの labelled tree を用いた木表現の定義は、以下の通り。

Let P be a process as Def-2.1. 
T is a tree of process P with set V(T) and Arc(T) as:

V(T)   : set of nodes of T;

Arc(T) : set of arcs of T labelled by elements of Act(T)U{i},
         where Act(T)=Act(P);

r(T)   : the root node of T;

T(v)   : the subtree of T which has v∈V(T) as its root.

あるアクション y∈Act(T)U{i} による遷移はプロセス木 T に関して、1.2節で説明した記法 [y> を用いると、
v,v'∈V(T), labelled arc <v,y,v'>∈Arc(T)であるとき、T(v)[y>T(v') と書ける。

2.2 木表現が可能な必要十分条件

プロセス P の木表現 T(P) の定義が可能である必要十分条件は、以下の通り。

T represents P
iff
There exists a function f : V(T) → onto Des(P), such that:
  (1) f(r(T))= P, 
  (2) T contains a labelled arc <v,y,v'>∈Arc(T)
      iff
      <f(v),y,f(v')> is a transition of P,
  (3) Let f(v)=Q. There exists an one-to-one mappingξbetween
      the children of v∈V(T), and the transitions outgoing from Q.

プロセス木 T(P)の節（node）には、プロセスPの「状態」が関連付けられる。
プロセス木 T(P)の葉（leaf）には、そのchildは無いため、Def.2-1bにより、$ (terminating) あるいは stop が関連付けられる。

2.3 木表現の例

例：プロセス P3 を以下のように定義する。

P3 = a;b;$ [ ] c;$

このプロセスP3の動作は、
（１）action 'a' が発生した場合：　a->b->$ の順で実行
（２）action 'c' が発生した場合：　c->$ の順で実行
となる。

プロセスP3の定義は以下の通り。
・Des(P3) = { P3, b;$, $ };
・Act(P3) = { a, b, c, $ };
・Tr(P3) = { <P3,a,b;$>, <b;$,b,$>, <P3,c,$>};

プロセスP3の木表現 T(P3)の各要素については、以下の通り。

V(T) = { r, v, X1, X2 }; 　　(* r:root, v:node, X1,X2:leaves *)
Arc(T) = { a, b, c, $ };
r(T) = P3;

ここで、Def.2-2bにおける V(T)からDes(P3)の上への写像 f の存在を確かめると、
各々以下のように導かれる。

(1) f(r(T)) = (P3),
(2) Tr(P3) (= Arc(T)) equals to a set of transition of P,
(3) ξ : (v,X1,X2) |--> (a, b, c) is an one-to-one mapping.

従って、以下のような写像 f が存在し かつ 一意であるから、プロセスP3の木表現
T(P3)は実在する。

f(r) = (P3), f(v) = (b;$), f(X1) = f(X2) = ($).

結局、プロセスP3の木表現 T(P3) は、この f を用いて以下のようになる。

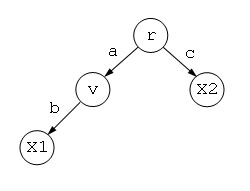
図2.1 プロセスP3の木表現 T(P3)

●木の等価性（Tree Equivalences）

与えられた２つのプロセス木について、様々な条件下における等価性について議論し、挙動の同一性について検討することが多い。

等価性の種類には、主に以下の４つがある。
（１）→（４）の順で、木の等価性に関する条件が緩くなる。

（１）強い挙動の等価性（strongly (strong bisimulation) equivalent）
（２）同型挙動の等価性（branching (stucture bisimulation) equivalent）
（３）部分挙動の等価性（Tau*a-measures equivalent）
（４）観測値での挙動の等価性（observational equivalent）

以下では、これらのうち、(1)strongly equivalent と (4)observational equivalent ついての定義を例にして説明する。

3.1 strongly equivalentの定義
3.2 observational equivalentの定義

3.1 strongly equivalentの定義

P1、P2 を、Def-2.1 に基づいたプロセスとする。
T1、T2 を、Def-2.2aに基づいた P1、P2 のプロセス木 T(P1)、T(P2)とする。

T1、T2がstrongly equivalentであることの定義は、以下の通り。

Let T1 and T2 be process trees with roots r1 and r2, respectively.

The two trees (T1,T2) are strongly equivalent
iff
There exists a relation R between their node sets satisfying
the following conditions (1) -- (3):

(1) r1Rr2 is a relation of each root

(2) There exists a node v2'∈V(T2) such that v2[x>v2'∈Arc(T2) and v1'Rv2',
    whenever v1Rv2 and v1[x>v1'∈Arc(T1).

(3) There exists a node v1'∈V(T1) such that v1[x>v1'∈Arc(T1) and v1'Rv2',
    whenever v1Rv2 and v2[x>v2'∈Arc(T2).

The relation R between tree nodes is called 'bisimulation'.

strongly equivalentであることを、記号 "=" で書く。

２つの木 T1、T2がstrongly equivalentであるならば、２つのプロセスP1、P2はstrongly equivalentである。つまり、

P1=P2 iff T(P1)=T(P2).

例2-1：

次の2つのプロセスP1,P2は、strongly equivalentである。

Process P1 := a;b;$ [ ] a;b;$
Process P2 := a;(b;$ [ ] b;$)

この2つのプロセスP1,P2の関係は、以下のように表すことができる。

(P1 = P2) → TRUE

※これらのプロセスP1,P2は、いずれもbranching equivalent reducing を行うと、P1' := a;b;$ に縮約される。

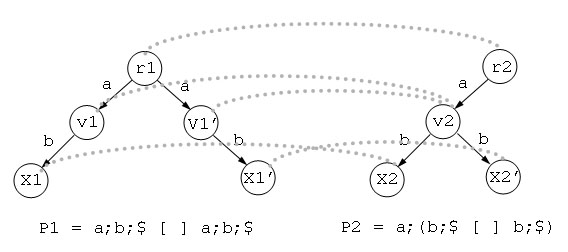
図2.2 プロセスP1,P2の木表現 T(P1),T(P2)

例2-2：

次の2つのプロセスP3,P4は、strongly equivalentである。
'i'は、internal actionである。

Process P3 := a;(b;$ [ ] i;c;$) [ ] a;i;c;$
Process P4 := a;(b;$ [ ] i;c;$)

(P3 = P4) → TRUE

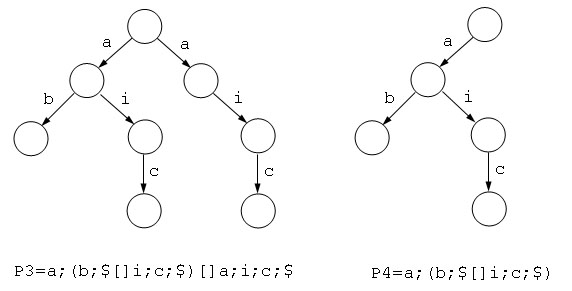
図2.3 プロセスP3,P4の木表現 T(P3),T(P4)

3.2 observational equivalentの定義

先ず、action 'a'の拡張 に関する定義を行う。
この拡張は、ある観測可能な拡張action a とは、その他のactionとともに構成されたシーケンス内に action a が含まれていればよい、とするものである。

Let 'a' be some label.

An extension of 'a' is any sequence in i*ai*,  
where i* denotes a finite (or empty) sequence of i.

We denote v[a>>v’as node v’is reachable from node v
by an extension of a.

ある観測可能な拡張action aに関するobservational equivalentの定義を以下に示す。

P1、P2 を、Def-2.1 に基づいたプロセスとする。
T1、T2 を、Def-2.2aに基づいた P1、P2 のプロセス木 T(P1)、T(P2)とする。

T1、T2が、ある観測可能な拡張action aに関して、observational equivalentであることの定義は、以下の通り。

Let T1 and T2 be process trees with roots r1 and r2, respectively.

Let 'a' be an observable action of one of the processes
represented by T1 and T2.

The two trees (T1,T2) are observational equivalent
iff
There exists a relation R between their node sets satisfying
the conditions (1) - (3) of 'strongly equivalent' (Def-2.3),
with [x> everywhere replaced by [a>>.

Furthermore, we require an additional condition (4) below:

(4) Assume 'i' being the non-observable action,
    and <r1,i,v1>∈Arc(T1) where r1 is a root of T1. 
    Then, T1 may be replaced by T(v1), without affecting
    the conditions Def-2.3 (1)-(3). Similarly, with respect to T2.

observational equivalentであることを、記号 "==" で書く。

２つの木 T1、T2がobservational equivalentであるならば、２つのプロセスP1、P2はobservational equivalentである。つまり、

P1==P2 iff T(P1)==T(P2).

定義から明らかなように、strongly equivalent であるならば、observational equivalentとなる。つまり、

T(P1)=T(P2) ⇒ T(P1)==T(P2).

例2-3：

次の2つのプロセスP1,P2は、観測可能なaction a,b,c について、observational equivalentである。'i'は、internal actionである。

Process P1 := a;(b;$ [ ] i;c;$) [ ] a;c;$
Process P2 := a;(b;$ [ ] i;c;$)

(P1 == P2) → TRUE

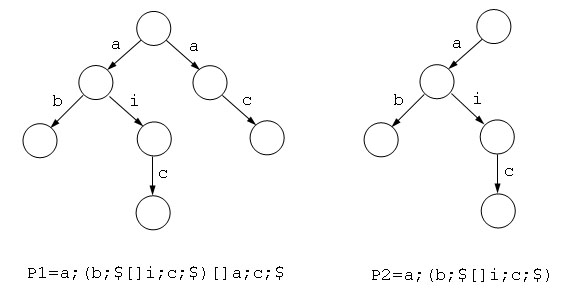
図2.4 プロセスP1,P2の木表現 T(P1),T(P2)

例2-4：

次の2つのプロセスP3,P4は、観測可能なaction a,b,c について、observational equivalentである。

Process P3 := a;(b;$ [ ] c;$)
Process P4 := (a;b;$ [ ] a;c;$)

(P3 == P4) → TRUE

＜付記＞
定義Def-2.5(4)によって 不可観測なaction （例えば internal action 'i'など ）を”取り除いた”プロセス木 T(v1) への変換を、observational reduced tree と呼ぶ。記法としては、( obs. reduced(T1) = T(v1) ) == T1　と書ける。

例えば、例2-3 のプロセスP1,P2のプロセス木T(P1),T(P2)について、T(P1)（or T(P2)）のobservational reduced tree : obs. reduced(T(P1))は、以下のようになる。

obs. reduced(T(P1)) = T( a;(b;$ [ ] c;$) ).

●木の操作（Operations on Process Trees）

プロセス木に対する種々の操作について定義を行う。
定義する操作は、以下の5つである。

----------------------------------------------------------------
name of operation                 usage
----------------------------------------------------------------
Prefixing                         T' = y;T
Choice                            T1 [ ] T2
Spliting                          Y=T;Y --> split Y'=T;Y
Sequential Composition            T1 >> T2
Recursion                         Y = T >> Y
----------------------------------------------------------------

Parallel composition (with gate G) T1|[G]|T2 については、次章で説明する。

4.1 前置操作（Prefixing）
4.2 （非決定的）選択操作（Choice）
4.3 分離操作（Spliting）
4.4 逐次合成（Sequential Composition）
4.5 再帰（Recursion）

4.1 前置操作（Prefixing）

プロセス木 T のroot節の"前"に、プロセス内actionと無関係なラベル y を置いて（prefix）、新たなプロセス木 T'=y;T を合成すること。定義は以下の通り。

Let T be a labelled tree, and y a label not necessarily a label of T.

We define a new labelled tree T'=y:T as follows:

(1) Let w be a node no in V(T).
(2) Add to a new arc <w,y,r>∈Arc(T'), where r is the root of T.

Thus, the new tree T'=y;T is generated evidently to have new root as
r(T') = w.

プロセス木 T(Q)に ラベル y を prefixing した結果の木 T(Q) の関係は、プロセスQに action y を prefixing した結果のプロセスQの関係と、等価である。つまり、

P=y;Q iff T(P)=y;T(Q).

Def-2.6に基づいて、プロセスPの木表現 T(P) は、プロセスQを△で表すと、以下のようになる。node r は、sub-tree Q の root であった。合成後の新たな root node が w となり、トランジション<w,y,r>によって結ばれている。

          y       
      w -----> r -△Q


  図2.5 プロセス P=y;Q の木表現 T(P)

4.2 （非決定的）選択操作（Choice）

P1、P2 を、Def-2.1 に基づいたプロセスとする。
T1、T2 を、Def-2.2aに基づいた P1、P2 のプロセス木 T(P1)、T(P2)とする。

ここで、2つのプロセス木 T1,T2 のroot node : r1,r2 を1つの root node : r にまとめて、新たなプロセス木 T = T1[ ]T2 を合成する操作が、非決定的選択操作（choice）である。記法 [] は、2つのプロセスに対する選択操作の2項演算子である。

2つのプロセス木 T1,T2のchoiceは、2つのプロセスP1,P2のchoiceと、等価である。
つまり、

P1 [ ] P2 iff T(P1) [ ] T(P2).

選択操作による合成後のプロセスPの木表現 T(P) は、プロセスP1,P2を△で表すと、以下のようになる。合成後の新たな root node が r となる。

    P1△--- r ---△P2


  図2.6 プロセス P=P1 [ ] P2 の木表現 T(P)

4.3 分離操作（Spliting）

Process Graph Transformationともいう。
プロセス木 T(P) が、"ラベルP"自体の incoming arc （つまり、プロセスの最初に戻るようなループを持つようなプロセス）を有すると仮定する。

このとき、T(P) を、再帰プロセスを有しないような プロセス木 T'(P) へ、以下の手順で分離することができる。

(1) split the start node of T(P) into two, labelled by P' and P".
(2) connect all arcs incoming to P in T(P) to P" in T'(P).
(3) connect all arcs outgoing from P in T(P) to P' in T'(P)
    as well as to P" in T'(P).
(4) consider the node labelled P' in T'(P) as start node of a 
    process graph T(P').

T(P)とT'(P)は、strongly equivalentである。

例2-5：

前章で定義した、push button process (PBL) は、push;on;push;offのサイクルを繰り返すようなプロセス定義がなされている。

PBL := push;on;push;off;PBL

上記の変換手順に従って、incoming arc : <(off;PBL), off, PBL>∈Arc(PBL)の戻り先ラベル PBL を PBL' とに分離して、新たなプロセス定義 PBL' を定義すると、以下のようになる。

PBL' := push;on;push;off;PBL

4.4 逐次合成（Sequential Composition）

T1、T2 を、2つのプロセスP1、P2 のプロセス木 T(P1)、T(P2)とする。
ここで、T1は有限でかつSTOP節を有しない木とする。
（finite and deadlock-free labelled trees という）

このとき、プロセス木 T1の全てのleaf（葉）に、T2のroot node を接続して木を合成する操作 T1>>T2 が、逐次合成（Sequential Composition）である。

つまり、プロセスP1 の全てのterminating（記法 $ ）の後、プロセスP2が開始される。

例2-6：

Process P1 := coin;(candy;$ [ ] toffee;$)
Process P2 := dispence;$

とする。action : coin, candy, toffee, dispence は、各々、コイン挿入、キャンディ選択、トフィー選択、商品販売、を意味する。

この2つのプロセスを逐次合成して、coinが挿入されて、candy または toffee を1回だけ販売するような、自販機VM1を定義しよう。

この2つのプロセス P1,P2の Sequential Composition : VM1 = P1>>P2 は、以下のようになる。

VM1 = P1>>P2
    = (coin;(candy;$ [ ] toffee;$)) >> (dispence;$)
    =  coin;(candy;dispence;$ [ ] toffee;dispence;$)

＜注意点＞
T1がdeadlock-freeな木で"ない"場合、逐次合成を行おうにも、T1側にterminating $ な leafが存在しないため、T2を接続することができない。
この場合、プロセス木 T = T1>>T2 = T1 となり、逐次処理が為されない（T1側がdeadlockであるので、当然である）。

4.5 再帰（Recursion）

TをプロセスPのプロセス木 T(P)とする。
ここで、Tは non-trivial（$だけの木ではない）かつ、STOP節を有しない（deadlock-free）木とする。

Yをラベルとして、上記4.4のSequential Compositionを用いて、Y = T>>Y なる"合成"をおこなうことが、再帰（Recursion）である。

つまり、プロセスP の全てのterminating（記法 $ ）の後、ラベルY、つまりTの最初に戻る再帰プロセスが形成される。

前章のBLA記法で見た通り、プロセスPを"永遠に繰り返す"ことを *P で表した。つまり、
*P=Q iff *T(P)=T(Q).

＜記法上の注意点＞

アクションa-->b-->a-->…のように"永遠に繰り返す"場合、BLA記法では *[a;b] のように表現し、terminating $ は書かない。プロセス木における上記の合成を意識して書くならば、leaf X に鑑み、*[a;b] は *(a;b;X) とすべきであるが、通常は leaf は陽に書かない。

例2-7：

Process P1 := coin;(candy;$ [ ] toffee;$)
Process P2' := dispence; P1

この2つのプロセス P1,P2'の Sequential Composition : VM2 = P1>>P2 は、以下のようになる。ここで、P2'からラベルP1への戻りは、再帰合成後のプロセスVM2の root node ラベル、つまり VM2 となることに注意せよ。

VM2 = P1>>P2'
    = (coin;(candy;$ [ ] toffee;$)) >> (dispence; VM2)
    =  coin;(candy;dispence;VM2 [ ] toffee;dispence;VM2)

後に見る、(Basic/Full-)LOTOSによるプロセス定義では、いくつかの機能単位でプロセスを定義し、プロセスのラベルを用いた再帰的な合成を行い、システム内の「繰り返し動作」を扱うようにする場面が多い。

●諸定理（Laws）

プロセス木に対する諸定理についてまとめる。

strongly equivalentであることを、記号 "=" で書く。
observation equivalentであることを、記号 "==" で書く。

trivialな木（= leafがterminating $ のみで、これがroot node でもある木）は、$で書く。

以下の諸定理の全ては、プロセスPiの木表現Tiと読み替えることで、プロセスPiに関する諸定理として適用できる。

(1) Choice : [ ] に関する諸定理

プロセス木 T,$,T1,T2,T1',T2'について、以下が成立する。

Law 2.1:   T1[ ]T2 = T2[ ]T1

Law 2.2:   (T1[ ]T2)[ ]T3 = T1[ ](T2[ ]T3)

Law 2.3:   T[ ]T = T

Law 2.4:   T[ ]$ = T

Law 2.5    T1 = T1' and T2 = T2'  implies  T1[ ]T2 = T1'[ ]T2'

(2) Sequential Composition : >> に関する諸定理

プロセス木 T1, T2 を、finite and deadlock-free labelled tree とする。
このとき、以下が成立する。

Law 2.6: (T1>>T2)>>T3 = T1>>(T2>>T3)

Law 2.7: (T1[ ]T2)>>T3 = (T1>>T3) [ ] (T2>>T3)

(3) inaction : i に関する諸定理

プロセス木 T、inaction i とする。
このとき、以下が成立する（obs. equivalent であることに注意）。

Law 2.8: a;i;T == a;T

Law 2.9: T [ ] i;T == i;T

練習問題2-1

[1] push buttonモデルのプロセス(PBL)について、その木表現を Def-2.2a に基づいて書け。再帰プロセスであるから、terminatingはない。

[2] 練習問題1-3の自動販売機モデル(VMa,VMb)について、各々のプロセス定義を Def-2.1a に基づいて書け。また、各々の木表現を Def-2.2a に基づいて書け。

[3] 例2-1のプロセス木 T(P1),T(P2) 間の bisimulation R を書け。

[4] 例2-2のプロセス木 T(P3),T(P4) 間の bisimulation R を書け。

[5] 次の2つのプロセスP1,P2が、obs. equivalenceであるか否かを示せ。

Process P1 := i;a;b;$
Process P2 := i;a;b;$ [ ] a;b;$

[6] 次の2つのプロセスP1,P2が、obs. equivalenceであるか否かを示せ。

Process P1 :=i;a;b;$ [ ] b;c;$
Process P2 := a;b;$ [ ] b;c;$

[7] 次の2つのプロセスP1,P2が、obs. equivalenceであるか否かを示せ。

Process P1 := a;(b;$ [ ] i;c;$) [ ] a;c;$
Process P2 := a;(b;$ [ ] i;c;$)

T(P1),T(P2)間の bisimulation R を作成するなかで、Def-2.3の条件に合致しないものは、どの要素か？

[8] 例2-3のプロセス木 T(P1),T(P2)間の action a,b,cの拡張に関するbisimulation R を書け。また、定義Def-2.5の条件(4)を満たしているか、確かめよ。

[9] 例2-4のプロセス木 T(P3),T(P4)を書け。定義Def-2.3に基づいてbisimulation R の作成を試みよ。どのノード間の関係が bisimilarとしての条件の不整合を為しているか。
[10] Law 1.1: [a;b] = a;*[b;a]　を Process Graph Transformation (Def-2.7)
に基づいて証明せよ（ヒント：両辺は、strongly equivalentの関係である）

[11] Law 2.1 〜 2.9 を、各操作と等価性の定義に基づいて証明せよ。

wasaki@cs.shinshu-u.ac.jp
Copyright(c) Katsumi Wasaki. All rights reserved.