


Next: 安定判別
Up: 定常線形系の性質
Previous: 可制御性
状態
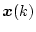 が観測可能な出力信号
が観測可能な出力信号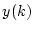 の現在および過去の値から
決定できる場合を可観測という。
の現在および過去の値から
決定できる場合を可観測という。
いま自由系について考えると、
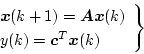 |
(4.115) |
で表した場合
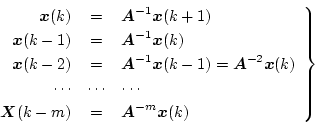 |
(4.116) |
となるので
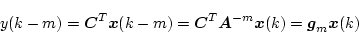 |
(4.117) |
とおくと
![\begin{displaymath}
\left[
\begin{array}{c}
y(k) \\
y(k-1) \\
\vdots \\
...
...oldmath$x$}(k)
\end{array} \right] = \mbox{\boldmath$Gx$}(k)
\end{displaymath}](img269.png) |
(4.118) |
となる。ここに
![\begin{displaymath}
\mbox{\boldmath$G$} =
\left[
\begin{array}{c}
\mbox{\bol...
...\boldmath$C$}^T\mbox{\boldmath$A$}^{-n+1}
\end{array} \right]
\end{displaymath}](img270.png) |
(4.119) |
であり、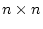 のマトリクスである。もし
のマトリクスである。もし
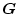 が正則で逆行列が得られるなら
が正則で逆行列が得られるなら
![\begin{displaymath}
\mbox{\boldmath$x$}(k) =
\mbox{\boldmath$G$}^{-1}
\left[
...
...(k) \\
y(k-1) \\
\vdots \\
y(k-n+1)
\end{array} \right]
\end{displaymath}](img273.png) |
(4.120) |
となり、
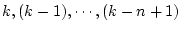 の時点の出力信号
の時点の出力信号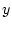 が記憶されているなら
が記憶されているなら
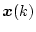 が定められることになり可観測である。
が定められることになり可観測である。
[例]次の離散値系の可観測を検討する。
であるから
ゆえ
これは特異行列ゆえ可観測ではない。
Yasunari SHIDAMA
平成15年6月30日
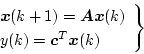
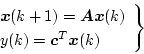
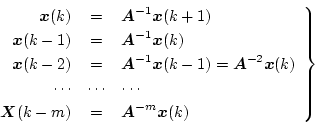
![\begin{displaymath}
\left[
\begin{array}{c}
y(k) \\
y(k-1) \\
\vdots \\
...
...oldmath$x$}(k)
\end{array} \right] = \mbox{\boldmath$Gx$}(k)
\end{displaymath}](img269.png)
![\begin{displaymath}
\mbox{\boldmath$G$} =
\left[
\begin{array}{c}
\mbox{\bol...
...\boldmath$C$}^T\mbox{\boldmath$A$}^{-n+1}
\end{array} \right]
\end{displaymath}](img270.png)
![\begin{displaymath}
\mbox{\boldmath$x$}(k) =
\mbox{\boldmath$G$}^{-1}
\left[
...
...(k) \\
y(k-1) \\
\vdots \\
y(k-n+1)
\end{array} \right]
\end{displaymath}](img273.png)
![\begin{eqnarray*}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array} ...
...ath$C$}^T = \left[ \begin{array}{cc}
3 & 3
\end{array} \right]
\end{eqnarray*}](img276.png)
![\begin{displaymath}
\mbox{\boldmath$A$}^{-1} = \left[ \begin{array}{cc}
-2 & -...
...ght] =
\left[ \begin{array}{cc}
-3 & -3
\end{array} \right]
\end{displaymath}](img277.png)
![\begin{displaymath}
\mbox{\boldmath$G$} = \left[ \begin{array}{cc}
3 & 3 \\
-3 & -3
\end{array} \right]
\end{displaymath}](img278.png)