


Next: 可観測性
Up: 定常線形系の性質
Previous: 任意入力に対する過渡応答
可制御性
システム方程式
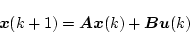 |
(4.109) |
で与えられるシステムが、任意の初期状態
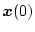 から、任意の希望値
から、任意の希望値
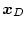 に有限時間で達せられる場合を可制御という。
に有限時間で達せられる場合を可制御という。
いま、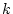 が
が
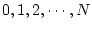 と変化した場合(ただし
と変化した場合(ただし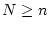 )
)
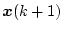 は、
は、
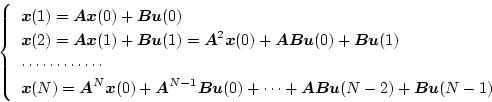 |
(4.110) |
となる。そこでもし
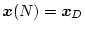 となれば可制御であるといえる。
となれば可制御であるといえる。
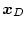 は任意であるから、
は任意であるから、
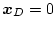 という原点にとると
という原点にとると
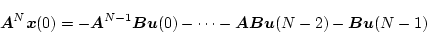 |
(4.111) |
となり、さらに
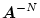 を両辺に掛けると
を両辺に掛けると
ただし
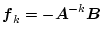
![$ \left[ \mbox{\boldmath$f$}_1\mbox{\boldmath$f$}_2\cdots\mbox{\boldmath$f$}_N \right] $](img255.png) のうち
のうち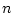 個の
線形独立なベクトルがあれば、任意の初期値から任意の希望値に有限時間で
達せられる。すなわち可制御である。特に
個の
線形独立なベクトルがあれば、任意の初期値から任意の希望値に有限時間で
達せられる。すなわち可制御である。特に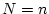 の場合は
の場合は
![$\mbox{\boldmath$F$} = \left[ \mbox{\boldmath$f$}_1\mbox{\boldmath$f$}_2\cdots\mbox{\boldmath$f$}_N \right] $](img258.png) が正則であれば可制
御である。
が正則であれば可制
御である。
[例]システム方程式
![\begin{displaymath}
\left.
\begin{array}{l}
\left[
\begin{array}{c}
\dot{x}...
...}{c}
x_1 \\
x_2
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img259.png) |
(4.113) |
の系を離散値系にしたときの可制御性を検討する。
上式を離散値系の状態方程式で表現すると
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arr...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img260.png) |
(4.114) |
となる。ゆえに
より
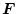 が特異行列ではないので可制御である。
が特異行列ではないので可制御である。
Yasunari SHIDAMA
平成15年6月30日
![]() が
が
![]() と変化した場合(ただし
と変化した場合(ただし![]() )
)
![]() は、
は、
![\begin{displaymath}
\left.
\begin{array}{l}
\left[
\begin{array}{c}
\dot{x}...
...}{c}
x_1 \\
x_2
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img259.png)
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arr...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img260.png)
![\begin{displaymath}
\mbox{\boldmath$A$} =
\left[
\begin{array}{cc}
1 & 0.632...
...gin{array}{cc}
1 & -1.718 \\
0 & 2.718
\end{array} \right]
\end{displaymath}](img261.png)
![\begin{displaymath}
\mbox{\boldmath$f$}_1 = -\mbox{\boldmath$A$}^{-1}\mbox{\bold...
...eft[ \begin{array}{c}
3.617 \\
-4.617
\end{array} \right]
\end{displaymath}](img262.png)
![\begin{displaymath}
\mbox{\boldmath$F$} = \left[ \begin{array}{cc}
0.718 & 3.617 \\
-1.718 & -4.617
\end{array} \right]
\end{displaymath}](img263.png)