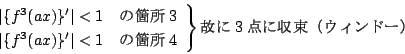

Next: —ЈҺU’lҢnғIғ“ҒEғIғtҗ§Ңд
Up: ”сҗьҢ`—ЈҺU’lҢn
Previous: ”сҗьҢ`—ЈҺU’lҢn
[—б]
”сҗьҢ`ғvғүғ“ғgӮМ“Бҗ«
—ЈҺU’l•ВғӢҒ[ғv“Бҗ«
 |
|
|
|
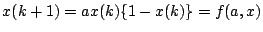 |
|
|
(6.2) |
- (1).
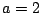 ӮМҸкҚҮ
ӮМҸкҚҮ
Ңр“_ӮЙӮЁӮҜӮйҢXҺО
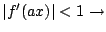 Ңр“_ӮЦҺы‘©
Ңр“_ӮЦҺы‘©
җ} 6.2:
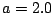 ӮМҸкҚҮ
ӮМҸкҚҮ 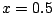 ӮӘ•ҪҚt“_
ӮӘ•ҪҚt“_
|
|
- (2).
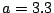 ӮМҸкҚҮ
ӮМҸкҚҮ
Ңр“_ӮЙӮЁӮҜӮйҢXҺО
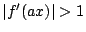
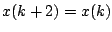 ӮМҢ`ӮЙҺы‘©
ӮМҢ`ӮЙҺы‘©
җ} 6.3:
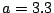 ӮМҸкҚҮ
ӮМҸкҚҮ 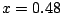 ӮЖ
ӮЖ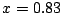 ӮМҠФӮМҗU“®
ӮМҠФӮМҗU“®
|
|
- (3).
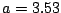 ӮМҸкҚҮ
ӮМҸкҚҮ
Ңр“_ӮЙӮЁӮҜӮйҢXҺО
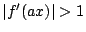
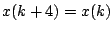 ӮМҢ`ӮЙҺы‘©
ӮМҢ`ӮЙҺы‘©
җ} 6.4:
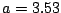 ӮМҸкҚҮ
ӮМҸкҚҮ
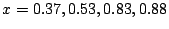 ӮМҗU“®
ӮМҗU“®
|
|
- (4).
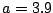 ӮМҸкҚҮ
ӮМҸкҚҮ
Ңр“_ӮЙӮЁӮҜӮйҢXҺО
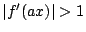
Һы‘©Ӯ№ӮёғJғIғXҢ»ҸЫ
җ} 6.5:
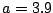 ӮМҸкҚҮ
ӮМҸкҚҮ
|
|
•ӘҠт“_(Bifurcation)
җ} 6.6:
•ӘҠт“_ӮМҸуӢө 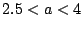 ӮЙ‘ОӮө
ӮЙ‘ОӮө
|
|
Ҡпҗ”ҺьҠъӮМҗU“®
![\begin{displaymath}
x(k+3)=f\{f[f\{a,x(k)\}]\}=f^3(a,x)
\end{displaymath}](img35.png) |
(6.3) |
- (a).
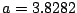 ӮМҸкҚҮ
ӮМҸкҚҮ
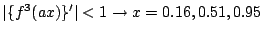 ӮМ3“_ӮЙҺы‘©
ӮМ3“_ӮЙҺы‘©
җ} 6.7:
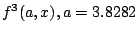 ӮМҸкҚҮ
ӮМҸкҚҮ
|
|
- (b).
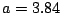 ӮМҸкҚҮ
ӮМҸкҚҮ
җ} 6.8:
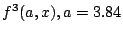 ӮМҸкҚҮ
ӮМҸкҚҮ
|
|
- (c).
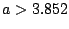 ғJғIғXҸу‘ФҒiғ^ғ“ғWғFғ“ғg•ӘҠт“_Ғj
ғJғIғXҸу‘ФҒiғ^ғ“ғWғFғ“ғg•ӘҠт“_Ғj
3ҺьҠъҗU“®ӮӘ”ӯҗ¶Ӯ·ӮйӮЖӮ«ҒAғJғIғXӮӘ‘¶ҚЭӮ·ӮйҒB


Next: —ЈҺU’lҢnғIғ“ҒEғIғtҗ§Ңд
Up: ”сҗьҢ`—ЈҺU’lҢn
Previous: ”сҗьҢ`—ЈҺU’lҢn
Yasunari SHIDAMA
•Ҫҗ¬15”N8ҢҺ6“ъ
![\includegraphics[scale=0.60]{eps/6-1-1.eps}](img17.png)