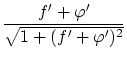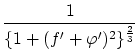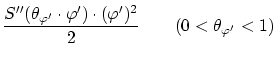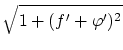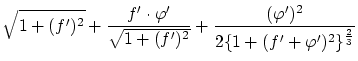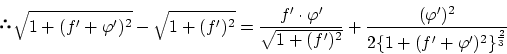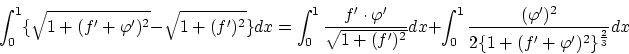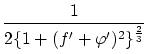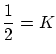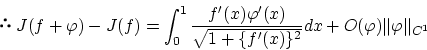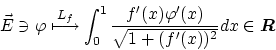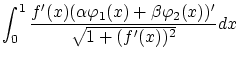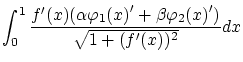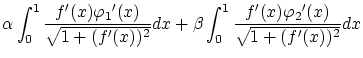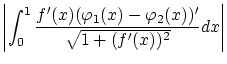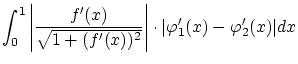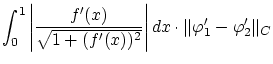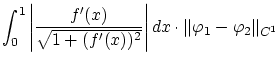


: この文書について...
: 微分
: 微分の定義
目次
ここで,
 微分と第一章で導出した
微分と第一章で導出した
との関係について述べておきます。
この微分は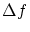 に沿った微分または
に沿った微分または
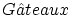 微分と呼ばれます。
微分と呼ばれます。
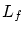 を
を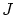 の
の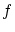 での
での
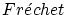 微分とすると,
微分とすると,
であり,両辺を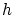 で割って,
で割って,
を得る。
さらに,
ゆえ,
を得る。
これは
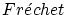 微分可能ならば
微分可能ならば
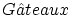 微分可能であり,以下の関係式が成立っていることを示しています。
微分可能であり,以下の関係式が成立っていることを示しています。
問題2の
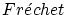 微分
微分
汎関数
の
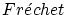 微分を求めてみましょう。
微分を求めてみましょう。
[導出]
ここで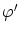 を固定して
を固定して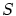 を次のようにします。
を次のようにします。
そして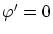 のまわりでテイラー展開を行ないます。
のまわりでテイラー展開を行ないます。
以上より
これらから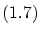 は次のように変形できます。
は次のように変形できます。
ここで
とおくと
したがって
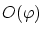 をこのように定義すると
をこのように定義すると
であるので、
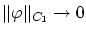 のとき
のとき
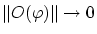
次に線型性を示します。
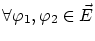 に対して、
に対して、
以上より線型性が示されました。次に連続性を示します。
これを示す
以上より連続性が示されました。



: この文書について...
: 微分
: 微分の定義
目次
Yasunari SHIDAMA
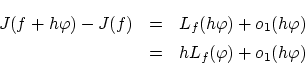
![]() 微分
微分
![]() 微分を求めてみましょう。
微分を求めてみましょう。